Поняття про вимірювання фізичної величини. Класифікація вимірювань

Під вимірюванням фізичної величини розуміють послідовність операцій, які виконуються дослідним шляхом при допомозі технічних засобів(приладів, лабораторних чи технічних установок) спеціально призначених для знаходження з відповідною точністю значення фізичної величини, що характеризує досліджуваний об’єкт або явище.

Всяке вимірювання полягає у порівнянні даної величини з іншою, однорідною величиною, яка взята за одиницю. Але не завжди таке порівняння виконують безпосередньо. У більшості випадків вимірюється не сама величина, а інші величини, які пов’язані з нею тими чи іншими співвідношеннями і закономірностями.

У цьому плані вимірювання поділяють на прямі і непрямі.

До прямих вимірювань належать такі, при яких числове значення шуканої величини отримують в результаті одного відліку чи спостереження. Або прямим називають таке вимірювання фізичної величини, при якому вхідний вимірювальний сигнал вже містить інформацію про вимірювану фізичну величину.

Наприклад: вимірювання температури термометром, атмосферного тиску - барометром, маси – терезами.

При прямому вимірюванні значення фізичної величини отримують за показами вимірюваного приладу.

Непрямі вимірювання – це вимірювання, при яких значення величини, яка являє собою відому функцію інших величин, визначають шляхом обчислень за результатами прямих вимірювань величин – аргументів функції. Потрібно відмітити, що величини, отримані прямими вимірюваннями, вимірюються у відповідних умовах. Тому результат непрямих вимірювань прив’язаний до тих умов, в яких проводились прямі вимірювання.

Широко використовують методи вимірювань, в яких на вхід приладу діє не безпосередньо вимірювання величина, деяка інша фізична величина, яка пов’язана з вимірюваною відомою функціональною залежністю. При цьому для зручності шкалу приладу градуюють в одиницях вимірюваної величини, враховуючи відому функціональну залежність.

Прикладом може бути вимірювання висоти над поверхнею Землі альтиметром, який є барометром. Вимірюваною величиною є висота, а на вхід приладу діє тиск атмосфери. Чи можна вважати такі вимірювання непрямими? Формально так. Але при подібних вимірюваннях немає похибок, які зумовлені обчисленнями. Оскільки результати вимірювань визначаються безпосередньо за показами вимірювальних приладів, їх зручніше віднести до прямих вимірювань.

До непрямих вимірювань відносять тільки такі вимірювання, при яких розрахунок проводять після отримання результатів прямих вимірювань, коли необхідно враховувати окремо похибки обчислень.

Багатократні вимірювання однієї величини виконують для зменшення впливу випадкових похибок вимірювань. Їх відносять до прямих вимірювань, хоча результат цих вимірювань знаходять як середнє арифметичне ряду результатів однократних вимірювань.

Вимірювання поділяють також на лабораторні і технічні.

Лабораторні вимірювання проводять в основному, при різних наукових дослідженнях, коли необхідно забезпечити більш високу точність вимірювань. Для цього під час самого вимірювання і після нього досліджується похибка отриманого конкретного результату вимірювань. Для зменшення можливих похибок результату вимірювань часто використовують такі заходи:

- використовувані засоби вимірювань індивідуально атестуються, визначаються нестабільності їх метрологічних характеристик;

- умови кожного акту вимірювань намагаються зробити такими, щоб нестабільність похибки стала якомога меншою;

- проводять багатократні вимірювання для зменшення впливу випадкових похибок;

- для зменшення динамічної похибки використовують засоби вимірювання з динамічними характеристиками, які за можливістю є близькими до ідеальних (такими, які забезпечують незначну залежність результату вимірювань від швидкості зміни вимірюваної величини.)

Отже, при лабораторних вимірюваннях одночасно проводять два взаємопов’язаних дослідження: одне напрямлене на отримання результату вимірювання з найменш можливою похибкою, а друге на оцінку похибки отриманого результату вимірювання.

Похибка результату лабораторного вимірювання і її характеристики стосуються тільки результату конкретного акту вимірювання. Лабораторні вимірювання вимагають високої кваліфікації персоналу, який проводить вимірювання.

Технічними є вимірювання, для яких наперед визначається певна точність, достатня для даної практичної мети. Це вимірювання, які проводяться в заданих умовах, за певною методикою, розробленою і випробуваною наперед, до проведення вимірювань. Тому при виконанні технічних вимірювань немає потреби визначати і аналізувати похибки отриманих результатів вимірювань. Похибки всіх результатів, які можуть бути допущені при даній регламентованій методиці виконання вимірювань (МВВ) є наперед визначені.

Технічні вимірювання – це, як правило, масові вимірювання. Практично всі вимірювання, які виконують в усіх галузях народного господарства, за винятком наукових досліджень, належать до технічних.

Крім того розрізняють вимірювання постійної, або мало змінюваної фізичної величини, які називають статичними, і вимірювання змінної в часі величини, які називають динамічними.

Взагалі кажучи, незмінність вимірюваних величин, на практиці може зустрічатися лише при цілеспрямованій оцінці постійних похибок, коли вимірювану величину спеціально підтримують незмінною. При практичних вимірюваннях, часто вимірювана величина, повільно чи швидко, але міняється.

При класифікації вимірювань на статичні та динамічні її метою доцільно вважати врахування чи неврахування в конкретних вимірюваннях швидкості зміни величини.

Похибки, зумовлені впливом саме швидкості зміни вимірюваної величини, називаються динамічними. Якщо за певних умов вимірювання (швидкість зміни вимірюваної величини, використовувані засоби вимірювань) динамічною похибкою можна знехтувати - вимірювання статичні.

Сукупні вимірювання – це виконувані одночасно вимірювання кількох однойменних величин, при яких шукані значення величин знаходяться розв’язуванням системи рівнянь, здобутих при прямих вимірюваннях різних сполучень цих величин або при зміні умов вимірювання.

Наприклад6 масу декількох тіл знаходять за відомою масою одного з них, та за результатами прямих порівнянь мас різних сполучень.

Спільні вимірювання – це одночасно виконувані вимірювання двох або кількох неоднойменних величин для знаходження залежності між ними.

Вимірювання може бути виконане за допомогою засобів вимірювання. Це відповідні технічні засоби, які використовуються для і мають нормовані метрологічні властивості.

До засобів вимірювання належать:

1. Міри – це засоби вимірювання, призначені для відтворення фізичної величини заданого розміру (гиря – міра маси). Міри можуть бути однозначними, тобто такими, які відтворюють фізичну величину одного розміру (гиря, нормальний елемент) та багатозначними, що відтворюють однойменні величини різного розміру (лінійка з міліметровими, сантиметровими поділками, конденсатор змінної ємності, магазин опорів). Дуже поширені набори та магазини мір.

2. Вимірювальні прилади – засоби вимірювань, призначені для вироблення сигналу вимірюваної інформації у формі, доступній для безпосереднього сприймання. Вимірювальний прилад, завдяки своїм структурним елементам має: певний принцип дії (фізичний принцип, покладений в основу його будови); вимірювальний механізм, головними складовими частинами якого є чутливий та перетворюючий елемент і відліковий пристрій.

3. Вимірювальні установки – це сукупність функціонально об’єднаних засобів вимірювання (мір, вимірювальних пристроїв, перетворювачів) та допоміжних пристроїв, що призначені для вироблення сигналів вимірюваної інформації у формі, зручній для безпосереднього сприймання.

Залежно від природи вимірюваної величини, будови засобу вимірювання, потрібної точності, зручності і швидкості вимірювання застосовують різні методи вимірювання (сукупність прийомів використання принципів і засобів вимірювання).

- метод безпосередньої оцінки – метод вимірювання, при якому значення величини визначають за відліковим пристроєм вимірювального приладу прямої дії (це прилад, в якому передбачене перетворення (одне чи декілька) одержаної інформації в одному напрямі (без зворотного зв’язку)), манометр, термометр, амперметр;

- метод порівняння з мірою – вимірювану величину порівнюють з величиною відтвореною мірою (зважування на терезах при зрівноважені маси тіла гирями);

- метод протиставляння – це метод, при якому і вимірювана величина і величина, відтворена мірою одночасно впливають на прилад порівняння (знаходження маси на терезах, коли на шальку кладуть і тіло і гирьки);

- диференційований метод – метод порівняння з мірою, коли на прилад впливає різниця вимірюваної величини та відомої величини, яка відтворюється мірою;

- нульовий метод – метод порівняння з мірою, коли результуючий ефект впливу величин на прилад порівняння доводять до нуля (важільні терези, амперметр з нульовою точкою);

- метод заміщення – метод порівняння з мірою, при якому вимірювану величину заміщають відомою величиною, яка відтворюється мірою;

- метод збігів – метод порівняння з мірою, при якому різницю між вимірюваною величиною і величиною, яка відтворюється мірою, знаходять, використовуючи збіг позначок шкали, або періодичних сигналів (ноніус, явище биття, інтерференція, резонанс, стробоскопічний ефект).

Графічне зображення результатів експерименту

В багатьох випадках при обробці результатів фізичного експерименту слід вдаватися до графічного методу, який дає можливість наочніше подавати ре­зультати експерименту — залежність функції у (величина, закономірність якої вивчається) від аргументу х (величина, від зміни якої залежить значення функ­ції), а також графічно знаходити величини у для таких значень х, які безпосе­редньо вимірюванням не досліджувались, наприклад для значення х, проміж­ного між двома вимірюваннями х ₁ і x ₂ (інтерполяція; під інтерполяцією розу­міють, по-перше, знаходження значень функції для проміжних значень аргу­менту х і, по-друге, в чисельному аналізі інтерполяцією називається заміна функції у = f (х) на проміжку [ а, в ] деякою іншою функцією φ (χ), яка в точ­ках х₀, х ₁ ,..., х_n набуває тих самих значень, що й функція у = f (х)).

Мова може йти також про знаходження значень функції у = f (х) для зна­чень аргументу х, менших (або більших), ніж найменше (найбільше) з вимірю­ваних,— екстраполяцією. Звичайно, при цьому має бути тверда впевненість у тому, що характер залежності у = f(х) для областей, де вимірювання не вико­нувались, такий самий, як і в областях, де вимірювання виконувались.

При побудові графіків найчастіше використовують прямокутну систему ко­ординат. Координатні осі використовують як функціональні шкали. Функціо­нальною шкалою називається множина мічених точок, які відображають окремі значення функції та її аргументу. Шкали можуть бути рівномірними і нерівно­мірними. Відстань між двома сусідніми мітками шкали називається графічним інтервалом; різниця цих міток дає ціну поділки. На шкалі, як правило, наносять лише “круглі” мітки. Мітки без підписів називаються німими. Часто німі мітки поділяють проміжок між двома підписаними мітками на деяку кількість рів­них частин.

Носієм функціональної шкали взагалі може бути і деяка крива лінія. Якщо аргумент виражається в кутових одиницях, зручніше використати полярну си­стему координат, а не прямокутну.

Для побудови графіків слід насамперед раціонально вибрати масштаб, тобто щоб на графіку цього розміру (аркуш міліметрового паперу) розмістився весь діапазон експериментальних значень фізичних величин, що їх відкладають на координатних осях, і щоб ціна однієї поділки виражалась, по можливості, ці­лим числом. Одночасно при виборі масштабу слід підпорядковувати точність ви­мірювання точності відліку за графіком. Крім того, слід акцентувати увагу на чіткому вираженні експериментальних даних (експериментальна крива має бу­ти не дуже крутою і не дуже пологою, бо на таких кривих важко робити відлі­ки). Потрібно, по можливості, використати всю площу графіка (якщо дослідні дані величин х і у набагато відрізняються від нуля, відлік поділок потрібно по­чинати на осях з деяких значень, які трохи менші від одержаних під час до­сліду). Після нанесення на функціональні шкали міток біля них пишуть необ­хідні цифри. На кінцях координатних осей (шкал) наносять позначення відкладуваних величин, а одиниці вимірювання їх відокремлюють комою; якщо напис має більше п'яти знаків, то його розміщують вздовж осі, посередині.

Звернемо увагу на те, що числа, знайдені внаслідок вимірювання фізичних величин, є наближеними. Тому замість числа х треба було б писати х ± Δ х, за­мість у — число у ± Δ у. Звідси випливає, що замість точок на графіках треба було б зображати експериментальні дані маленькими прямокутниками з основами 2Δ х і висотами 2Δ у, всередині яких і перебувають справжні дані, знайдені в результаті ідеального експерименту (при цьому авто­матично виділяються також дані різних авторів). Відповідно до цього можна було б провести дві граничні криві, між якими очевидно проходить крива, яка зображує, який насправді вигляд має функція у = f(х).

Під час фізичного практикуму звичайно обмежуються нанесенням точок, а потім за допомогою лекал креслять плавну криву так, щоб вона проходила якомога ближче до всіх експериментальних точок і щоб приблизно однакове число точок було по обидві сторони лінії. Крива повинна, як правило, лежати в ме­жах похибок вимірювання. Чим менші ці похибки, тим краще крива збігається з експериментальними точками.

В основному похибки значень функції більші від похибок аргументу, тому на графіках подають лише похибку функції у вигляді відрізка прямої, довжина якої дорівнює подвоєній похибці у певному масштабі. При цьому експериментальна точка міститься всередині цього відрізка, який з обох кінців обмежується рисками (рис. 1).

Точки перегину, максимуму, мінімуму на експериментальних кривих відповідають якісним змінам у системах, наприклад по­яві нової фази і т. д. У таких точках порушується рівномірність зміни всіх властивостей системи. В областях, близьких до цих син­гулярних точок, слід проводити вимірювання значно частіше. Бу­дуючи графіки плавних залежно­стей, не слід брати багато точок.

Якщо окремі точки значно відхиляються від кривої, то це може свідчити про великі похибки 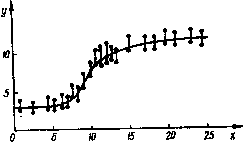вимірювання або явні промахи. Це, в свою чергу, свідчить про потребу підви­щення в цих областях якості вимірювання.

У деяких випадках графічного подання результатів фізичного експеримен­ту доцільно користуватись логарифмічними та напівлогарифмічними функціо­нальними сітками. При цьому слід використовувати друкарським способом зроблений логарифмічний та напівлогарифмічний папір. На логарифмічному папері залежності у = ах^в, а на напівлогарифмічному - залежності у = а^вх зображують прямими лініями. Логарифмічний масштаб зручний при графічному зображенні величин, границі зміни яких становлять кілька порядків.

Досить часто важливим є питання про подання результатів вимірювання в аналітичній формі. Це питання виведення так званих емпіричних формул іно­ді можна розв'язати за допомогою функціональних сіток, на які наносять експериментальні дані. Закон відповідності, на функціональній сітці якого ці дані зображуються практично прямою лінією, придатний для аналітичного описання експериментальної функціональної залежності між фізичними величинами.

Не нашли, что искали? Воспользуйтесь поиском: