Додавання і віднімання наближених значень чисел

Правило 1. При додаванні і відніманні наближених значень чисел, в записі яких всі цифри правильні, залишають стільки десяткових знаків, скільки їх має наближене дане з найменшим числом десяткових знаків.

Приклад. 6,28+13,1+5,462=24,862 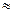24,9.

В результаті зберегли один десятковий знак (за правилом заокруглення).

Хоча абсолютна похибка суми невідома, ми можемо зробити висновок: цифри 2 і 4 правильні, цифра 9 сумнівна. Як бачимо отримана сума 24,9 записана в повному співвідношенні з правилом записування наближених чисел.

Фактично всі рівності в обчисленнях з наближеними значеннями мають наближений характер. Однак для зручності знак наближеної рівності (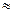) будемо використовувати тільки в тих випадках, коли проводиться заокруглення. Тоді коли дія виконується формально точно, будемо умовно використовувати знак точна рівність (=).

Задача 1. Знайдіть рівнодійну шести сил, що діють на одну точку вздовж однієї прямої і в одному напрямку, якщо F₁=2,81 Н, F₂=3,35 Н, F₃=4,48 Н, F₄=5,04 Н, F₅=6,50 Н, F₆=7,34 Н.

Розв’язок: R=2,81+3,35+4,48+5,04+6,50+7,34=29,52 Н

Правило 1 можна застосовувати тоді, коли число доданків порівняно невелика (не більше 12). У фізичних задачах маємо справу з невеликим числом доданків, і тому це правило завжди застосовне.

Задача 2. Електричне коло складається з лампи опором 305 Ом і з’єднувальних проводів опором 0,37 Ом. Знайдіть загальний опір кола.

Розв’язок. R=305+0,37=305,37 Ом 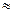305 Ом.

Правила наближених обчислень показали, що при визначенні загального опору подібного кола опір проводів можна не враховувати. Вчителю фізики необхідно звернути увагу учнів на це, підкреслити, що правила наближених обчислень допомагають в деяких випадках вирішити питання чисто фізичного змісту.

Деякі труднощі можуть виникнути при додаванні цілих чисел, які задані з різною точністю. Розглянемо приклад: знайдіть суму наближених значень чисел, записаних у стандартній формі:

х=2,740^.10⁵+2,14^.10⁴+8,6^.10⁶.

Найпростіше це зробити так: винести множник 10 в найбільшому степені (в даному випадку 10⁶) за дужки: х=10^6.(0,2740+0,0214+8,6)=10^6.8,8954 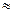8,9^·10⁶.

При додаванні і відніманні наближених значень чисел, число значущих цифр результату може деколи відрізнятися від числа значущих цифр вихідних даних. Розглянемо це на прикладі задачі.

Задача 3. Дві сили 0,860 і 0,855 Н, прикладені до однієї точки тіла, діють на одній прямій. Знайдіть рівнодійну, якщо сили напрямлені в одну сторону; в протилежні сторони.

Розв’язування: R₁=0,860+0,855=1,715 Н, R₂=0,860-0,855=0,005 Н.

В першому випадку по числу значущих цифр відповідь точніша вихідних даних, тобто отримали “підвищення точності”; в другому випадку відповідь менш точна ніж вихідні дані, тобто відбулось “зниження точності”.

При різниці близьких чисел відбувається “зменшення точності”. Це явище у фізичних задачах зустрічається при застосуванні формул, які містять різницю величин, наприклад: , , 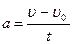і ін.

Крім того, зі “зниженням точності” ми зустрічаємось при вимірюваннях в лабораторних роботах.

Щоб цього не було, необхідно вибирати компоненти різниці так, щоб вони не були числами, близькими один до одного. В окремих випадках можна уникнути ”зменшення точності” шляхом алгебраїчних перетворень.

Не нашли, что искали? Воспользуйтесь поиском: