Піднесення до степеня і добування кореня

З піднесенням до степеня і добування кореня при більш високих показниках ми маємо справу порівняно рідко. Тому правила підрахунку цифр для цих дій формулюються лише для піднесення до квадрата і куба, а також для добування квадратного і кубічного кореня.

Правило 3. При піднесенні до квадрата і куба потрібно зберігати в результаті стільки значущих цифр, скільки правильних значущих цифр має наближене значення числа, що підноситься до степеня.

Наприклад, 1,6²=2,56 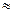2,6. Так як число 1,6 має дві значущі цифри, то і степінь повинен мати дві значущі цифри.

Розглянемо задачу, в якій застосовується піднесення до квадрата наближеного значення числа.

Задача 9. У скільки разів збільшиться кількість теплоти, що виділяється електронагрівачем, при збільшенні сили струму в 1,5 рази? В 2,0 рази? В 4 рази?

Розв’язування. Так, як кількість теплоти прямо пропорційна квадрату сили струму, то:

n₁=1,5²=2,25 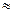2,3 рази; n₂=2,0²=4,0 рази; n₃=4²=16 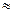20 раз.

В останньому приладі нуль в кінці числа незначуща цифра. Тому в даному випадку відповідь краще сформулювати так: кількість теплоти збільшиться приблизно в 20 раз (а не в 16 раз, як це було б при точному значенні 4).

Аналогічно застосовується правило 3 для піднесення наближеного значення числа в куб. Наприклад: 2,1³=9,261 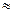9,3.

Потрібно мати на увазі, що при обчисленні куба похибка перевищує похибку квадрата, тому остання цифра результату є менш надійною.

Розглянемо добування кореня із наближеного значення.

Правило 4. При добуванні квадратного і кубічного кореня потрібно брати в результаті стільки значущих цифр, скільки їх має підкореневе наближене значення числа.

Задача 10. В скільки разів збільшиться період коливань маятника, якщо його довжину збільшити в 3,2 рази? 4,3 рази? 8,0 рази? 16 раз? Задані значення вважати наближеними.

Розв’язування. Період коливань маятника пропорційний квадратному кореню із довжини маятника, тому: n= рази; n= 2,1 рази; n= 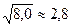рази; n= 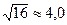рази.

Останній результат пояснимо. Так, як число 16 має дві значущі цифри, то і 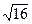повинен за правилом 4 мати дві значущі цифри, тому 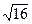=4,0, а не 4.

Результати, отримані за правилом 4, виявляються більш надійними, ніж результати піднесення до степеня. Більш того, остання цифра квадратного і кубічного кореня більш надійна, ніж остання цифра заданого підкореневого числа.

Не нашли, что искали? Воспользуйтесь поиском: