Правило обчислень з наперед заданою точністю

В усіх раніше розглянутих правилах підрахунку цифр було встановлено, яку точність результату можна отримати, маючи вихідні дані з деякою точністю.

Не менш цікавою, особливо для фізики, є зворотна задача: з якою точністю потрібно взяти вихідні дані, щоб отримати результат з наперед заданою точністю? Відповідь на це питання дає наступне правило.

Правило 7. Якщо кінцевий результат потрібно отримати з деякою наперед заданою точністю, а дані можна брати з довільною точністю, то в цих даних слід брати по стільки цифр, скільки потрібно для отримання результату з однією зайвою цифрою. В кінцевому результаті ця зайва цифра округлюється.

Іншими словами, щоб при додаванні і відніманні наближених значень чисел отримати результат з точністю до одиниці деякого розряду, потрібно компоненти цих дій взяти з точністю на один розряд більше.

Що стосується інших дій, то для отримання результату з n значущими цифрами компоненти потрібно взяти з n+1 значущою цифрою. В кінцевому результаті зайву цифру відкидають за правилом заокруглення.

Розглянемо застосування правила 7 на прикладі.

Приклад.

Обчислити суму чисел 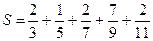з точністю до сотих.

Щоб отримати в сумі два десяткових знаки, беремо в кожному доданку три знаки після коми

.

Легко перевірити, що, взявши доданки з двома десятковими знаками, ми отримаємо інший, менш точний результат:

Не нашли, что искали? Воспользуйтесь поиском: