Наближене обчислення з допомогою мікрокалькуляторів

Існують різні типи мікрокалькуляторів, наприклад, мікрокалькулятори, які виконують арифметичні дії над цілими числами і десятковими дробами, також виконують дії піднесення до степеня і добування кореня, операції з процентами.

Для більш складних обчислень застосовують мікрокалькулятори, з допомогою яких можна не тільки виконувати дії, перераховані вище, але й отримувати значення логарифмів. Він також дозволяє швидко знаходити значення показникової, тригонометричних і обернених тригонометричних функцій, переводити градусну міру кута в радіанну і навпаки, та ін.

Мікрокалькулятори можуть бути використані в школі не тільки при вивченні методів обчислень, але і при розв’язуванні задач на уроках фізики і математики, а також при обробці результатів лабораторних робіт.

Всі операції мікрокалькулятори виконують дуже швидко. Тому тут немає значення невелика раціоналізація обчислювальної роботи, яка досягається застосуванням правила підрахунку цифр при звичайних обчисленнях. За цією причиною повністю відпадає необхідність попереднього заокруглення більш точних даних.

Виникає питання, чи потрібне взагалі правило підрахунку цифр при обчисленнях на мікрокалькуляторах? Так, потрібні, так як правила підрахунку цифр крім функції раціоналізації обчислень, виконують ще одну, більш важливу функцію: дозволяють отримувати результат з точністю, що відповідає точності вихідних даних. Мікрокалькулятори дають результат або точний, або з точністю у 8 знаків, яка може і не відповідати точності вихідних даних. Наприклад, мікрокалькулятор при добуванні квадратного кореня з наближеного значення 2,93 дає:

.

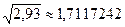Так, як корінь добувають з наближеного значення числа, то результат потрібно заокруглити (за правилом 4) до трьох значущих цифр: .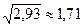

Застосування правил підрахунку цифр при обчисленнях на мікрокалькуляторах нічим не відрізняється від звичайних обчислень: спочатку машина обчислює результат, а потім його заокруглюють у відповідності з точністю вихідних даних за правилом підрахунку цифр.

Розглянемо приклади обчислення на мікрокалькуляторі із застосуванням правил 1 і 2.

Приклад 1.

Обчисліть суму: S=25,375+5,68-12,45+23,6473.

З допомогою мікрокалькулятора отримуємо результат: S=42,2523, який заокруглюємо до сотих (за правилом 1): S 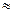45,25.

Приклад 2.

Обчисліть .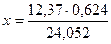

На мікрокалькуляторі ці дії виконуються без записування проміжного результату: х=0,3209246.

Так, як найменша кількість значущих цифр в компонентах три, то за правилом 2: х 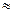0,321.

Як вже відмічалось, на мікрокалькуляторах деяких типів можна обчислювати значення функцій, що вивчаються в школі на уроках математика і застосовуються на уроках фізики. Для правильного заокруглення знайдених значень функцій можна користуватись правилами підрахунку цифр, розглянутими в параграфі 1.7. Наведемо приклади.

Приклад 3.

Обчислити . Маємо: (за правилом 8).

Приклад 4.

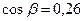. Знайдіть α.

На мікрокалькуляторі отримаємо: α=74,92994⁰. За правилом 9 результат потрібно заокруглити до градуса: α 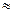75⁰.

Навчитись працювати з мікрокалькулятором неважко. Більшість учнів та студентів мають мікрокалькулятори і перестали витрачати багато часу на обчислювальну роботу при розв’язуванні задач і виконанні лабораторних робіт.

Довірчі імовірності для довірчого інтервалу вираженого у частинах середньої квадратичної похибки 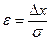. Функція Лапласа: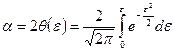

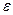
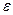
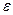
		1,2	0,77	2,6	0,990
0,05	0,04	1,3	0,80	2,7	0,993
0,1	0,08	1,4	0,84	2,8	0,995
0,15	0,12	1,5	0,87	2,9	0,996
0,2	0,16	1,6	0,89	3,0	0,997
0,3	0,24	1,7	0,91	3,1	0,9981
0,4	0,31	1,8	0,93	3,2	0,9986
0,5	0,38	1,9	0,94	3,3	0,9990
0,6	0,45	2,0	0,95	3,4	0,9993
0,7	0,51	2,1	0,964	3,5	0,9995
0,8	0,57	2,2	0,972	3,6	0,9997
0,9	0,63	2,3	0,978	3,7	0,9998
1,0	0,68	2,4	0,984	3,8	0,99986
1,1	0,73	2,5	0,988	3,9	0,99990
				4,0	0,99993

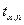Значення для різних значень довірчої імовірності та числа вимірювань

n ⇐ Предыдущая12131415161718192021Следующая ⇒ Не нашли, что искали? Воспользуйтесь поиском: