
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Таблицы истинности импликации 1 страница
| А | В | А ® В | А | В | А В | |
Отношение х Þ у не симметрично! Из х Þ у не следует, что у Þ х.
Обратим внимание на то, что отношение х Þ у ничего не утверждает про у, если посылка х задает ложное высказывание. Это значит, что если посылка ложна, то заключение может быть как ложным, так и истинным.
Из смысла отношения х Þ у («не может быть, чтобы х было верно, а у не верно») следует, что если у не верно, то и х не верно. Этот метод часто используется в математике при доказательстве теорем с помощью метода «от противного». Метод «от противного» состоит в получении противоречия с посылкой теоремы. Если требуется доказать, что из посылки х неизбежно следует заключение у (это и есть содержание доказываемой теоремы), то достаточно доказать, что из отрицания истинности заключения (т.е. из утверждения у) неизбежно следует отрицание истинности посылки (т.е. следует утверждение х). При этом утверждение х входит в противоречие с посылкой теоремы, утверждающей, что имеет место именно х. Это означает ошибочность утверждения у и тем самым (на основании закона исключения третьего) доказывает истинность утверждения у, составляющего заключение доказываемой теоремы.
Операция ® позволяет устанавливать формально, имеет ли место отношение логического следования между некоторой посылкой и некоторым заключением. Для этого следует посылку и заключение представить в форме высказываний и образовать импликативное выражение (высказывание). Если импликативное выражение всегда принимает значение истины, то данное заключение логически следует из данной посылки. В противном случае отношение логического следования не имеет места.
Допустимо применять только такие формы рассуждения, которые корректны всегда. Для оценки корректности (или наоборот – не корректности, то есть недопустимости) рассуждения надо выполнить следующие шаги.
1. Получить математическое описание рассуждения в виде формы сложного высказывания.
2. Исследовать на корректность полученную форму высказывания.
Для получения математического описания формы рассуждения необходимо от конкретных высказываний перейти к их символическому представлению и все высказывание записать с использованием логических связок.
Например, при попытке доказательства теоремы получено логическое выражение ((х ® у) Λ (х) ® у. Исследуем его на корректность.
Возьмем любое рассуждение вида х Þ у, в котором общее определение «у» выводится из частного определения «х».
х = «данное растение есть роза»;
у = «данное растение есть цветок».
Тогда
х = «данное растение не роза»;
у = «данное растение не цветок».
Подставим полученные высказывания в заданную форму рассуждения.
«((Если данное растение есть роза, то данное растение есть цветок) при этом данное растение не роза) следовательно, данное растение не цветок».
Абсурдность его очевидна, поскольку его второе предложение эквивалентно утверждению «цветов, отличных от розы, не бывает».
Исследуем полученное рассуждение ((х ® у) Λ (х) ® у формально:
1. Исползуя тождество избавимся от импликации (х ® у) = (х V у): ((х ® у) Λ (х) ® у = ((х V у) Λ(х) ® у.
2. Дистрибутивность Λ относительно V х Λ (у V z) = ху V хz:
((х V у) Λ(х) ® у = (хх V ух) ® у.
3. Закон идемпотентности х Λ х = х: (хх V ух) ® у = (х V ух) ® у.
4. Дистрибутивность Λ относительно V, правило вынесения за скобки (х V ух) ® у = х (1 V у) ® у.
5. Свойств констант х V 1 = 1: х (1 V у) ® у = х ® у.
В результате преобразований получено логическое выражение, которое не всегда является истинным. Полученный вывод означает некорректность формы рассуждения, по которой построено конкретное исследуемое рассуждение.
Истинностные значения, которые принимает сложное высказывание при различных сочетаниях значений истинности, составляющих его высказываний, удобно задавать с помощью таблиц истинности (ТИ) (табл. 1).
Равнозначность
Высказывание х «у истинно тогда и только тогда, когда истинностные значения х и у равны, и ложно в противоположном случае. Операция «называется эквивалентностью, тождественностью. Логическую операция «можно рассматривать как двустороннюю импликацию, т.е. имеют место одновременно две импликации х ® у и у ® х: (х «у)=(х ® у)(у ® х).
Равнозначность можно представить в виде
х «у = ху V х у = (х = у) = (х ¹ у).
Упражнение 6. Среди следующих высказываний укажите составные, выделите в них простые, обозначьте каждое из них буквой. Запишите с помощью логических операций каждое составное высказывание.
1. Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.
2. Если число оканчивается на 0, то оно делится на 10.
3. Если у меня будет свободное время и не будет дождя, то я не буду писать сочинения, а пойду на дискотеку.
4. Если человек с детства и юности своей не давал нервам властвовать над собой, то они не привыкнут раздражаться и будут ему послушны.
5. Числа, кратные 4, кратны 2.
Таблица 1
Таблицы истинности
| Дизъюнкция | Конъюнкция | ||||||||
| Отрицание | А | В | A V B | А | В | A Λ B | |||
| А | А | ||||||||
| Равнозначность | Импликация | ||||||||
| А | В | A «B | А | В | A ® B | ||||
1. Использование основных понятий
и законов алгебры логики
Самым сложным для учеников оказывается заучивание таблиц истинности. Кроме этого, некоторое неудобство может вызвать непривычная запись логических выражений, так как нет твердоустоявшихся обозначений. Не следует и сильно «мудрствовать», то есть воспринимать обыкновенные математические знаки «<» и «>» как неизвестные или забытые логические операции. Кроме этого, необходимо обратить внимание на различие смысловой нагрузки цифры «1»: когда она обозначает цифру, а когда истинность логического выражения. Если имеют место отношения между величинами, например, <, <, >, >, то подразумевается число.
Примерное время выполнения заданий ЕГЭ – 2 мин.
Задания с решениями
Задание 1. Демоверсия ЕГЭ 2006.
Укажите, для какого из указанных значений числа Х истинно высказывание (X > 4) V ((X > 1) ® (X > 4)):
| 1) 1; | 3) 3; |
| 2) 2; | 4) 4. |
Решение
Способ 1. Логические выражения в скобках обозначим именами. Пусть (X > 4) = А, (X >1) = В. Тогда запись исходного выражения примет вид А V (B ® A). Преобразуем это выражение, используя правила исчисления высказываний: А V (B ® A) = А V B V А = А V В. Подставим вместо имен исходные логические выражения. Нас интересует вариант, когда все выражение истинно, т.е. равно 1. В результате получим неравенство: (Х > 4) V (X < 1) = 1. Исходя из предложенных вариантов ответов можно сделать вывод, что выражение X > 1 будет ложным только в случае Х = 1.
Способ 2. Нас интересует вариант, когда все выражение истинно, т.е. равно 1.
В данном задании мы имеем дело с операциями импликации и логического сложения (дизъюнкции, ИЛИ).
Таблица истинности для операции дизъюнкция
| Дизъюнкция | ||
| А | В | А V В |
В операции Дизъюнкции для истинности выражения хотя бы одно из выражений А или В должно быть истинно.
Рассмотрим выражение А = (X > 4). Исходя из вариантов ответов можно сделать вывод, что у нас нет значения Х больше 4 и поэтому выражение А = 0, т.е. ложно.
В таком случае требуется, чтобы выражение В было истинным.
Исходное выражение принимает вид 0 V ((X > 1) ® 0) = 1.
Выражение B ® A принимает вид (X > 1) ® 0.
Таблица истинности для операции импликации
| импликация | ||
| А | В | B ® A |
Исходя из исходного выражения и условия что данное высказывание должно быть истинным, в таблице истинности для B ® A надо найти такую строку, в которой А = 0 и B ® A = 1.
Это первая строка. Поэтому необходимо чтобы высказывание В было равно 0. Все выражение можно привести к виду: «неверно, что (X > 1)». Исходя из вариантов ответов, можно сделать вывод, что выражение X > 1 будет ложным только в случае Х = 1.
Ответ: № 1.
Задание 2. Демоверсия ЕГЭ 2008.
Определите, для какого числа Х истинно высказывание
((X < 5) ® (X < 3)) Λ ((X < 2) ® (X < 1)):
| 1) 1; | 3) 3; |
| 2) 2; | 4) 4. |
Решение
Способ 1. Заданное сложное логическое высказывание состоит из двух частей, соединенных отношением конъюнкции (логического умножения). Логическое умножение истинно лишь тогда, когда оба сомножителя истинны.
Используя схемы аксиом Исчисления высказываний, преобразуем логические выражения:
(X < 5) ® (X < 3) = (X < 5) V (X < 3) = (Х > 5) V (Х < 3);
(X < 2) ® (X < 1) = (X < 2) V (X < 1) = (Х > 2) V (Х < 1).
Решим систему полученных неравенств графическим способом на числовой оси:

Из полученного рисунка можно сделать вывод, что заданное высказывание будет истинно при Х > 5 и Х < 1 и на промежутке 2 < Х < 3. Из предложенных вариантов ответов подходит только ответ под № 2.
Способ 2. Нас интересует вариант, когда все выражение истинно, т.е. равно 1.
Таблицы истинности
| Конъюнкция | Импликация | |||||
| А | В | А Λ В | А | В | А ® В | |
Логическое умножение истинно лишь тогда, когда оба сомножителя истинны.
Выражение (X < 5) ® (X < 3) должно быть истинным.
Выражение (X < 2) ® (X < 1)должно быть истинным.
Проверим все заданные варианты значения Х.
Пусть Х = 1
(X <5) ® (X <3) = 1, т.к. (1<5)=1 и (1<3)=1, в операции следования 1 ® 1 = 1;
(X <2) ® (X <1) = 0, т.к. (1<2)=1, но (1<1)=0, в операции следования 1 ® 0 = 0.
Следовательно, данный вариант ответа не подходит.
Пусть Х = 2
(X <5) ® (X <3) = 1, т.к. (2<5)=1 и (2<3)=1, в операции следования 1 ® 1 = 1;
(X <2) ® (X <1) = 0, т.к. (2<2)=0 и (2<1)=0, в операции следования 0 ® 0 = 1.
Решение найдено, но необходимо все же проверить и оставшиеся варианты.
Пусть Х = 3
(X <5) ® (X <3) = 1, т.к. (3<5)=1, но (3<3)=0, в операции следования 1 ® 0 = 0;
(X <2) ® (X <1) = 0, т.к. (3<2)=0 и (3<1)=0, в операции следования 0 ® 0 = 1.
Следовательно, данный вариант ответа не подходит.
Пусть Х = 4
(X <5) ® (X <3) = 1, т.к. (4<5)=1, но (4<3)=0, в операции следования 1 ® 0 = 0;
(X <2) ® (X <1) = 0, т.к. (4<2)=0, и (4<1)=0, в операции следования 0 ® 0 = 1.
Следовательно, данный вариант ответа не подходит.
Ответ: № 2
Задание 3
Укажите, для какого числа Х истинно высказывание
((X ≥ 5) V (X > 5)) ® (X < 2):
| 1) 3; | 3) 6; |
| 2) 2; | 4) 5. |
Решение
Способ 1. Воспользуемся схемами аксиом исчисления высказываний. Сначала избавимся от отрицаний:
(X ≥ 5) = (X < 5), (X > 5) =(X ≤ 5).
Затем необходимо выполнить операцию в скобках:
(X < 5) V (X ≤ 5) = (X ≤ 5).
Используя закон де Моргана избавимся от импликации:
(X ≤ 5) ® (X < 2) = (X > 5) V (X < 2)
Исходя из предложенных вариантов ответов решением данной задачи будет Х = 6.
Ответ: № 3.
Способ 2. Графическая интерпретация решения задачи:

Исходя из предложенных вариантов ответов решением данной задачи будет Х = 6.
Ответ: № 3.
Способ 3. Множество чисел, удовлетворяющих высказыванию (X > 5) больше, чем высказыванию (X ≥ 5), так как в нем учитывается вариант при X = 5. При логическом сложении данных выражений получаем то, объем которого больше, а именно (X > 5). Значит можно преобразовать исходное выражение в новое: (X > 5) ® (X < 2).
Из свойства импликации: А ® В = А V В, значит можно преобразовать выражение (X > 5) ® (X < 2) = (X > 5) V (X < 2). Перед выражением (X > 5) получили двойное отрицание. Используем закон снятия двойного отрицания (х) = х, и получаем результирующее выражение (X > 5) V (X < 2).
Исходя из предложенных вариантов ответов, решением данной задачи будет Х = 6.
Ответ: № 3.
Задание 4
Определите, для какого числа Х истинно высказывание: ((X > 3) ® (X > 4)):
| 1) 1; | 3) 3; |
| 2) 2; | 4) 4. |
Решение
Способ 1. Пусть А = X > 3, В = X > 4. Тогда исходное выражение можно записать в виде (А ® В). Используя тождество, получаем А ® В = А V В. Перед операцией импликации стоял знак операции отрицания. Значит, итоговое выражение получим в виде (А V В) = А Λ В. Перейдем к исходному значению А и В: (X > 3) Λ(X > 4). Преобразуем высказывание с отрицанием: (X > 4) = Х < 4. Получаем результирующее высказывание: (X > 3) Λ (Х < 4). Исходя из предложенных вариантов ответов Х = 4.
Способ 2. Поочередно подставляем значения Х в высказывания:
Пусть Х =1: ((1 > 3) ® (1 > 4)) = не(ложь ® ложь) = не(истина)=ложь;
Пусть Х =2: ((2 > 3) ® (2 > 4)) = не(ложь ® ложь) = не(истина)=ложь;
Пусть Х =3: ((3 > 3) ® (3 > 4)) = не(ложь ® ложь) = не(истина)=ложь;
Пусть Х =4: ((4 > 3) ® (4 > 4)) = не(истина ® ложь) = не(ложь)=истина.
Способ 3. Нас интересует вариант, когда все выражение истинно, т.е. равно 1. Поэтому выражение (X > 3) ® (X > 4) должно быть ложью. Из определения импликации следует, что высказывание (X > 3) должно быть истинно, а (X > 4) ложно. Этим условиям из целых чисел удовлетворяет только число 4.
Ответ: № 4.
Способ 4. Обозначим выражение (X > 3) ® (X > 4) = С. В таком случае исходный вопрос задачи будет формулироваться в виде: «для какого Х истинно С». Данную формулировку можно заменить на следующую: «для какого Х ложно С». Из определения импликации следует, что высказывание (X > 3) должно быть истинно, а (X > 4) ложно. Этим условиям из целых чисел удовлетворяет только число 4.
Ответ: № 4.
Задание 5
Определите, для какого имени истинно высказывание
(Первая буква имени гласная ® четвертая буква имени согласная):
| 1) ЕЛЕНА; | 3) ВАДИМ; |
| 2) БЭЛЛА; | 4) ЕВГЕНИЙ. |
Решение
Способ 1. Запишем условие буквенным выражением. Пусть гласные буквы будут обозначаться символом g, а согласные – символом s. После символа буквы поставим её порядковый номер. В таком случае выражение примет вид (g1 ® s4). Преобразуем данное выражение, избавимся от операции импликации, используя тождество (х ® у) = (х V у).
Исходное выражение примет вид (g1 ® s4) = (g1 V s4). Используем закон де Моргана: (х V у) = х Λ у. При этом получим: (g1 V s4) = g1 Λ s4. g1 = g1 по закону снятия двойного отрицания. Получаем выражение g1 Λ s4. По свойству исходных данных в данном задании s = g. Результирующее выражение будет иметь вид g1 Λ g4.
В предложенных вариантах ответов первая гласная буква присутствует в номерах 1 и 4. На четвертой позиции гласная буква стоит только в ответе под номером 4.
Ответ: № 4.
Способ 2. Необходимо, чтобы все выражение было истинно, т.е. равно 1. Поскольку перед скобками стоит знак отрицания, то для получения истинности всего выражения, выражение в скобках должно быть ложно.
Высказывания внутри скобок связанны импликацией. Из таблицы истинности импликации известно, что результат будет ложью только в том случае, если первое высказывание будет истинно, а второе ложно. Исходя их данных задания:
− высказывание «первая буква имени гласная» должно быть истинно;
− высказывание «четвертая буква имени согласная» должно быть ложно.
Первое высказывание будет истинно при рассмотрении имен ЕЛЕНА и ЕВГЕНИЙ. Второе высказывание будет ложно при рассмотрении имени ЕВГЕНИЙ.
Ответ: № 4.
Задание 6
Определите, для какого числа Х истинно высказывание
((X > 5) V ( X > 5)) ® (X < 2):
| 1) 1; | 3) 4; |
| 2) 2; | 4) 5. |
Решение
Способ 1. Высказывание (X > 5) V ( X > 5) = 1 будет истинным на всей числовой оси. На основании определения импликации правильный ответ будет там где X < 2 = 1.
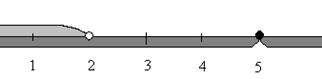
Ответ: № 1.
Способ 2. Нас интересует вариант, когда все выражение истинно, т.е. равно 1.
Если принять выражение X > 5 = а, то выражение (X > 5) будет равно а (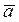 ). По закону исключения третьего a V
). По закону исключения третьего a V 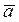 = 1.
= 1.
По таблице истинности импликации, если первое высказывание истинно, то для истинности всего выражения, необходимо чтобы второе высказывание тоже было истинным. Таким образом, выражение X < 2 должно быть истинным. В таком случае Х должен быть равен 1. Ответом является Х = 1.
Ответ: № 1.
Задание 7
Определите, для какого символьного выражения неверно
(первая буква гласная) ® (третья буква согласная):
| 1) abedc; | 3) babas; |
| 2) becde; | 4) abcab. |
Решение
Способ 1. Запишем условие буквенным выражением. Пусть гласные буквы будут обозначаться символом g, а согласные – символом s. После символа буквы поставим её порядковый номер. В таком случае выражение примет вид g1 ® s3. Преобразуем данное выражение, избавимся от операции импликации (х ® у) = (х V у).
Исходное выражение примет вид g1 ® s3 = g1 V s3.
По свойству исходных данных в данном задании s = g и s = g. Результирующее выражение будет иметь вид s1 V g3. Данное выражение будет истинным, если истинным будет хотя бы одно из составляющих его высказываний.
В предложенных вариантах ответов первая согласная буква присутствует в номерах 2 и 3. На третьей позиции гласная буква находится в ответе под номером 1. В ответе под номером 4 не выполняются оба условия.
Ответ: № 4.
Способ 2. Данное выражение представляет собою импликацию. Импликация является ложной тогда и только тогда, когда из истинной предпосылки (первого высказывания) следует ложный вывод (второе высказывание). В результате получаем: (первая буква гласная) = истинна; (третья буква согласная) = ложь, т. е. (третья буква согласная) = истина.
Ответ: № 4.
Задание 8
Определите, для какого числа Х истинно высказывание
(Х > 2) V (Х > 5) ® (Х < 3):
| 1) 5; | 3) 3; |
| 2) 2; | 4) 4. |
Решение
Для выполнения данного задания необходимо вспомнить приоритет выполнения связок (в порядке убывания приоритета): отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность.
Способ 1. Выражению (Х > 2) удовлетворяет больший объем чисел, чем выражению (Х > 5). Поскольку они соединены операцией логического сложения, то высказывание (Х > 2) поглощает высказывание (Х > 5).
Преобразуем исходное выражение: (Х > 2) ® (Х < 3).
Из предложенных вариантов ответов видно, что одновременно эти высказывания не могут быть истинными, равно как одновременно не могут быть и ложными. Рассмотрим варианты, когда истинно только одно из высказываний. Нас интересует вариант, когда все выражение истинно, т.е. равно 1. Этому условию может удовлетворять только вариант 0 ® 1 = 1, т.е. первое высказывание должно быть ложным, а второе высказывание – истинным. Если второе высказывание – истинно, то из предложенных вариантов ответов будет подходить только один ответ Х = 2. При этом высказывание (Х > 2) будет ложным.
Ответ: № 2.
Способ 2. Составим таблицу истинности данного логического высказывания для предложенных значений Х: (Х > 2) V (Х > 5) ® (Х < 3).
| Х | Х > 2 | Х > 5 | (Х > 2) V(Х > 5) | Х < 3 | (Х > 2) V(Х > 5) ® (Х < 3) |
| истина | ложь | истина | ложь | ложь | |
| истина | ложь | истина | ложь | ложь | |
| истина | ложь | истина | ложь | ложь | |
| ложь | ложь | ложь | истина | истина |
Не нашли, что искали? Воспользуйтесь поиском: