
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Определение ускорение свободного падения с помощью математического маятника.
Упражнение 1. Порядок обработки прямых измерений. Определение периода колебаний математического маятника.
1. Получите у преподавателя значения длины нити математического маятника  и числа измерений
и числа измерений  периода колебаний.
периода колебаний.
2. Проведите  измерений периода колебаний маятника, результаты этих измерений внесите в табл. 3.
измерений периода колебаний маятника, результаты этих измерений внесите в табл. 3.
Таблица 3
| Nизм | 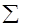
| |||||
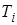 , с , с
| ||||||
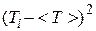
|
3. Просуммируйте все значения  и данную сумму занесите в соответствующую графу
и данную сумму занесите в соответствующую графу  . Используя значение этой суммы, по формуле (1) найдите среднее значение периода колебаний математического маятника
. Используя значение этой суммы, по формуле (1) найдите среднее значение периода колебаний математического маятника 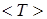 .
.
4. Зная 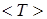 , заполните окончательно табл. 3, используя данные этой таблицы, найдите дисперсию среднего значение периода колебаний маятника по формуле (3).
, заполните окончательно табл. 3, используя данные этой таблицы, найдите дисперсию среднего значение периода колебаний маятника по формуле (3).
5. Найдите среднеквадратичное отклонение среднего значения по формуле 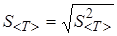
6. Задаваясь вероятностью  и зная число степеней свободы
и зная число степеней свободы  , определите по табл. 1 значение параметра Стьюдента
, определите по табл. 1 значение параметра Стьюдента  . Результат измерения периода колебаний запишите в виде
. Результат измерения периода колебаний запишите в виде  .
.
Упражнение 2. Обработка результатов косвенных измерений. Определение ускорения свободного падения.
1. Запишите в табл. 4 значения периода колебаний маятника. Эти данные возьмите из упражнения 1.
Таблица 4
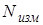
| 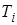 , с , с
| 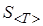
|  , м , м
| 
| 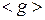 , м/с2 , м/с2
| 
|

|
2. Затем по формуле  вычислите среднее значение ускорения.
вычислите среднее значение ускорения.
3. Вычислите дисперсию ускорения свободного падения по формуле 
В качестве дисперсии длины маятника берется квадрат приборной погрешности. Дисперсия числа 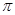 находится из Приложения 1.6.
находится из Приложения 1.6.
4. Найдите среднеквадратичное отклонение ускорения по формуле 
5. Результат измерения ускорения запишите в виде 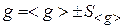 .
.
Упражнение 3. Порядок обработки совместных измерений. Определение ускорения свободного падения.
В этом упражнении необходимо определить ускорение свободного падения из совместных измерений длины математического маятника и его периода колебаний.
Период колебаний математического маятника вычисляется по формуле  . Для того чтобы воспользоваться методом обработки совместных измерений для зависимости
. Для того чтобы воспользоваться методом обработки совместных измерений для зависимости  введем следующие обозначения:
введем следующие обозначения:
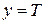 ;
; 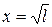 ;
;  .
.
Таким образом, зная экспериментальную зависимость  или
или  , можем вычислить коэффициент
, можем вычислить коэффициент 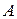 . Затем из соотношения
. Затем из соотношения 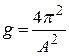 вычислим ускорение свободного падения.
вычислим ускорение свободного падения.
1. Получите у преподавателя значение пяти различных длин и определите период колебаний математического маятника.
2. Полученные данные запишите в табл. 5 (графы 2,3). В соответствии с вышеприведенными обозначениями заполните графы 4 и 5.
Таблица 5
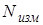
|  , м , м
|  , с , с
| 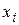
| 
| 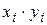
| 
| 
|
| … | |||||||
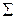
|
3. Проведите соответствующие вычисления и заполните графы 6,7 табл. 5. В графу 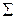 вносится сумма соответствующих колонок.
вносится сумма соответствующих колонок.
4. По формуле (15) вычислите значения параметра 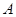 .
.
5. Проведите соответствующие расчеты и заполните графу 8.
6. Далее по формуле (16) вычислите дисперсии параметра А.
7. По формуле 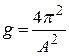 вычислите ускорение свободного падения.
вычислите ускорение свободного падения.
8. По формуле  вычислите среднеквадратичное отклонение ускорения свободного падения.
вычислите среднеквадратичное отклонение ускорения свободного падения.
9. Окончательный результат запишите в виде 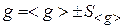 .
.
10. В координатах  постройте график зависимости
постройте график зависимости  , там же нанесите звездочками экспериментальные точки
, там же нанесите звездочками экспериментальные точки 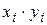 .
.
11. По формуле (20) найдите дисперсию адекватности. Дисперсию воспроизводимости найдите по формуле 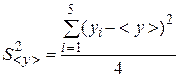 , где
, где 
 . Значения
. Значения  возьмите из первого упражнения. По этим данным найдите критерий Фишера. Сравнивая полученное значение критерия Фишера с табличным, сделайте окончательный вывод о соответствии зависимости
возьмите из первого упражнения. По этим данным найдите критерий Фишера. Сравнивая полученное значение критерия Фишера с табличным, сделайте окончательный вывод о соответствии зависимости  полученным экспериментальным данным.
полученным экспериментальным данным.
Приложение 1.1
Не нашли, что искали? Воспользуйтесь поиском: