
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Выявление области и оценка степени риска
В процессе экономической деятельности, как связанной, так и не связанной с инновациями, необходимо, прежде всего, выявить возможные области риска в каждом виде деятельности. Для этого возможно применение экспертных методов, позволяющих компенсировать недостаток информации о разрабатываемых или осуществляемых проектах, процессах, протекающих в экономике, явлениях хозяйственной жизни. Их использование базируется на информации, которой являются знания экспертов в данной области.
На этапе обнаружения риска, прежде всего, необходимо определить существование зон риска для проводимой работы, а при их наличии хотя бы качественно оценить важность этих рисков.
Алгоритм метода экспертной оценки экономических рисков включает в себя:
¨ разработку перечня возможных рисков по всем этапам и ключевым событиям реализуемого решения;
¨ определение опасности каждого риска для возможности реализации принимаемого управленческого решения и достижения поставленной цели;
¨ нахождение вероятности риска.
Опасность риска наиболее целесообразно представляется определять в процентах или долях единицы таким образом, чтобы сумма показателей по этапам и событиям реализуемого проекта или иного решения составляла 100% или единицу. Это позволит провести предварительный анализ структуры возможных опасностей риска, выделив наиболее важные, с данной точки зрения, этапы для дальнейшего контроля за их происхождением. Опасность можно также трактовать, как существенность последствий наступления риска на каком-нибудь этапе, связанная с возможностью исправления ошибки.
Допустима и балльная оценка опасности рисков. Однако ее применение не позволяет провести отмеченный структурный анализ.
Проведем примерный перечень рисков, возникающих при осуществлении инновационного проекта в научно-производственной сфере (см. табл. 1).
Таблица 1
Проектные риски в научно-производственной сфере
| № п/п | Наименование риска | Примечание |
| 1. | Содержание проекта | Возникает в связи с неверно поставленной задачей |
| 2. | Технологические решения | Возникает в связи с особенностями или ошибками в избранной технологии решения |
| 3. | Влияние государственных органов | Возникает, если проект является госзаказом, а также при изменениях в правовой базе и политической ситуации |
| 4. | Влияние органов экспертизы | Зависит от решения экспертного совета |
| 5. | Координация и согласован-ность разработки проекта | Возникает при наличии контрагентов по разработке проекта |
| 6. | Соответствие проектным стандартам | Возникает при отклонении проекта от ГОСТа, ОТУ и т.п. |
| 7. | Технические ошибки проекта | Связаны с ошибками технического решения (производства) |
| 8. | Утверждение результатов проектирования | Возникает на этапе утверждения проекта, изделия Госкомиссией или иным органом (структурой) |
| 9. | Квалификация и ресурсы проектирования | Более возможен при привлечении контрагентных организаций |
Приведенный перечень охватывает не все виды проектных рисков, а лишь наиболее характерные для любого проекта. Среди них есть как независимые один от другого, так и связанные. Например, технические ошибки нередко возникают из-за неудовлетворительной квалификации работников.
Рассмотрим, каковы наиболее рисковые зоны при разработке научно-технического проекта, возникающие, например, при разработке БИС-памяти (см. табл. 2)
Наиболее опасными зонами при разработке БИС-памяти являются, таким образом: технологические решения, технические ошибки проекта и само содержание проекта.
По имеющимся данным можно предположить наличие зависимости между показателями опасности, вероятности и важности риска. Чтобы убедиться в этом, ранжируем риски в порядке возрастания их опасности. Рядом запишем соответствующие им значения вероятности и важности.
Таблица 2
Определение рисковых зон при разработке БИС-памяти
| № | Наименование | Характеристика риска | ||
| п/п | риска | Опасность | Вероятность | Важность |
| 5 (3‘4) | ||||
| 1. | Содержание проекта: разработка БИС-памяти | 0,2 | ||
| 2. | Технологические решения: КМОП-технология | 0,5 | ||
| 3. | Влияние государственных органов: заказ МО | 0,3 | 2,4 | |
| 4. | Влияние органов экспертизы: решение экспертного совета | 0,4 | 3,2 | |
| 5. | Координация и согласованность разработки проекта: привлечение контрагентных организаций | 0,2 | ||
| 6. | Соответствие проектным стандартам: соответствие ОТУ | 0,1 | ||
| 7. | Технические ошибки проекта: точность изготовления фотошаблонов | 0,7 | 18,2 | |
| 8. | Утверждение результатов проектирова-ния: утверждение Госкомиссией | 0,2 | 0,6 | |
| 9. | Квалификация и ресурсы проектиров-щиков: квалификация и ресурсы контрагентов | 0,4 |
Подтвердим наличие отмеченной взаимосвязи расчетом скользящих трехуровневых средних. Для этого исчислим простую среднюю арифметическую
показателя вероятности риска, суммируя ее величины по первым трем его видам и деля полученную сумму на три. Последовательно отбрасывая показатель первого уровня и добавляя при этом показатель последующего уровня, получим средние значения вероятности для всех видов групп риска. Аналогично определены трехуровневые средние важности риска. Результаты расчетов (см. гр. 6, 7 табл. 3.) полностью подтверждают сделанные ранее предположения.
По данным таблицы 3 можно выделить по степени важности три группы риска:
I – риск, возникающий при научно-техническом решении задачи – позиции 1 и 2.
II – риск, связанный с выдачей задания и не зависящий от исполнителей – позиции 3 ё 5.
III – риск, связанный преимущественно с организацией выполнения работы – позиции 6ё9.
Таблица 3
Зависимость между опасностью, вероятностью и важностью риска
| № | Наименование риска | Опас-ность | Вероят-ность | Важ-ность | Трехуровневые средние | |
| п/п | Вероят-ность | Важ-ность | ||||
| 1. | Технологические решения: КМОП-технология | 0,5 | - | - | ||
| 2. | Технические ошибки проекта: точность изготовления фотошаблонов | 0,7 | 18,2 | 0,5 | 12,1 | |
| 3. | Содержание проекта: разработка БИС-памяти | 0,2 | 0,4 | 7,9 | ||
| 4. | Влияние государственных органов: заказ МО | 0,3 | 2,4 | 0,3 | 2,9 | |
| 5. | Влияние органов экспертизы: решение экспертного совета | 0,4 | 3,2 | 0,3 | 2,2 | |
| 6. | Координация и согласованность разработки проекта: привлечение контрагентных организаций | 0,2 | 0,3 | 2,1 | ||
| 7. | Квалификация и ресурсы проектиров-щиков: квалификация и ресурсы контрагентов | 0,4 | 0,3 | 1,2 | ||
| 8. | Утверждение результатов проектирова-ния: утверждение Госкомиссией | 0,2 | 0,6 | 0,2 | 0,9 | |
| 9. | Соответствие проектным стандартам: соответствие ОТУ | 0,1 | - | - |
Они характеризуются наличием:
I группа – наибольшей опасности, наивысшей вероятности и, следовательно, наибольшей важности риска;
II группа – умеренной опасности, средней вероятности и средней степени важности риска;
III группа – малой опасности, низкой вероятности и незначительной важности риска.
Подтвердим сказанное данными табл. 4, в которой приведем общие и средние групповые показатели опасности, вероятности и важности ключевых моментов разработки БИС-технологии.
Значительное превышение средних показателей I-ой группы над общими средними подтверждает правильность сделанного вывода.
Абсолютная величина экономических рисков, характеризующая принятие любого решения состоит из двух слагаемых:
Таблица 4
Средние показатели опасности, вероятности и важности ключевых моментов разработки БИС-технологии
| Средние характеристики | Опасность, % | Вероятность, доли ед. | Важность1), % |
| Общая средняя по всему проекту | 11,1 | 0,3 | 5,0 |
| Средняя I-ой группы | 28,0 | 0,6 | 16,6 |
| Средняя II-ой группы | 10,3 | 0,3 | 2,9 |
| Средняя III-ей группы | 3,3 | 0,2 | 0,9 |
1) Рассчитана как средняя из частных показателей по данным табл. 3.
¨ расходов, необходимых для осуществления данного решения;
¨ возможного ущерба, нанесенного этим решением.
Риск характеризуется также и относительными показателями. Один из них – степень риска. Он показывает, какова вероятность наступления случая потерь. Чем больше неопределенность ситуации при принятии решения, тем выше риск. Неопределенность хозяйственных ситуаций во многом обуславливается фактором случайности. Однако при большом числе наблюдений действие случайных факторов подчиняется определенным закономерностям. Числовыми характеристиками случайных событий являются вероятности этих событий.
В процессе наблюдений случайные события повторяются с определенной частотой, которая представляет собой отношение числа появления какого-либо события к общему числу наблюдений. Как правило, при большом числе наблюдений частота обладает статистической устойчивостью, т.е. ее значения мало изменяются. Таким образом, они как бы группируются около некоторого числа.
Объективное свойство случайного события, выражающееся через эту устойчивость, заключается в определенной степени его возможности. А мерой объективной возможности случайного события служит его вероятность. Вероятность изменяется в пределах от 0 до 1,0. Приближение вероятности какого-либо события к нулю свидетельствует о невозможности его наступления, и наоборот, – если вероятность равна единице, событие считается достоверным. Знание вероятности случайного события позволяет снизить уровень неопределенности и риска.
Следовательно, можно сделать вывод, что риск имеет количественную оценку, выраженную показателем вероятности наступления потери, рассчитанную методами и с помощью показателей математической статистики на базе статистических данных с достаточно высокой степенью точности.
Для определения величины риска необходимо знать абсолютные размеры последствий какого-либо решения, процесса, события, а также вероятность наступления этих последствий. Далее необходимо выбрать самое предпочтительное событие. При этом исходят из большей величины математического ожидания этого события.
Математическое ожидание какого-либо события равно произведению абсолютной величины этого события на вероятность его наступления. Математическое ожидание дискретной случайной величины равно сумме произведений возможных значений этой величины на их вероятности:
Е (х) =  хiрi = х1р1 + х2р2 +… +хnрn, (10.1)
хiрi = х1р1 + х2р2 +… +хnрn, (10.1)
Где Е – символ математического ожидания;
Е (х) – математическое ожидание случайной величины (события) х, очень часто называемое центром распределения, или центром рассеяния, а для нашего предмета исследования величина возможного риска;
хi – величина возможного ущерба в абсолютном выражении i-го варианта решения;
рi – вероятность того, что ущерб произойдет при i-ом варианте решения.
С помощью расчета величины риска (математического ожидания) можно выбирать решение как минимум из двух вариантов. Лучшим следует считать то, при котором рассчитанная величина риска наименьшая.
Заметим, что математическое ожидание случайной величины равно средней ее значений, взвешенной по вероятностям или:
Е (х) = ( ) (10.2)
) (10.2)
Данное уточнение в ряде случае позволяет существенно упростить расчеты. Рассмотрим следующий пример:
Имеются два опытных образца продукции, готовых к производству. Расчетным путем определено, что при вложении средств в производство изделия А будет получено 20 тыс. ден. ед. прибыли с вероятностью 0,6 а в изделия Б – будет получено 25 тыс. ден. ед. прибыли с вероятностью 0,4.
Ожидаемое получение прибыли от вложенных средств (математическое ожидание) составит:
по изделию А – 20 ґ 0,6 = 12 (тыс. ден. ед.);
по изделию Б – 25 ґ 0,4 = 10 (тыс. ден. ед.).
Следовательно, предпочтительно организовать производство изделия А, поскольку из двух имеющихся вариантов вложения средств математическое ожидание по данному проекту будет наибольшим.
Вероятность наступления какого-либо события может быть определена двумя методами – объективным и субъективным.
Объективный метод определения вероятности заключается в вычислении частоты, с которой происходит изучаемое событие. Например, если известно, что при вложении средств в производство изделия А прибыль в размере 20 тыс. ден. ед. будет получена в 120 случаях из 200, то вероятность ее получения составит 0,6 (120: 200).
Субъективный метод определения вероятности базируется на использовании субъективных критериев, исходящих из определенных предположений. Такими предположениями могут являться: суждение специалиста-аналитика, заключение эксперта, опыт руководителя, мнение консультанта и т.д. При этом каждый субъект анализа может предположить и установить различное значение вероятности для одного и того же события, что необходимо учитывать при выборе окончательного варианта при принятии решения.
Характеристиками степени риска являются также:
¨ среднее ожидаемое значение;
¨ колеблемость возможного результата.
Показатель среднего ожидаемого значения рассчитывается как средневзвешенная из всех возможных результатов, а в качестве весов при его исчислении принимается вероятность каждого результата или, иначе говоря, вес соответствующего значения.
Среднее ожидаемое значение связано с неопределенностью ситуации, в которой принимается решение, а потому оно характеризует результат, ожидаемый в среднем. Рассмотрим следующий пример:
При использовании новых форм сбыта продукции предприятие при продаже 80 единиц получило прибыль в размере 25 тыс. ден. ед., при продаже 60 единиц – 30 тыс. ден. ед., а при продаже еще 60 единиц – 20 тыс. ден. ед. Всего было реализовано 200 единиц продукции.
Рассчитаем показатели вероятности для имеющихся случаев и получим:
р = 80: 200 = 0,4;
р = 60: 200 = 0,3;
р = 60: 200 = 0,3.
Тогда среднее ожидаемое значение составит:
Е (х) = 25 ґ 0,4 + 30 ґ 0,3 + 20 ґ 0,3 = 25 тыс. ден. ед.,
где р – вероятность наступления события;
Е (х) – среднее ожидаемое значение.
В то же время при продаже продукции в традиционной форме прибыль в размере 25 тыс. ден. ед. была получена в 60 случаях из 200, в размере 30 тыс. ден. ед.– в 75 случаях и в размере 20 тыс. ден. ед. – в 65 случаях.
При старом варианте среднее ожидаемое значение составит:
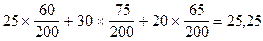 (тыс. ден. ед.).
(тыс. ден. ед.).
Сравнивая полученные результаты при старых и новых формах сбыта продукции, можно заметить, что при одинаковом колебании прибыли от 20 до 30 тыс. ден. ед., среднее ожидаемое ее значение при прежних формах сбыта выше, чем при новых на 250 ден. ед., что свидетельствует о нецелесообразности перехода на новые формы, несущего риск потери прибыли, равной этой величине.
Средняя величина является обобщенной характеристикой какого-либо процесса, явления, показателя. Оно не дает возможности сделать достаточно точный вывод о необходимости и целесообразности принятия определенного решения при наличии нескольких вариантов.
Этот недостаток устраняется с помощью показателей колеблемости. Они позволяют измерить отклонение значений изучаемого показателя от его средней, т.е. определить меру колеблемости возможного результата. Практически с этой целью можно применить один из показателей колеблемости.
Простейшим из них является размах вариации. Он исчисляется как разность между наибольшим и наименьшим значением показателя. Для двух вариантов решения он вполне приемлем, но при большом их числе колебания между значениями показателя не учитываются, и правильность выводов может быть поставлена под сомнение.
Наиболее часто для определения колеблемости признаков рассчитывают их дисперсию, среднее квадратическое отклонение, коэффициент вариации[38].
Покажем технику расчета дисперсии в табл. 5.
Таблица 5
Расчет дисперсии при выборе варианта сбыта продукции
| Форма сбыта и № события | Прибыль (х), тыс. ден. ед. | Число вариантов (f) | х ‘ f | 
| ( )2 )2
| ( )2‘ f )2‘ f
|
| 4 (2‘3) | 6 (52) | 7 (3‘6) | ||||
| Новая: | ||||||
| - | - | - | ||||
| Итого: | - | - | - | |||
| Старая: | ||||||
| 0,25 | 0,0625 | 3,75 | ||||
| 4,75 | 22,5625 | 1692,1875 | ||||
| 5,25 | 27,5625 | 1791,5626 | ||||
| Итого: | - | - | - | 3487,5 |
По полученным данным рассчитаем дисперсию прибыли при новом и старом вариантах сбыта продукции:
Новый способ: s2 =  .
.
Средняя прибыль для нового варианта: 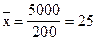 (тыс. ден. ед.)
(тыс. ден. ед.)
Средняя прибыль для старого варианта: 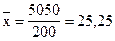 (тыс. ден. ед.)
(тыс. ден. ед.)
Тогда среднее квадратическое отклонение при новом способе сбыта продукции составит:
(= 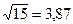 (тыс. ден. ед.),
(тыс. ден. ед.),
а коэффициент вариации:
(=. 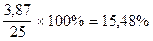
Соответственно для старого варианта сбыта:
s2 = 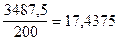 ;
;
(=  (тыс. ден. ед.);
(тыс. ден. ед.);
(= 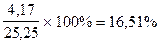 .
.
| Значение показателя вариации, %: | Область экономического риска: |
| 1. 0 – 5 | безрисковая область |
| 2. 5 – 10 | область минимального риска |
| 3. 10 – 30 | область повышенного риска |
| 4. 30 – 60 | область критического риска |
| 5. свыше 60 | область недопустимого риска |
Безрисковая область характеризуется отсутствием каких-либо потерь при осуществлении экономических проектов, хозяйственных операций и т.д. и получением расчетной прибыли.
Область минимального риска характеризуется уровнем потерь, не превышающим расходов на осуществление данного проекта или хозяйственной операции. При этом прибыль предприятия уменьшается на сумму данных затрат.
Область повышенного риска характеризуется потерей чистой прибыли, но получением валовой прибыли, позволяющей покрыть все ее затраты и первоочередные платежи (в бюджет, за кредит и т.п.).
В границах области критического риска возможны потери, превышающие размер чистой прибыли, но не превышающие размер валовой прибыли. Данный риск крайне нежелателен, так как подвергает предприятие опасности перехода в область недопустимого риска и не позволяет ему развиваться.
Область недопустимого риска характеризуется потерей не только чистой, но и части валовой прибыли, что не позволяет предприятию покрыть расходы или сделать первоочередные выплаты. Это делает его задолжником перед бюджетом и кредиторами. Просроченная задолженность по ссудам может составить 100 %, возможны потери в размере собственных средств, что ведет к банкротству предприятия.
Представим области экономического риска графически (см. рис. 2):
| Убытки | Прибыли | |||
| Свыше 60 | 30 – 60 | 10 – 30 | 5 – 10 | 0 – 5 |
| Область недопустимого риска | Область критического риска | Область повышенного риска | Область минимального риска | Область безрисковая |
Рис. 2. Области экономического риска.
Сравнивая полученные результаты можно придти к выводу, что, несмотря на более высокое значение ожидаемого среднего при старых формах сбыта продукции, колеблемость показателя прибыли при новом варианте сбыта ниже, чем при старом. Но, учитывая, что оба показателя вариации находятся вне области риска предприятию можно рекомендовать использовать новые формы реализации продукции для привлечения новых покупателей в целях завоевания рынка.
Таким образом, можно сделать заключение, что для идентификации риска необходимо и целесообразно использовать не какой-либо один метод, а весь арсенал имеющихся методов, с помощью которых следует строить систему оценочных показателей экономического риска и его областей применительно к сфере деятельности конкретного предприятия.
Не нашли, что искали? Воспользуйтесь поиском: