Пример выполнения домашней контрольной работы

Домашняя контрольная работа №1

Задача 1

	Определить усилия в стержнях кронштейна от приложенной внешней силы (рисунок А.1). Задачу выполнить аналитическим и графическим способами. Трением пренебречь.   F = 60 кН, α = 40о, β = 80о, γ = 50о.   .
Рисунок А.1

Решение

1 Выбираем точку, равновесие которой будем рассматривать − точка В.

2 Освобождаем узел В от связей и заменяем их реакциями, предполагая, что стержни растянуты, т. е. усилия направлены от узла.

Аналитический способ решения

3 Выбираем расположение осей координат так, чтобы одна из осей прошла через неизвестное усилие (N₁) (рисунок 2).

Рисунок А.2

4 Составляем уравнения равновесия.

; ;

; ;

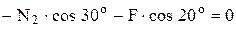(сжатие);

(растяжение).

Графический способ решения

3 Выбираем масштаб сил: 1 см = 10 кН.

4 Строим замкнутый силовой многоугольник (построение начинается с известной силы) (рисунок А.3).

Рисунок А.3

Измеряем полученные отрезки и умножаем их на масштаб.   N1 = 5,3 см ∙ 10 = 53 кН   Направление силы совпадает с первоначальным, значит, стержень 1 растягивается.   N2 = 6,5 см ∙ 10 = 65 кН   Направление силы не совпадает с первоначальным, значит, стержень 2 сжимается.

Ответ: стержень 1 − растянут (N₁ = 53,09 кН),

стержень 2 − сжат (N₂ = − 65,13 кН).

Задача 2

Определить опорные реакции консольной балки (рисунок А.4).

q = 5 кН/м, F = 15 кН, m = 20 кН∙м,

a₁ = 0,6 м, a₂ = 1,6 м, a₃ = 1,2 м, α = 60^о

Рисунок А.4

Решение

1 Выбираем направление опорных реакций.

2 Заменяем распределенную нагрузку сосредоточенной силой:

, (А.1)

где Q − величина сосредоточенной силы;

q − величина распределенной нагрузки;

− длина приложения распределенной нагрузки.

.

3 Составляем уравнения равновесия.

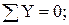
4 Для проверки составляем уравнение, не использованное при расчете:

.

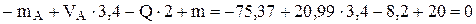Ответ: Н_А = 7,5 кН; V_A = 20,99 кН; m_A = 75,37 кН∙м.

Задача 3

Определить опорные реакции двухопорной балки (рисунок А.5).

q = 8 кН/м, F = 15 кН, m = 10 кН∙м,

a₁ = 0,5 м, a₂ = 0,8 м, a₃ = 1,4 м, а₄ = 0,6 м, α = 60^о

Рисунок А.5

Решение

1 Выбираем направление опорных реакций.

2 Заменяем распределенную нагрузку сосредоточенной по формуле (А.1):

.

3 Составляем уравнения равновесия:

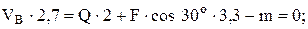
4 Для проверки составляем уравнение, не использованное при расчете:

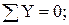
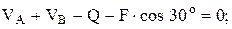
Ответ: H_A = 7,5 кН, V_A = 3,72 кН, V_B = 20,47 кН.

Задача 4

Определить координаты центра тяжести поперечного сечения геометрической формы (рисунок А.6). Построить в выбранном масштабе.

	а = 60 см; b = 80 см;   h1 = 30 см; h2 = 20 см; h3 = 40 см.
Рисунок А.6

Решение

1 Сложную фигуру разбиваем на сумму простых фигур: прямоугольник площадью А₁, прямоугольник площадью А₂, трапеция площадью А₃ (рисунок А.7).

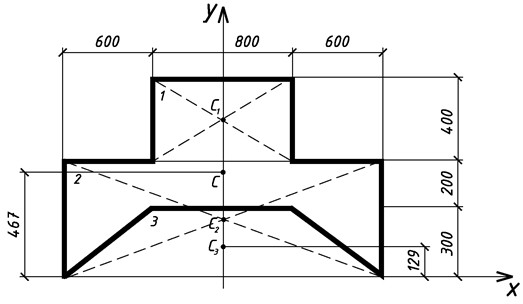
Рисунок А.7

2 Заданное поперечное сечение имеет вертикальную ось симметрии (ось У) и центр тяжести лежит на этой оси. Следовательно, относительно системы координат ХУ координата центра тяжести всего сечения х_с = 0, требуется определить координату у_с по формуле:

, (А.2)

где S_x − статический момент поперечного сечения;

А − площадь поперечного сечения;

A_i − площадь i-ой фигуры;

y_i − координата центра тяжести i-ой фигуры.

3 Находим площадь каждой фигуры и общую площадь поперечного сечения.

А₁ = b₁ ∙h₃ = 40∙80 = 3200 см²;

А₂ = (b + 2∙a)∙(h₁+h₂) = (80 + 2∙60)∙(30 + 20) = 10000 см²;

;

.

4 Находим координаты центров тяжести каждой простой фигуры относительно оси Х.

Для фигуры 1 (прямоугольник):

;

Для фигуры 2 (прямоугольник):

;

Для фигуры 3 (трапеция):

.

5 Вычисляем координату центра тяжести поперечного сечения:

.

Ответ: х_с = 0, у_с = 46,67 см.

Задача 5

Определить координаты центра тяжести сечения, составленного из стандартных профилей проката (рисунок А.8). Построить в выбранном масштабе.

Рисунок А.8

1 − Швеллер № 20;   2 − Двутавр № 16

Решение

1 Вычерчиваем заданное поперечное сечение (рисунок А.9). Размеры фигур берутся из таблиц сортамента (ГОСТ 8239-89, ГОСТ 8240-97).

Швеллер № 20:

h = 20 см, b = 7,6 см, d = 0,52 см, t = 0,9 см, z₀ = 2,07 см, А = 23,4 см².

Двутавр № 16:

h = 16 см, b = 8,1 см, d = 0,5 см, t = 0,78 см, А = 20,2 см².

Рисунок А.9

2 Заданное поперечное сечение имеет вертикальную ось симметрии (ось У) и центр тяжести лежит на этой оси. Следовательно, относительно системы координат ХУ координата центра тяжести всего сечения х_с = 0, требуется определить координату у_с по формуле (А.2).

3 Находим общую площадь поперечного сечения.

.

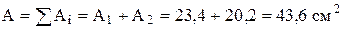4 Находим координаты центров тяжести фигур относительно оси Х.

Для фигуры 1 (швеллер):

;

Для фигуры 2 (двутавр):

.

5 Вычисляем координату центра тяжести поперечного сечения:

.

Ответ: х_с = 0, у_с = 11,46 см.

Домашняя контрольная работа №2

Задача 1

Для стального ступенчатого стержня (рисунок А.10) построить эпюры продольных сил N и нормальных напряжений σ и определить полное удлинение стержня.

Модуль продольной упругости материала Е = 2·10⁵ МПа = 2·10⁴ кН/см².

F₁ = 150 кН, F₂ = 70 кН, А = 20 см².

Решение   1 Используя метод сечений, определяем значения внутренних продольных сил N. Расчет ведем со стороны незакрепленного края стержня.   Сечение I − I N1 = 0;   Сечение II − II N2 + F1 = 0; N2 = − F1 = −150 кН (сжатие);   Сечение III − III N3 + F1 = 0; N3 = − F1 = −150 кН (сжатие);   Сечение IV − IV N4 + F1 + F2 = 0; N4 = − F1 − F2 = −150 − 70 = = − 220 кН (сжатие). По полученным значениям строим эпюру продольных сил N.   2 Определяем значения нормальных напряжений по формуле (3). , (3) где σ − величина нормального напряжения на участке, N − величина внутренней продольной силы, А − площадь сечения данного участка.

Рисунок А.10

,

,

,

.

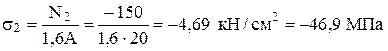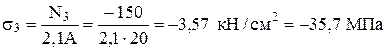По полученным значениям строим эпюру нормальных напряжений σ.

3 Определяем полное удлинение стержня по формуле (А.4):

, (А.4)

где - полное удлинение стержня,

- удлинение стержня на каждом участке.

Удлинение стержня на каждом участке находится по формуле (А.5):

, (А.5)

где N − величина продольной силы на участке,

− длина участка,

Е − модуль продольной упругости,

А − площадь поперечного сечения участка.

.

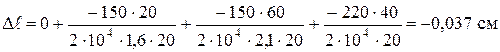Ответ: полное удлинение стержня = − 0,037 см.

Задача 2

Для двухопорной балки (рисунок А.11) построить эпюры поперечных сил Q и изгибающих моментов M и подобрать поперечное сечение в виде двутавра из условия прочности по нормальным напряжениям.

Расчетное сопротивление R = 210 МПа = 21 кН/см².

Коэффициент надежности по материалу γ_m = 0,9.

Решение

1 Определяем опорные реакции.

Проверка:

2 Строим эпюру поперечных сил Q.

Определяем значения поперечных сил в характерных сечениях.

Q_A = V_A = 17 кН,

Q_С = V_A = 17 кН,

Q_D =V_A – q∙4 = 17 – 8∙4 = −15 кН,

=V_A – q∙4 = −15 кН,

=V_A – q∙4 + V_B = 17 – 8∙4 + 20= 5 кН,

Q_Н =V_A – q∙4 + V_B = 5 кН.

Ординаты эпюры Q соединяем прямыми линиями.

3 Строим эпюру изгибающих моментов М.

М_А = 0 кН∙м,

М_С = V_A∙3 = 17∙3 = 51 кН∙м,

= V_A∙7 – q∙4∙2 = 17∙7 – 8∙4∙2 = 55 кН∙м,

= V_A∙7 – q∙4∙2 + m = 17∙7 – 8∙4∙2 + 10= 65 кН∙м,

М_В = V_A∙12 – q∙4∙7 + m = 17∙12 – 8∙4∙7 + 10= -10 кН∙м,

М_Н = V_A∙14 – q∙4∙9 + m + V_B∙2= 17∙14 – 8∙4∙9 + 10 + 20∙2= 0 кН∙м.

На участке АС эпюра М очерчена прямой линией. На участке СD приложена распределенная нагрузка, причем эпюра Q пересекает нулевую линию. Поэтому эпюра М будет очерчена параболой с экстремумом в точке пересечения (Q = 0). На участке DЕ эпюра М очерчена прямыми линиями.

Определим координату экстремума по формуле (А.6):

, (А.6)

где Q − величина поперечной силы в начале действия распределенной нагрузки;

q −.величина распределенной нагрузки.

.

Экстремальный изгибающий момент равен:

4 Определяем расчетный момент сопротивления сечения по формуле (А.7):

, (А.7)

где W_x − момент сопротивления,

М_max− максимальный (по абсолютному значению) изгибающий момент,

R − расчетное сопротивление материала,

− коэффициент надежности по материалу.

.

По таблице сортамента (ГОСТ 8239 − 89) выбираем двутавр № 27 с осевым моментом сопротивления W_x = 371 см³.

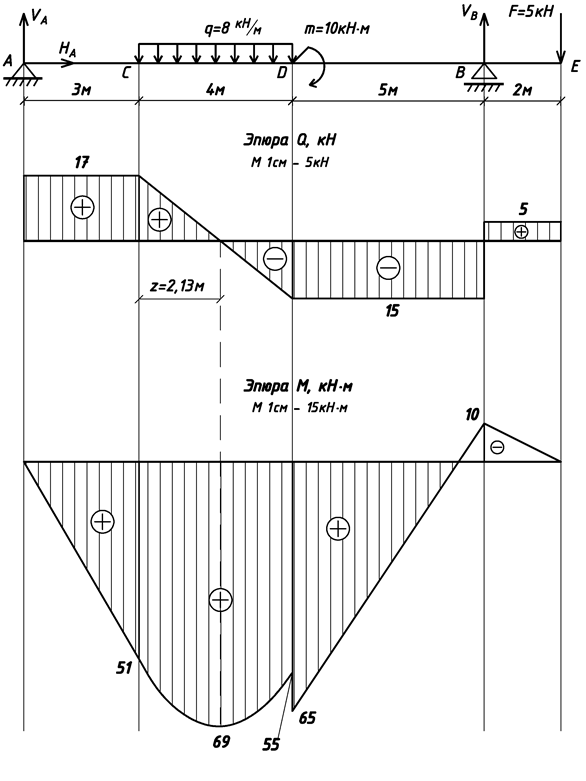
Рисунок А.11

Ответ: двутавр № 27.

Задача 3

Подобрать сечение равноустойчивой центрально-сжатой сквозной колонны из двух стальных швеллеров, соединенных между собой планками способом сварки (рисунок А.12).

Расчетное сопротивление материала R = 200 МПа, допускаемое напряжение [σ] = 150 МПа, коэффициент условия работы, = 1,0.

Рисунок А.12

Решение

1 Определяем необходимую площадь поперечного сечения из условия устойчивости:

, (8)

где А − площадь поперечного сечения;

F − величина приложенной силы;

φ − коэффициент продольного изгиба;

R − расчетное сопротивление;

− коэффициент условия работы.

Для первого приближения задаёмся произвольным коэффициентом продольного изгиба φ =0,75.

.

Площадь, приходящаяся на один швеллер равна 10 см²

По таблице сортамента (ГОСТ 8240-97) подбираем два швеллера № 10 площадью 10,9 см² и радиусом инерции относительно материальной оси i_y = 3,99 см².

Тогда площадь поперечного сечения колонны равна А=10,9∙2=21,8 см².

2 Определяем гибкость колонны относительно материальной оси по формуле (А.9):

, (А.9)

где − гибкость колонны относительно материальной оси У;

µ − коэффициент приведения длины;

− высота колонны;

i_у −радиус инерции относительно материальной оси.

.

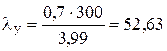3 Определяем коэффициент продольного изгиба методом линейной интерполяции (таблица Б.3).

λ = 50 φ = 0,869

λ = 60 φ = 0,827

для λ_у = 52,63 .

4 Производим проверку по условию устойчивости:

, (А.10)

.

Условие устойчивости не выполняется, следовательно, необходимо принять швеллеры большего размера.

5 Выбираем швеллер № 12 площадью 13,3 см² и радиусом инерции относительно материальной оси i_у=4,78 см². Тогда площадь поперечного сечения колонны равна А=13,3∙2=26,6 см².

Определяем гибкость колонны по формуле (А.9):

Определяем коэффициент продольного изгиба методом линейной интерполяции (таблица Б.3):

λ = 40 φ =0,906

λ = 50 φ =0,869

для λ_у = 43,93 .

Производим проверку по условию устойчивости (А.10):

Условие устойчивости выполняется.

Принимаем колонну с поперечным сечением, состоящую из двух швеллеров №12 с характеристиками: А=13,3 см², z_o=1,54 см, i_x1=4,78 см, I_x1=31,2 cм⁴.

6 Определяем требуемую гибкость колонны относительно свободной оси х по формуле:

, (А.11)

.

7 Требуемый радиус инерции для оси х равен:

8 Требуемый момент инерции поперечного сечения колонны:

. (А.12)

С другой стороны:

. (А.13)

Решаем совместно уравнения (А.12) и (А.13):

3554,65 = (31,2 + а² ∙13,3)∙2,

а = 11,5см.

9 Определяем расстояние , исходя из схемы поперечного сечения (рисунок А.12):

= 2∙(a + z_o) = 2∙(11,5 + 1,54) = 26,08 см.

Ответ: = 26,1 см.

Приложение Б

(справочное)

Не нашли, что искали? Воспользуйтесь поиском: