
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Множини. Деякі приклади числових множин
Множина – одне з важливіших понять математики, не означається через які-небудь інші елементарні поняття і вводиться аксіоматично. Описати термін множини можна як сукупність, об’єднання, набір деяких об’єктів довільної природи — елементів множини. Наприклад, множина книг в бібліотеці, множина книг в бібліотеці з даної галузі знань, множина студентів факультету, множина парних чисел, множина точок заданого відрізка і т.п. Як бачимо з прикладів множини можуть бути скінченними або нескінченними. Множини прийнято позначати великими буквами  а їх елементи – малими, наприклад,
а їх елементи – малими, наприклад,  .
.
Якщо елемент  належить множині
належить множині 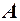 , то пишуть
, то пишуть  , якщо ж елемент
, якщо ж елемент  не належить множині
не належить множині 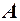 , то тоді пишуть
, то тоді пишуть  або
або 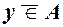 .
.
Множина, що не містить жодного елемента називається порожньою і позначається 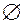 .
.
Розглянемо деякі означення.
Означення 1. Дві множини 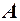 і
і  називаються рівними (позначають
називаються рівними (позначають 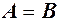 ), якщо вони складаються з однакових елементів.
), якщо вони складаються з однакових елементів.
Означення 2. Множина 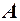 називається підмножною множини
називається підмножною множини  , якщо кожний елемент множини
, якщо кожний елемент множини 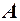 є елементом множини
є елементом множини  .
.
Це позначається так:  і читається “
і читається “ 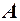 міститься в
міститься в  ” або “
” або “  включає
включає 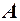 ”. Очевидно, що порожня множина включається в будь-яку множину
”. Очевидно, що порожня множина включається в будь-яку множину 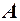 :
:  .
.
Наприклад, якщо множина 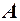 складається із елементів 1, 2, 3, 4, 5, 6, 7 (позначають
складається із елементів 1, 2, 3, 4, 5, 6, 7 (позначають  ), а
), а  , то
, то  .
.
Означення 3. Множина елементів  , які належать множині
, які належать множині 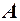 або множині
або множині  , або
, або 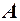 і
і  , називається об’єднанням цих множин і позначається
, називається об’єднанням цих множин і позначається  .
.
Означення 4. Множина елементів  , які належать обом множинам
, які належать обом множинам 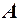 і
і  називається перерізом множин
називається перерізом множин 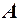 і
і  і позначається
і позначається
Якщо, наприклад, 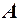 і
і  – це множини точок, що належать двом фігурам відповідно, то схематично на рис.1 зображені їх об’єднання у випадках а) і б). На рис.2 зображено переріз множин
– це множини точок, що належать двом фігурам відповідно, то схематично на рис.1 зображені їх об’єднання у випадках а) і б). На рис.2 зображено переріз множин 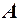 і
і  .
.

Рис.1.

Рис.2.
Означення 5. Різницею множин 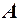 і
і  називається множина
називається множина  , що містить ті елементи
, що містить ті елементи 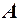 , які не є елементами множини
, які не є елементами множини  (див. рис.3).
(див. рис.3).

Рис. 3.
Задача. Нехай  . Знайти:
. Знайти:  .
.
Наведемо приклади відомих множин.
Множина натуральних чисел:  .
.
Множина цілих чисел: 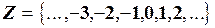 .
.
Множина раціональних чисел  – це числа вигляду
– це числа вигляду  , де
, де
 і
і  – цілі числа,
– цілі числа,  . Нагадаємо, що раціональні числа можуть виражатися десятковими дробами: скінченними або періодичними.
. Нагадаємо, що раціональні числа можуть виражатися десятковими дробами: скінченними або періодичними.
Числа, які виражаються нескінченними неперіодичними десятковими дробами називаються ірраціональними.
Об’єднання всіх раціональних і ірраціональних чисел утворюють множину  дійсних чисел.
дійсних чисел.
Має місце включення  .
.
Між множиною дійсних чисел та множиною точок числової вісі існує взаємно однозначна відповідність.
Не нашли, что искали? Воспользуйтесь поиском: