
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Абсолютна величина. Властивості абсолютних величин
Означення. Абсолютною величиною або модулем  (позначається
(позначається  ) називається невід’ємне значення, що збігається з
) називається невід’ємне значення, що збігається з  , якщо
, якщо  , і взяте із знаком мінус, якщо
, і взяте із знаком мінус, якщо  , тобто
, тобто
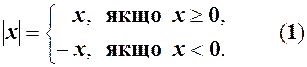
Наприклад, 
Мають місце такі властивості модулів:


Доведемо деякі із них. Спочатку переконаємось у вірності (2). Розглянемо два випадки:
а)  , тоді згідно (1)
, тоді згідно (1)  . В той же час
. В той же час  , тому за (1) маємо
, тому за (1) маємо  Отже
Отже  Тепер нехай
Тепер нехай  , тоді за (1) маємо
, тоді за (1) маємо  В той же час
В той же час 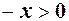 , тому
, тому  Отже
Отже 
Доведення нерівностей (3).
а) Якщо  , то в першому співвідношенні
, то в першому співвідношенні  , а в другому
, а в другому  .
.
б) Якщо ж  , то
, то  , а
, а  .
.
Аналогічно доводиться (4). Нехай
а)  , тоді згідно (1)
, тоді згідно (1)  , а згідно з (3) далі маємо
, а згідно з (3) далі маємо  .
.
б)  , тому знову таки згідно (1), (3) і (2) маємо
, тому знову таки згідно (1), (3) і (2) маємо

Властивість доведена.
Доведення нерівності (5).

Аналогічно

Оскільки  , то із отриманих співвідношень випливає нерівність (5).
, то із отриманих співвідношень випливає нерівність (5).
Нерівності (6) і (7) пропонуємо довести самостійно.
Звернемо увагу, що абсолютній величині можна дати геометричне пояснення: якщо задати на числовій осі  точку з абсцисою
точку з абсцисою  , то
, то  – це відстань цієї точки
– це відстань цієї точки  до точки
до точки  .
.
Означення та властивості модулів застосовуються при дослідженні функцій, побудові їх графіків, розв’язуванні рівнянь і нерівностей, які містять модулі.
Розглянемо деякі приклади.
Приклад 1. а) Побудувати графік функції  .
.
Розв’язання. Згідно (1)

Тому графіком функції  буде ламана, див. рис. 1.
буде ламана, див. рис. 1.

Рис. 1.
б) Розв’язати рівняння 
Розв’язання. Користуючись зображенням  за формулою (8) розв’язуємо спочатку рівняння
за формулою (8) розв’язуємо спочатку рівняння  на інтервалі
на інтервалі  . Оскільки
. Оскільки  , то
, то 
Якщо ж  то
то  , тому
, тому 
Якщо  , то маємо єдиний розв’язок
, то маємо єдиний розв’язок  .
.
Відповідь:  .
.
Зауважимо, що розв’язки  і
і  легко зрозуміти із
легко зрозуміти із
рис. 1. А якщо виходити з геометричного змісту абсолютної величини, то, очевидно, що на відстані  від точки
від точки  на осі
на осі  знаходяться дві точки
знаходяться дві точки  і
і  .
.
в) Розв’язати нерівність 
Розв’язання можна здійснити на кожному з інтервалів  і
і  , або простіше скористатись рис.1, з якого видно, що графік ламаної
, або простіше скористатись рис.1, з якого видно, що графік ламаної  знаходиться не вище прямої
знаходиться не вище прямої  для
для  , тобто
, тобто
 де
де  . (9)
. (9)
г) Розв’язати нерівність 
Розв’язок запишемо згідно з рис.1

Співвідношення (9) і (10) будуть використовуватись в подальшому.
Приклад 2. Записати без знака модуля вираз для функції  . Побудувати її графік.
. Побудувати її графік.
Розв’язання. Прирівняємо підмодульний вираз до нуля:  . Тепер розіб’ємо вісь на два інтервали:
. Тепер розіб’ємо вісь на два інтервали:  і
і 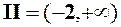 .
.


 І ІІ
І ІІ
–2 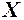
Якщо  , то
, то  , тому згідно з (1)
, тому згідно з (1)  .
.
Якщо ж  , то
, то 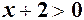 , тому
, тому  . Отже
. Отже
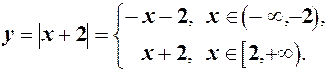
Будуємо окремо графіки:  для
для  і
і  для
для  . (див. рис.2)
. (див. рис.2)
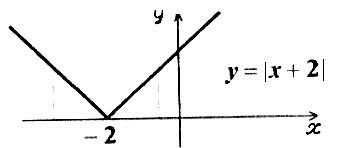
Рис.2
Ми бачимо, що графік функції  можна отримати паралельним перенесенням графіка
можна отримати паралельним перенесенням графіка  вліво вздовж осі
вліво вздовж осі  на дві одиниці.
на дві одиниці.
Очевидно, що в загальному графік функції  можна отримати паралельним перенесенням графіка
можна отримати паралельним перенесенням графіка  у напрямку осі
у напрямку осі  на
на  одиниць вправо, якщо
одиниць вправо, якщо  і вліво, якщо
і вліво, якщо  .
.
Як і в прикладі 1 після побудови графіка  можна легко знаходити розв’язок рівняння
можна легко знаходити розв’язок рівняння 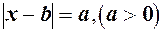 , а також нерівностей
, а також нерівностей  .
.
Приклади. Знайти розв’язки:
1)  . 2)
. 2) 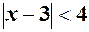 . 3)
. 3)  .
.
Відповіді: 1.  . 2.
. 2.  . 3.
. 3.  . Приклад 3. Побудувати графік функції
. Приклад 3. Побудувати графік функції  .
.
Розв’язання. Аналогічно попередньому прирівняємо до нуля підмодульний вираз: 
Розбиваємо вісь на три інтервали
 |
І. Якщо  , то
, то  тому
тому 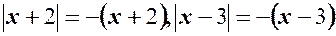 , і
, і 
ІІ. Якщо  , то
, то  і
і  , а
, а  і
і  , тому
, тому 
ІІІ. Якщо  , то
, то  тому
тому

Отже, для нашої функції маємо:

 |
її графік див. на рис.3.
Рис.3.
Завдання 1.
1. Побудувати графік функції  .
.
2. Розв’язати рівняння 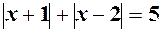 . Відповідь:
. Відповідь:  .
.
3. Розв’язати нерівність  . Відповідь:
. Відповідь: 
4. Побудувати графік функції  .
.
5. Записати вираз для функції  без модуля. Переконатись, що її графік відповідає зображеному на рис. 4.
без модуля. Переконатись, що її графік відповідає зображеному на рис. 4.
6. Записати вираз для функції  без модуля. Побудувати її
без модуля. Побудувати її
 |
графік.
Рис. 4.
Корисно звернути увагу на принцип побудови графіка функції  , якщо відомий графік
, якщо відомий графік  . Сподіваємось, що цей принцип зрозумілий із рис.5, де пунктиром зображено графік
. Сподіваємось, що цей принцип зрозумілий із рис.5, де пунктиром зображено графік  , а суцільною лінією
, а суцільною лінією  .
.
На інтервалах, де  обидва графіки збігаються, а там де
обидва графіки збігаються, а там де  , необхідно відобразити графік
, необхідно відобразити графік  симетрично
симетрично
 |
відносно вісі
 вверх, щоб отримати графік для
вверх, щоб отримати графік для  .
.
Рис.5
Завдання 2.
1. Користуючись результатами задач 5 і 6 попереднього завдання, а також сформульованим принципом, побудувати графіки
 і
і  .
.
Розв’язати рівняння та нерівності





Відповіді: 2. 1. 3. 0; 5 4. 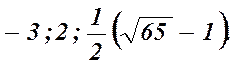 5. (0; 0,4).
5. (0; 0,4).
6. (-2; 3)
Не нашли, что искали? Воспользуйтесь поиском: