Швидкостей та прискорень. Контрольна №5

25. Задачі кінетостатичного дослідження механізмів. Принцип кінетостатики.

Задачею КАМ є визначення реакцій (тисків) у кінематичних парах механізму з урахуванням сил інерції, а також зрівноважувальної сили або зрівноважувального моменту, які прикладені до початкової ланки.

Принцип кінетостатики полягає в тому, що в число зовнішніх сил, що діють на ланки механізму, запроваджують сили інерції, які є фіктивними для самої ланки, але реальними для її зв'язків.

Принцип кінетостатики ґрунтується на відомому положенні Д'Аламбера, згідно з яким система сил, до якої уведені сили інерції, вважається рівноважною, і для неї придатні рівняння статики.

Отже, при включенні в число сил, що діють на ланку, сили інерції, ланка умовно вважається у стані спокою, тому можна застосовувати рівняння статики.

Цей принцип є методологічним.

26. Сили, що діють на ланки механізму.

Розглянемо блок-схему, наведену на рис. 5.1.

Рис. 5.1. Сили, що діють на ланки механізму

5.2.1. Рушійні сили – це сили, робота яких за цикл усталеного руху додатна.

.

(5.1)

Рушійні сили задаються у вигляді діаграм, наприклад (рис.5.2):

5.2.2. Сили опору – це сили, робота яких за цикл усталеного руху від'ємна.

5.2.2.1. Сили корисного опору – це сили, для подолання яких призначено механізм.

Сили корисного опору задаються у вигляді діаграм

5.2.2.2. Сили шкідливого опору – це сили, для подолання яких необхідно витратити роботу понад тої роботи, що йде на виконання технологічного процесу. Наприклад, сили тертя в кінематичних парах механізму.

5.2.3. Сили тяжіння

,

(5.2)

де - маса, кг; - прискорення вільного падіння, м/с².

Робота сил тяжіння за цикл усталеного руху дорівнює нулю.

5.2.4. Сили пружності

,

(5.3)

де - коефіцієнт жорсткості, Н/м; - переміщення, м.

Робота сил пружності за цикл усталеного руху дорівнює нулю.

27. Урахування сил інерції при плоскопаралельному русі ланки.

5.4.1. Плоско паралельний рух ланки

Згадаємо спочатку поняття маси і моменту інерції.

Маса – це міра інертності тіла при поступальному русі.

Момент інерції – це аналог маси при обертальному русі.

Зв'язок між масою і моментом інерції:

де - маса, кг; - радіус інерції, м.

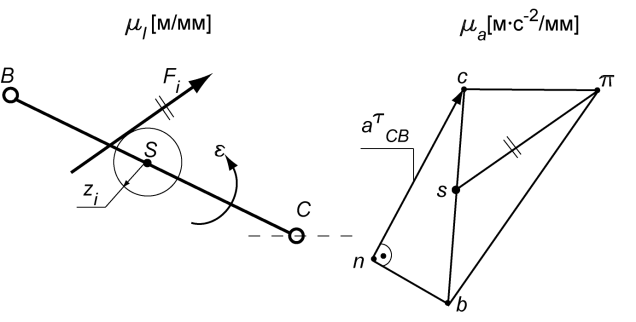
Розглянемо ланку ВС, яка здійснює плоскопаралельний рух (рис. 5.4,а) та її план прискорень (рис. 5.4,б).

Елементарна сила інерції для матеріальної точки визначається за формулою:

,

(5.5)

де - елементарна маса; - прискорення матеріальної точки.

Урахування сили інерції при плоскопаралельному русі ланки:

а. – ланка, що здійснює плоскопаралельний рух;

б. – план прискорень ланки

Виділяємо на ланці ВС (рис. 5.4,а) матеріальну точку D, тоді для неї:

.

Аналогічно для матеріальної точки К:

.

Але ланка – це система матеріальних точок, отже, для ланки маємо головний вектор сил інерції, Н:

,

(5.6)

де - маса ланки, кг; - прискорення центра мас ланки, м/с².

Ураховується також головний момент сил інерції, Нм:

,

(5.7)

де - момент інерції, кгм²; - кутове прискорення ланки, с^-2.

,

(5.8)

де - тангенціальне прискорення, м/с²; 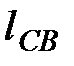- довжина ланки, м.

Для спрощення розрахунків головний вектор і головний момент сил інерції замінюються результуючою силою , плече якої h дорівнює (рис. 5.5):

або в масштабі: .	(5.9)
Рис. 5.5. Прикладання результуючої сили інерції

Із центра мас ланки S проводимо коло радіусом , результуюча сила прикладається по дотичній до цього кола, паралельно та протилежно (p s), і утворює момент проти e (рис. 5.5).

28. Урахування сил інерції при поступальному та обертальному рухах.

5.4.2. Поступальний рух ланки

При поступальному русі ланки враховується тільки головний вектор сил інерції , а головний момент сил інерції , т. щ. (рис. 5.6).

Рис. 5.6. Урахування сил інерції при поступальному русі	Рис. 5.7. Урахування сил інерції при обертальному русі навколо центральної осі

5.4.3. Обертальний рух ланки навколо центральної осі

При обертальному русі навколо центральної осі враховується тільки головний момент сил інерції , а головний вектор сил інерції ,т. щ. (рис. 5.7).

29.. Умови статичної визначуваності кінематичного ланцюга (КЛ)

5.5.1. Кінематичний ланцюг із нижчими парами

Нехай до ланки ВС із нижчими парами прикладені головний вектор і головний момент усіх сил, ураховуючи й сили інерції (рис. 5.9).

Невідомими є: - реакція в шарнірі В (невідома за величиною та напрямком); - реакція в поступальній парі (невідома за величиною та точкою прикладання).

Позначимо: – число рухомих ланок КЛ; – число рівнянь, які можна скласти; – число кінематичних пар (КП) 5-го класу; - число невідомих реакцій.

Перевіряємо умову статичної визначуваності для ланки:

замість умови маємо або .

Висновок:

У кінематичному ланцюгу з нижчими парами ланка з прикладеними до неї силами є статично невизначеною системою.

Отже, і механізм із нижчими парами є статично невизначеною системою.

Перевіряємо умову статичної визначуваності для групи Ассура:

(5.11)

або - умова статичної визначуваності групи Ассура.

Висновок: для визначення реакцій у кінематичних парах механізму його треба розділити на групи Ассура і для цих груп обчислювати невідомі реакції.

5.5.2. Кінематичний ланцюг із вищими парами

Нехай до ланки ВС із вищою парою С прикладені головний вектор і головний момент усіх сил, ураховуючи й сили інерції (рис. 5.10).

Невідомими є: - реакція в шарнірі В (невідома за величиною та напрямком); - реакція в поступальній парі (невідома за величиною), точка прикладання її відома.

Умова статичної визначуваності плоского КЛ із вищими парами:

або

,

(5.12)

отже, , 3=3.

Умова справедлива тільки для плоскої системи сил.

5.5.3. Умова статичної визначуваності просторового

кінематичного ланцюга (КЛ)

Для просторового КЛ справедлива умова:

або

.

(5.13)

32 Теорема М.Є. Жуковського

Якщо зрівноважену систему сил, що діють на ланки механізму, перенести в однойменні точки повернутого на 90⁰ плану швидкостей механізму, то сума моментів цих сил відносно полюса плану дорівнює нулю.

Доведемо цю теорему (див. рис. 5.13):

1. Нехай маємо механізм , на ланки якого діють сили ., що є рівнодіючими всіх сил і прикладені відповідно в т. (рис. 5.13,а).

2. На повернутий на 90⁰ план швидкостей у однойменні точки (знайдені за подібністю) переносимо сили (рис. 5.13,б).

3. Для доведення теореми скористаємося принципом можливих переміщень, відомий з курсу теоретичної механіки.

Сума елементарних робіт на можливих переміщеннях дорівнює нулю.

.

Треба довести, що .

4. Позначимо плечі сил , а також кути між векторами швидкостей та цими плечами.

5. Складаємо рівняння суми моментів усіх сил відносно полюса плану .

Скористаємося поняттям доведення від зворотного, тобто прирівнюємо суму моментів сил не нулю, а деякій величині А,

далі треба довести, що .

Рис. 5.13: До теореми Жуковського: а. – план механізму; б. – план швидкостей, повернутий на 900

6. Із плану швидкостей бачимо, що плечі сил , можна виразити таким чином:

.

(5.44)

7. Якщо помножити всі складові цього рівняння на масштаб , маємо швидкості точок :

.

або .

(5.45)

8. Розглянемо, що це за кути . Для цього переносимо вектори швидкостей на план механізму в точки , повертаючи їх попередньо на кут 90⁰ проти напряму повороту плану швидкостей (рис. 5.13,б). Як бачимо, це кути між векторами сил і векторами швидкостей (два останніх – між їх продовженнями).

9. Помножимо всі частини попереднього рівняння на (у лівій частині отримаємо елементарні переміщення точок ), а також урахуємо знаки “cos”:

(5.46)

Примітка: знаки “+” з'явилися за рахунок напрямів швидкостей.

10. Запишемо остаточно рівняння у формі “елементарних переміщень”:

11. У реальному механізмі всі елементарні переміщення є й можливими, отже: , але , отже, , що й треба було довести

33. Види тертя. Основні закони тертя ковзання незмащених тіл.

Експериментальні дослідження свідчать, що тертя являє собою складний комплекс механічних, фізичних та хімічних явищ, до того ж ті чи інші явища переважають залежно від умов, за яких відбувається процес тертя.

Розглянемо елементарні відомості з теорії тертя, необхідні для розв'язання найпростіших задач ТММ

Розрізняють два основних види тертя: сухе і рідинне.

Напівсухим тертям називається вид тертя, за якого найбільш виступаючі шорсткості не розділяються шаром мастила і безпосередньо контактують.

Різниця між напівсухим і напіврідинним тертям головним чином полягає в тому, який з основних видів тертя переважає.

Явища сухого і рідинного тертя за своєю природою зовсім різні, тому різними є і методи урахування сил тертя в механізмах. У фрикційних, пасових та інших передачах спостерігається сухе тертя; у змащених підшипниках, підп'ятниках тощо – рідинне тертя, яке інколи переходить в напівсухе чи навіть сухе (на час пуску машини). Внаслідок цього необхідно вивчати обидва види тертя.

Якщо виступаючи нерівності поверхонь А і В безпосередньо стикаються одне з одним, то такий вид тертя називається сухим.

Якщо між поверхнями А і В є проміжний шар мастила і поверхні А і В безпосередньо не стикаються, то такий вид тертя називається рідинним.

За відносним рухом розрізняють тертя ковзання та тертя кочення.

Тертя ковзання – це зовнішнє тертя за умови відносного ковзання тіл. що стикаються.

Тертя кочення (опір коченню) – це зовнішнє тертя за умови відносного кочення тіл, що стикаються

Розглянемо основні закономірності, що характеризують явище тертя ковзання незмащених тіл.

Нехай тіло, вага якого , знаходиться в спокої на похилій площині, яка має кут до горизонту (рис.6.3).

Розкладаємо силу на нормальну і тангенціальну складові: і ; - нормальна реакція похилої площини; - сила, яка виникає внаслідок тертя, спрямована паралельно площині.

Тертя спокою

Для рівноваги тіла (впливом перекидного моменту нехтуємо) необхідно, щоб виконувались такі умови: ;

34. Тертя в поступальній парі

Розглянемо, за яких умов повзун А почне рухатись по нерухомій напрямній В. Для цього перенесемо точку прикладання сили в точку О і розкладемо силу на складові та . Кут між напрямом сили і нормаллю позначимо . Тоді:

,	(6.10)
.	(6.11)

Від дії сили поверхні наближуються, а від дії сили повзун намагається зсунутись відносно напрямної.

Сила тертя за Кулоном - Амонтоном:

.

(6.12)

Повзун зсунеться з місця в той час, коли , де - сила тертя спокою.

Підставимо в рівняння для значення і :

.

(6.13)

Тоді:

.

(6.14)

Але , отже, повзун виходить зі стану спокою, коли , де - кут тертя спокою.

Із кулонівських положень відомо, що сила тертя руху менша за силу тертя спокою: , отже, і кут тертя руху менший за кут тертя спокою:

Висновок: Для урахування сил тертя в поступальній парі необхідно відхилити реакцію від напряму нормалі на кут тертя у бік, протилежний напряму швидкості повзуна відносно напрямної.

Якщо тіло знаходиться в спокої, то реакція відхилена від нормалі на кут, менший чи рівний куту тертя спокою

Повзун починає переміщуватись, коли .

Відкладаємо кут праворуч та ліворуч від нормалі (див. рис. 6.11). Тоді кут буде обмежувати деяку область рівноваги тіла.

Будь-яка сила, що прикладена в цій області під кутом , не може вивести повзун зі стану спокою.

Якщо надавати силі різні напрями в просторі, область рівноваги буде обмежена конусом тертя спокою (рис. 6.12), який може бути утворений обертанням кута тертя навколо нормалі до поверхонь, що дотикаються.

Аналогічно, якщо тіло рухається, то напрям сили повинен бути по твірній або ж ззовні конуса під кутом

35 Тертя в обертальній парі.

Тертя в обертальній парі (шипа по підшипнику,

п’яти по підп’ятнику).

Між валом 1 і підшипником 2 є радіальний зазор

,

Із попередніх положень про сили сухого тертя відомо, що сила повинна бути відхилена від нормалі на кут тертя , тоді сила тертя:

Момент , який прикладений до цапфи, зрівноважується моментом тертя :

де , а - радіус шипа.

Якщо з центра вала О описати коло радіуса , то повна реакція буде прикладена дотичне до цього кола

Коло радіуса називається колом тертя.

Коефіцієнт тертя визначається експериментально для різних умов роботи обертальних пар і змінюється в значних межах залежно від матеріалу, стану поверхні

. Тертя п'яти по підп'ятнику:на поверхні дотику п'яти і підп'ятника виникає сила тертя вертіння, яка відповідає закону Кулона - Амонтона

.

(6.51)

36. Тертя в гвинтовій кінематичній парі

Розглядаючи тертя в гвинтовій кінематичній парі, зазвичай, приймають ряд припущень.

По-перше, якщо закон розподілу тиску по гвинтовій різьбі невідомий, то умовно вважають, що сила тиску гайки на гвинт, чи, навпаки, гвинта на гайку прикладена по середній лінії різьби, розміщеній на відстані від осі гвинта.

По-друге, передбачається, що дія сил у гвинтовій парі може бути зведена до дії сил на повзун, який знаходиться на похилій площині..тертя у гвинтовій парі з трикутною різьбою більше, ніж у гвинтовій парі з прямокутною різьбою.

37. Рідинне тертя (тертя ковзання змащених тіл).

За умови рідинного тертя безпосереднє дотикання між двома поверхнями, які рухаються одна відносно однієї, відсутнє, тому що є проміжний шар рідини (мастила).

За умови відносного руху поверхонь спостерігається зсув окремих шарів рідини один відносно іншого. Отже, тертя в шарі рідини призводить до в'язкого зсуву.

Введемо поняття коефіцієнта рідинного тертя , який залежить від відносної швидкості руху шарів мастила, навантаження , а також коефіцієнта в'язкості ,

,

(6.54)

Ньютон дослідним шляхом довів, що за умови плоскопаралельного руху в'язкої рідини, величина сили , необхідної для переміщення одного шару рідини паралельно іншим, дорівнює:

де - площа поверхні ковзання; - градієнт швидкості

Основні вимоги для рідинного тертя:

Мастильна рідина, яка заповнює зазор між поверхнями, що труться, повинна утримуватись в зазорі. У шарі мастила за умови відносного ковзання змащуваних поверхонь повинен виникати і підтримуватись внутрішній тиск, який зпівноважить зовніщнє навантаження, притискаючи поверхні, що ковзають, одна до одної. Мастильна рідина повинна повністю розділяти поверхні, що ковзають. Шар рідини, який знаходиться між поверхнями, що ковзають, повинен мати товщину, не меншу мігімальної межі, яка визначається найбільш виступаючими частинами нерівностей поверхонь, що труться.

Тертя кочення

Якщо циліндр, навантажений силою , нерухомий (рис. 6.18, а), то в зоні дотику циліндра А і площини В виникає місцева деформація (її називають “пляма деформації”), і в точці С виникає опорна реакція (рівнодіюча напружень деформації), яка зрівноважує зовнішню силу .

Якщо циліндр перекочується, то “пляма деформації” зсовується в бік руху (рис. 6.18, б).

.

Рівнодіюча напружень зміщується праворуч від точки С на величину .

Величина називається плечем сили тертя кочення.

При коченні необхідно переборювати деякий момент , який називають моментом тертя кочення.

39. Тертя в механізмах з гнучкими ланками

Та гілка гнучкої ланки, яка, рухаючись, набігає на шків, називається гілкою, що набігає, а та, яка збігає зі шківа, називається гілкою, що збігає.

Дуга, на якій гнучка ланка дотикається до шківа, називається дугою обхвату, а відповідний їй центральний кут - кутом обхвату.

Нехай натяг гілки, що набігає, - , а гілки, що збігає, - .

натягнута зусиллями і гнучка ланка при може передавати веденому шківу обертовий момент , що дорівнює:

,

40. Задачі динамічного дослідження механізмів

Визначити закон руху ланок механізму за відомими: кінематичною схемою механізму; масовими характеристиками ланок; зовнішніми силами, що діють на ланки механізму

41. Метод зведення мас і сил при динамічному аналізі механізмів

Розглянемо багатоланковий механізм, на ланки якого діють сили

(рис. 7.5).

Відомі:

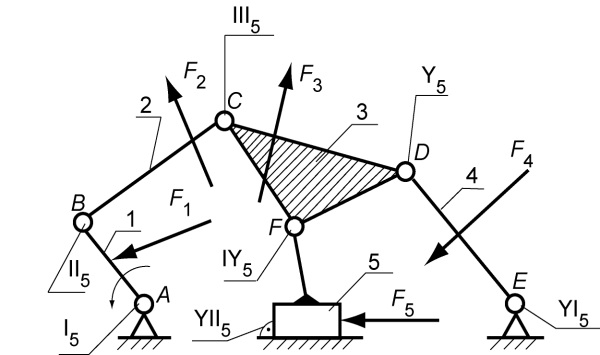
1. Кінематична схема механізму (КСМ).

2. Масові характеристики ланок.

3. Зовнішні сили, що діють на ланки механізму.

Треба визначити:

1. Лінійні швидкості та прискорення

2. Кутові швидкості та прискорення

1. Визначаємо степінь рухомості даного механізму за формулою Чебишева:

Потрібен 1 двигун.

2. Число рівнянь, які треба скласти для динамічного аналізу, як мінімум, дорівнює числу ланок і більше, якщо є ланки, що здійснюють плоскопаралельний рух (по 2 рівняння).

Отже, для полегшення дослідження механізм однократного степеня рухомості замінюється механізмом 1-го класу (одномасовою системою), динамічно еквівалентним вихідному механізму.

Еквівалентний механізм є складовою частиною заданого механізму. Його рухома ланка називається ланкою зведення.

На рис. 7.6 показані варіанти можливих замін.

Умови динамічної еквівалентності:

1. - кінетична енергія ланки зведення дорівнює сумі кінетичних енергій ланок механізму.

2. - миттєва потужність сил, які прикладені до ланки зведення, дорівнює сумі миттєвих потужностей сил,

що діють на ланки механізму.

Для виконання першої умови до ланки зведення додають додаткову масу, яка називається зведеною масою (або зведеним моментом інерції), володіючи якою ланка зведення має кінетичну енергію, яка дорівнює кінетичній енергії всіх ланок механізму.

Для виконання другої умови до ланки зведення прикладають зведену силу (зведений момент сили), миттєва потужність якої дорівнює миттєвій потужності всіх сил, що прикладені до ланок механізму.

Після заміни складають рівняння і визначають функції:

Ці рівняння визначають закон руху початкової ланки заданого механізму. Кінематичні функції решти ланок визначаються методами кінематики.

42. Зведена маса (зведений момент інерції).

Зведена маса (зведений момент інерції) – це розрахункова маса (момент інерції), володіючи якою ланка зведення має кінетичну енергію, яка дорівнює кінетичній енергії всіх ланок механізму.

Властивості зведеної маси (зведеного моменту інерції):

1. Є розрахунковою, а не фізичною величиною.

2. Для механізмів зі змінними передаточними функціями (ШВМ, кулачкові тощо) є змінною величиною.

3. Є функцією положення. Період змінювання дорівнює періоду усталеного руху.

За обчисленими значеннями зведеного моменту інерції будуються графіки в функції кута повороту ланки зведення .

Не нашли, что искали? Воспользуйтесь поиском: