
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Основний закон зачеплення
Нормаль профілів зубців завжди проходить через миттєвий центр обертання, який ділить міжосьову відстань на відрізки, обернено пропорційні кутовим швидкостям.
Профілі зубців, які задовольняють основному закону зачеплення, називаються спряженими.
Основна вимога до зубчастих механізмів:

|
 . .
|
Отже:
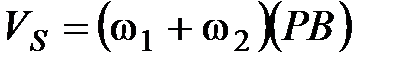 . .
|
Остаточно:
У полюсі зачеплення Р: 
Коефіцієнти відносного ковзання:

| (9.20) |
У полюсі зачеплення Р:  .
.
Висновки з основного закону зачеплення:
Профілями зубців можуть бути дві будь-які взаємообвідні лінії: пряма, парабола, гіпербола, евольвента тощо. Однак, профілі зубців мають відповідати ще й експлуатаційним умовам (технологічності, міцності, довговічності тощо), тому на практиці за профіль зубців приймають:
Ø евольвенту кола;
Ø циклоїдальні криві;
Ø дуги кола.
63. Евольвента кола та її властивості. Властивості евольвентного зачеплення.
Геометричне місце центрів кривизни будь-якої кривої називається еволютою, а її розгортка – евольвентою.
Евольвента кола – це крива, центри кривизни якої лежать на колі, що називається основним.
Евольвента описується точкою прямої, яка називається твірною, що котиться без ковзання по основному колу.
ВЛАСТИВОСТІ:
1. Дотична до основного кола є нормаллю до евольвенти в точці перетину з нею.
2. Точка дотику нормалі до евольвенти з основним колом є центром кривизни евольвенти.
3. Відстань по нормалі між рівновіддаленими евольвентами дорівнює довжині дуги основного кола між основами евольвент.
4. Із збільшенням радіуса основного кола  кривизна евольвенти зменшується, і при
кривизна евольвенти зменшується, і при  евольвента вироджується в пряму лінію.
евольвента вироджується в пряму лінію.
64. Кінематика евольвентного зачеплення.

|
наведена картина зовнішнього евольвентного зачеплення.
Міжосьова відстань:
 ,
,
де  ,
,  - радіуси початкових кіл.
- радіуси початкових кіл.
65. Методи виготовлення зубчастих коліс
Метод копіювання
При цьому методі зубчасті колеса нарізають інструментом, профіль якого точно збігається з профілем западин колеса, що нарізається, тобто профіль інструмента копіюється на колесі (див. рис. 9.9, а, б, в).
Інструментом може бути модульна (пальцьова або дискова) фреза. Обертаючись, фреза пересувається вздовж зубця. За кожний хід фрези нарізається одна западина. Після цього заготовка повертається на кутовий крок 
За допомогою цього методу можна нарізати прямозубі, косозубі та шевронні зубчасті колеса, для останніх заготовка в процесі нарізання повертається на відповідний кут. метод відливки (рис. 9.9, г ), коли зубчасте колесо є “відображенням” внутрішньої частини форми, що виконана у вигляді майбутнього зубчастого колеса. Відливанням виготовляють колеса великих розмірів, хоча позитивним фактором є те, що метод відливки – безвідхідний.
Метод обкатки (огинання)
При цьому методі в основу геометрії інструменту покладено так зване твірне колесо або рейку, бокові поверхні зубців яких мають різальні кромки.
При нарізанні зубців твірному колесу (інструменту) і колесу (заготовці), що нарізається, надаються відносні рухи, які б мали ці колеса, перебуваючи в зачепленні одне з одним. Зачеплення твірного колеса з оброблюваним колесом називається верстатним зачепленням.
На рис. 9.10, а показано нарізання зубців евольвентним твірним колесом (зуборізним довбачем). Довбач і заготовка здійснюють такі ж рухи, які б вони мали, знаходячись у зачепленні. Профіль зубця виходить як огинаюча всіх положень різальної кромки довбача.
Оскільки для будь-якого зубчастого колеса можна спроектувати спряжену з колесом зубчасту рейку, то замість інструмента-колеса може бути рейка, яка називається інструментальною рейкою (що випливає з однієї з властивостей евольвентного зачеплення (див п. 9.7).
У процесі нарізання рейка здійснює вздовж осі заготовки зворотно-поступальний рух (рис. 9.10,б). Заготовка має подвійний рух у горизонтальній площині: обертовий навколо своєї осі та поступальний вздовж рейки. Отже, заготовка здійснює рух колеса відносно рейки, і профілі зубців колеса одержують процесом обкатки. Весь процес здійснюється на спеціальних зубодовбальних верстатах.
На жаль, процес нарізування за допомогою рейки не є безперервним, що пояснюється обмеженою кількістю зубців самої рейки.
Після того, як заготовка перекотилася по всій довжині рейки, процес обкатки припинається, заготовку повертають у вихідне положення і продовжують обкатку. Це зменшує точність і продуктивність зубонарізування
66. Якісні показники зачеплення
Коефіцієнт перекриття 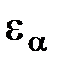
Цей коефіцієнт показує, скільки пар профілів зубців одночасно знаходиться в зачепленні. Він впливає на плавність і безшумність роботи
передачі. Визначається аналітичним і графічним шляхами
Коефіцієнти відносного ковзання 
Коефіцієнти відносного ковзання характеризують вплив сил тертя ковзання на зношування профілів зубців, тому що зубці перекочуються з ковзанням.
Коефіцієнт питомого тиску 
Коефіцієнт питомого тиску  використовується при розрахунках коліс на контактну міцність. Коефіцієнт
використовується при розрахунках коліс на контактну міцність. Коефіцієнт  розраховується в першу чергу в полюсі зачеплення
розраховується в першу чергу в полюсі зачеплення  аналітичним і графічним шляхами
аналітичним і графічним шляхами
67. Багатоланкові зубчасті механізми з нерухомими осями. Метод Смирнова-Куцбаха.
 , ,
|
1. Для побудови кінематичної схеми багатоланкового зубчастого механізму (рис. 9.13) визначаємо радіуси початкових кіл  , мм:
, мм:
де  - модуль зачеплення, мм (задається);
- модуль зачеплення, мм (задається);
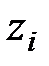 - число зубців коліс (задається).
- число зубців коліс (задається).
2. Накреслюємо в масштабі  кінематичну схему механізму (рис. 9.12, а). Позначаємо всі необхідні точки
кінематичну схему механізму (рис. 9.12, а). Позначаємо всі необхідні точки  .
.
 , ,
|
3. Визначаємо лінійну швидкість першого колеса, м/с:
де 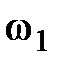 - кутова швидкість першого колеса, с-1;
- кутова швидкість першого колеса, с-1;
 , ,
|
де  - частота обертання першого вала, хв-1 (за завданням).
- частота обертання першого вала, хв-1 (за завданням).
 , ,
|
4. Приймаємо масштаб картини швидкостей  :
:
де 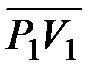 - відрізок, що зображує в масштабі
- відрізок, що зображує в масштабі  швидкість
швидкість 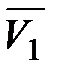 першого колеса. Для курсових проектів (робіт) рекомендується приймати в межах 60...100 мм.
першого колеса. Для курсових проектів (робіт) рекомендується приймати в межах 60...100 мм.

|
5. Відкладаємо відрізок 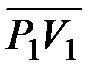 горизонтально від т.
горизонтально від т.  , наприклад, у правий бік (рис. 9.13, б), ставимо т.
, наприклад, у правий бік (рис. 9.13, б), ставимо т.  і з'єднуємо її з т.
і з'єднуємо її з т.  . Отримуємо трикутник швидкостей 1-го колеса -
. Отримуємо трикутник швидкостей 1-го колеса -  .
.
6. У полюсі зачеплення 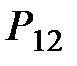 швидкості коліс 1 і 2 рівні:
швидкості коліс 1 і 2 рівні:  Отже, ставимо т.
Отже, ставимо т.  . Через т.
. Через т.  і т.
і т.  проводимо пряму до перетину з горизонтальною прямою, яка проведена з т.
проводимо пряму до перетину з горизонтальною прямою, яка проведена з т. 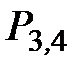 . Отримуємо т.
. Отримуємо т.  . Картини швидкостей 2-го і 3-го коліс – це відповідно
. Картини швидкостей 2-го і 3-го коліс – це відповідно  і
і  .
.
7. Через т.  і т.
і т.  проводимо пряму до перетину з горизонтальною прямою, яку проведено з т.
проводимо пряму до перетину з горизонтальною прямою, яку проведено з т.  .Отримуємо т.
.Отримуємо т.  . Картини швидкостей 4-го і 5-го коліс – це відповідно
. Картини швидкостей 4-го і 5-го коліс – це відповідно 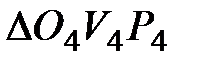 і
і  . З'єднуємо т.
. З'єднуємо т.  з центром
з центром  і отримуємо картину швидкостей 6-го колеса -
і отримуємо картину швидкостей 6-го колеса -  .
.
План кутових швидкостей (рис. 9.13, в) будуємо, продовживши вісь центрів  .
.
1. Проводимо горизонтальну вісь  .
.
2. Вибираємо полюсну відстань  .
.
3. Із полюса  проводимо промені до перетину з горизонтальною віссю
проводимо промені до перетину з горизонтальною віссю  , паралельні відповідним променям, а саме:
, паралельні відповідним променям, а саме: 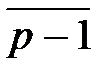 //
//  ,
,  //
//  і т.д.
і т.д.
4. Остаточно:
 ; ;
 ; ;

|
де  - масштаб частоти, хв-1/мм.
- масштаб частоти, хв-1/мм.
 . .
|
5. Масштаб кутової швидкості (для визначення кутових швидкостей), с-1/мм:
 . .
|
6. Отже, передаточне відношення, визначене графічним шляхом:
 , ,
|
де  - відрізки з плану кутових швидкостей
- відрізки з плану кутових швидкостей
68. Планетарні зубчасті передачі. Умови синтезу планетарних редукторів.
Планетарні зубчасті передачі – це передачі, в яких є зубчасті колеса, що обертаються як навколо власної осі, так і навколо центральної осі.
Такі колеса називаються сателітами.
Важіль, на якому розташовані осі сателітів, називається водилом.
Центральні зубчасті колеса називаються сонячними.
Якщо одне з центральних коліс нерухоме, а інше – рухоме, то механізм називається власно планетарним. Якщо всі колеса рухомі, то механізм називається диференціальним.
Редуктор – це зубчаста передача в корпусі, яка призначена для зниження кутової швидкості (частоти) та відповідно збільшення обертового моменту.
Задача синтезу планетарного редуктора полягає у визначенні кількості зубців зубчастих коліс за п'ятьма умовами
Умови:
1. Необхідне передаточне відношення:
 , ,
|
Загальна формула:
2. Умова співвісності:
Обидва центральних (сонячних) колеса та водило мають спільну геометричну вісь обертання, отже, для редуктора 2-го типа (рис. 9.14):
 або або
|
 , ,
|
3. Умова збирання:
При наявності одного сателіта великі відцентрові сили будуть згинати вісь водила – це недолік. Тому завжди беруть декілька сателітів, починаючи від  (
(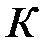 - кількість сателітів). Наприклад, у потужних танкових планетарних механізмах до 18 сателітів!
- кількість сателітів). Наприклад, у потужних танкових планетарних механізмах до 18 сателітів!
4. Умова сусідства:
Ураховуючи, що в планетарному механізмі декілька сателітів, треба так розташувати їх навколо першого сонячного колеса, щоб вони не чіпляли один одного зубцями (рис. 9.15).
На рис. 9.15:  - міжосьова відстань сателітів;
- міжосьова відстань сателітів;  - діаметр кола вершин сателітів;
- діаметр кола вершин сателітів; 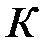 - кількість сателітів;
- кількість сателітів;  – зазор між вершинами зубців сателітів.
– зазор між вершинами зубців сателітів.
Загальна формула для всіх типів редукторів:
 , ,
|
де 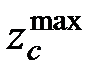 - число зубців більшого з двох сателітів (тобто
- число зубців більшого з двох сателітів (тобто  або
або 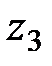 );
);
 – коефіцієнт висоти головки зубця;
– коефіцієнт висоти головки зубця;  - число сателітів
- число сателітів
5. Умова непідрізування (правильного зачеплення):
Ураховуючи, що всі колеса редуктора нульові, для запобігання підрізу зубця при  і
і 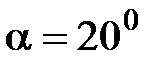 число зубців коліс редукторів має становити:
число зубців коліс редукторів має становити:
Для редуктора 1-го типа:
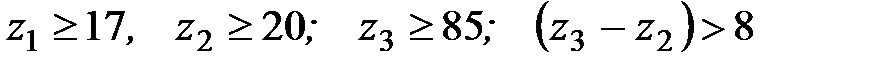 . .
|
Для редуктора 2-го типа:
 . .
|
Для редуктора 3-го типа:

|
Для редуктора 4-го типа:

|
Не нашли, что искали? Воспользуйтесь поиском: