
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Червячным редуктором 1 страница
| Наименование параметров и размерность | Обозначение | Величина |
| Мощность электродвигателя, кВт | Рэ. | |
| Требуемая мощность электродвигателя, кВт | Рэ тр.=Рвх. | 3,57 |
| Мощность на выходном валу, кВт | Рвых | 2,5 |
| КПД привода | η | 0,7…0,92 |
| Передаточное отношение (число) привода (редуктора) Частоты вращения валов, мин-1 (об/мин): вала электродвигателя (входного вала) | u nэ = n1 | |
| выходного вала редуктора | n2 = nвых. | |
| Угловые скорости вращения валов, рад/с: вала электродвигателя (входного вала) | ω1 | 78,5 |
| выходного вала редуктора | ω2 | 2,62 |
| Вращающие моменты на валах, Н·м: | ||
| на входном валу на выходном валу | Т1 Т2 | 45,44 954,2 |
| Диаметр вала электродвигателя, мм Ресурс работы, час | d'э t |
2 РАСЧЁТ ОДНОСТУПЕНЧАТОГО РЕДУКТОРА С
ЦИЛИНДРИЧЕСКОЙ ПРЯМОЗУБОЙ И КОСОЗУБОЙ ПЕРЕДАЧЕЙ
2.1 Расчетная схема. Исходные данные
На расчетную схему в условных обозначениях наносятся все известные параметры, а также параметры, подлежащие определению в этом разделе. Расчетная схема прямозубой передачи представлена на рисунке 2.1, косозубой передачи на рисунке 2.2.
Исходные данные для расчета прямозубой (косозубой) передачи берутся из условия задания и общего расчета привода:
вращающий момент на выходном валу Т2 = 114,6 Н·м;
передаточное число u = 5;
частота вращения и угловая скорость входного вала: n1 = 750 об/мин, ω1 = 78,5 рад/с,
частота вращения и угловая скорость выходного вала: n2 = 150 об/мин; ω2 = 15,7 рад/с;
ресурс работы t = Lh = 30000 часов.

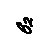
Рис. 2.1 Расчетная схема цилиндрической прямозубой передачи


Рис. 2.2 Расчетная схема цилиндрической косозубой передачи
2.2 Выбор материала и термической обработки колес
Материалы для изготовления зубчатых колес подбирают по таблице 16 [Р. 10]. В зависимости от условий эксплуатации, требований к габаритам передачи, технологии изготовления и с учетом экономических показателей применяют как среднеуглеродистые, так и высокоуглеродистые стали с различными вариантами термообработки (улучшение, закалка ТВЧ, цементация).
Чем выше твердость рабочей поверхности зубьев, тем выше допускаемые контактные напряжения [σ]Н и тем меньше размеры передачи, но сложнее технология изготовления колес и выше стоимость.
Для предотвращения заедания рабочих поверхностей твердость материала шестерни (меньшего колеса), как показывает практика, должна быть выше твердости колеса при одной и той же марке материала.
Так как в задании нет особых требований в отношении габаритов передачи, выбираем широко применяемые недорогие материалы (таблица 16 [Р. 10]): для колеса – сталь 40Х, термообработка – улучшение, твердость поверхности зубьев 235…262 НВ; для шестерни – сталь 40Х, термообработка – улучшение, твердость поверхности зубьев 269…302 НВ.
2.3 Допускаемые контактные напряжения
Допускаемые контактные напряжения определяют отдельно для колеса [σ]H2 и шестерни [σ]H1 по формуле
[σ]H = КHL[σ]HO,
где [σ]HO – допускаемые напряжения, соответствующие базовым числам циклов нагружений, [σ]HO = 1,8 НВср + 67 (таблица 17 [Р. 10]);
КHL – коэффициент долговечности при расчете по контактным напряжениям. При числе циклов перемены напряжений N больше базового NНО (N ≥ NНО) КHL = 1,0, при других значениях N рассчитывается по формуле
КHL = 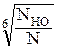 ≤ КHL max,
≤ КHL max,
где NHO - базовое число циклов нагружения;
N - действительное число циклов перемены напряжений;
KHLmax - максимальное значение коэффициента долговечности (при термообработке – улучшение KHLmax = 2,6, при термообработке закалка KHLmax = 1,8).
При расчете на контактную прочность базовые числа циклов нагружений определяют по формуле NНО = (НВ)3ср, в зависимости от средней твердости материала колес НВср = 0,5 (НВmin + НВmax). (2.1)
Действительные числа циклов перемены напряжений:
для колеса N2 = 60 · n2 · Lh; (2.2)
для шестерни N1 = N2 · u,
где Lh = t - ресурс работы передачи.
Допускаемые контактные напряжения определяют по формулам:
[σ ]Н1 = КHL1[σ]Н01; (2.3)
[σ ]Н2 = КHL2 [σ ] Н02.
В соответствии с изложенным определяется средняя твердость материала:
колеса НВср = 0,5 (235 + 262) = 248,5;
шестерни НВср = 0,5 (269 + 302) = 285,5.
Базовые числа циклов нагружений:
колеса NНО2 = 248,53 = 15,3 · 106;
шестерни NНО1 =285,53 = 23,3 · 106.
Действительные числа циклов перемены напряжений:
колеса N2 = 60 ·150·30000 = 270 ·106;
шестерни N1 = 270 ·106·5 = 1350 ·106.
Поскольку N2 = 270 ·106 > NНО2 = 15,3 ·106, то КHL2 = 1;
N1 = 1350 ·106 > NНО1 = 23,3·106, то КHL1 =1;
[σ ]Н02 = 1,8 ·248,5 + 67 = 514 Н/мм2;
[σ ]Н01 = 1,8 · 285,5 + 67 = 581 Н/мм2,
тогда допускаемые контактные напряжения будут иметь значения:
[σ ]Н2 = 514 Н/мм2, [σ ]Н1 = 581 Н/мм2.
Для дальнейших расчетов принимается меньшее из значений
[σ ]Н2 и [σ ]Н1, т.е. [σ ]Н = 514 Н/мм2.
2.4 Допускаемые изгибные напряжения
Допускаемые напряжения изгиба определяют отдельно для колеса [σ]F2 и шестерни [σ]F1 по формуле [σ]F = КFL [σ]F0,
где КFL – коэффициент долговечности при расчете на изгиб, КFL = 1,0 при N ≥ 4∙106; при других значениях N рассчитывается по формуле
КFL = 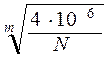 ≤ КFLmax,
≤ КFLmax,
где m - показатель степени, при термообработке - улучшение m = 6 и при термообработке – закалка m = 9;
KFLmax- максимальное значение коэффициента при термообработке - улучшение KFLmax = 2,08; при термообработке - закалка KFLmax = 1,63;
[σ]F0 – допускаемые предельные напряжения изгибной выносливости зубьев, соответствующие базовым числам циклов напряжений при расчете на изгиб NF0 = 4·106, выбираются по таблице 17 [Р. 10] в зависимости от средней твердости колес НВср. Для нашего случая [σ]F0 = 1,03 НВср.
Допускаемые изгибные напряжения для колеса и шестерни определяются по формулам:
[σ ]F2 = КFL2 [σ ]F02; (2.4)
[σ ]F1 = КFL1 [σ ]F01.
Так как действительные числа циклов перемены напряжений
N2 = 270 · 106 > 4·106, то КFL2 = 1;
N1 = 1350 · 106 > 4 · 106, то КFL1 = 1.
В этом случае: [σ]F02 = 1,03 · 248,5 = 256 Н/мм2;
[σ ]F01 = 1,03 · 285,5 = 294 Н/мм2,
и допускаемые изгибные напряжения будут иметь значения:
[σ]F2 = 256 Н/мм2, [σ]F1 = 294 Н/мм2.
2.5 Проектировочный и проверочный расчеты прямозубой передачи
2.5.1 Межосевое расстояние
Межосевое расстояние передачи определяется из условия контактной прочности зубьев
σН ≤ [σ]Н.
Межосевое расстояние
а ≥ К а (u +1)  , (2.5)
, (2.5)
где а – межосевое расстояние в мм;
К а – коэффициент межосевого расстояния (для прямозубых колес
К а = 49,5);
u – передаточное число;
ψ а – стандартное значение коэффициента ширины колес (при симметричном расположении колес относительно опор ψ а = 0,315);
Т2 – вращающий момент в Н·мм;
[σ]Н – допускаемое контактное напряжение в Н/мм2 (МПа);
КНβ – коэффициент концентрации нагрузки (при НВ≤350 КНβ = 1).
Таким образом:
а = 49,5 (5+1) 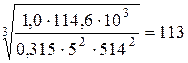 мм.
мм.
Вычисленное межосевое расстояние округляем в большую сторону до стандартного числа по таблице 1 [Р. 10] а = 120 мм.
2.5.2 Предварительные основные размеры прямозубого колеса
Делительный диаметр
d'2= 2 а ·u /(u + 1) = 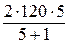 = 200 мм, (2.6)
= 200 мм, (2.6)
ширина колеса в 2 = Ψ а·а = 0,315 · 120 = 37,8 мм. (2.7)
Ширину колеса после вычисления округляем в ближайшую сторону до целого числа, т.е. в 2 = 38 мм.
2.5.3 Модуль передачи (зацепления)
Модуль зацепления является важнейшим параметром зубчатой передачи, он должен быть стандартным, одинаковым для колеса и шестерни, по нему нарезают зубья колес с помощью инструментальной рейки и рассчитывают геометрические параметры колес.
Предварительно модуль передачи определяют по формуле
m' ≥  , (2.8)
, (2.8)
где Кm = 6,8 - коэффициент модуля для прямозубых колес;
[σ]F - допускаемое изгибное напряжение, подставляют меньшее из [σ]F1 и [σ ]F2, т.е. [σ]F = [σ]F2 = 256 Н/мм2 (МПа).
Значение модуля передачи m в мм, полученное расчётом, округляют в большую сторону до стандартного (ГОСТ 9563-80) из ряда чисел (таблица 19 [Р. 10]).
При выборе модуля 1-й ряд следует предпочитать 2-му.
В результате расчета получим модуль передачи прямозубого зацепления
m' = 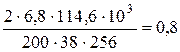 мм.
мм.
Принимаем стандартное значение m = 1 мм.
2.5.4 Числа зубьев прямозубых колес
Суммарное число зубьев для прямозубых колес
zΣ = 2 a / m2 = 2 ·120 /1,0 = 240. (2.9)
Число зубьев шестерни
z1 =  ; (2.10)
; (2.10)
где z1min = 17 – для прямозубых колес из условия не подрезания при нарезании.
Значение z1 округляют в ближайшую сторону до целого.
Число зубьев колеса
z2 = zΣ – z1. (2.11)
В результате вычислений получим:
z1 = 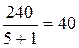 > 17;
> 17;
z2 = 240 – 40 = 200.
2.5.5 Фактическое передаточное число
Фактическое передаточное число
uф =  =
= 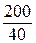 = 5.
= 5.
Допускаемое отклонение [∆u] ≤ 4%.
Отклонение от заданного передаточного числа
Δu =  %.
%.
Таким образом, для прямозубой передачи
Δu = 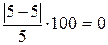 .
.
2.5.6 Размеры колеса прямозубой передачи
Делительные диаметры шестерни d1 и колеса d2 определяются с точностью расчета до первого знака после запятой:
d1 = z1· m; (2.12)
d2 = 2 a – d1.
Диаметры окружностей вершин d a и впадин зубьев d f:
шестерни d a 1 = d1 + 2m; d f 1 = d1 – 2,5m; (2.13)
колеса d a 2 = d2 + 2m; df 2 = d 2 – 2,5m.
Ширину шестерни в 1 (мм) принимают по соотношению в 1 /в 2,
где в 2 – ширина колеса.
При в 2 …….. до 30; св. 30 до 50; св.50 до 80; св.80 до 100
в 1 /в 2 …. 1,1; 1,08; 1,06; 1,05.
Полученное значение в 1 округляют до целого числа.
Определяем размеры колес:
шестерни d1 = 40 ·1,0 = 40 мм; колеса d2 = 2·120 – 40 = 200 мм.
Диаметры окружностей вершин зубьев:
шестерни d а 1 = 40 + 2 ·1,0 = 42 мм; колеса d а 2 = 200 + 2·1,0 = 202 мм.
Диаметры окружностей впадин зубьев:
шестерни d f 1 = 40 – 2,5·1,0 = 37,5 мм; колеса d f 2 = 200 – 2,5·1,0=197,5мм.
Ширина колеса в нашем случаи в 2 = 38 мм, тогда
в 1 = 38 · 1,08 = 41 мм.
Полученное значение в 1 округляют до целого числа.
Высота головки зуба h а = m = 1 мм.
Высота ножки зуба h f = 1,25· m = 1,25·1 = 1,25 мм.
Высота зуба h = h a + h f = 1 + 1,25 =2,25 мм.
Окружной шаг ρ = πm = 3,14 ·1 = 3,14 мм.
Толщина зуба s, равная ширине впадины «е», т.е.
s = e = 0,5ρ = 0,5·3,14 = 1,57 мм.
Радиальный зазор между зубьями с = 0,25m = 0,25 ∙ 1 = 0,25 мм.
2.5.7 Силы в зацеплении
В прямозубом зацеплении действуют окружная  и радиальная
и радиальная  силы. Осевая сила для прямозубой передачи равна нулю, так как β = 0.
силы. Осевая сила для прямозубой передачи равна нулю, так как β = 0.
Окружная сила
Ft = 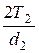 . (2.14)
. (2.14)
Радиальная сила
F r = Ft tgα, (2.15)
где α = 200 – стандартный угол зацепления.
Для стандартного угла tgα = tg200 = 0,364.
Осевая сила
F a = Ft tgβ. (2.16)
В результате расчетов прямозубого зацепления получим:
окружная сила Ft = 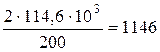 Н;
Н;
радиальная сила F r = 1146·0,364 = 417 Н;
осевая сила F a = 0.
2.5.8 Степень точности зацепления
Степень точности передачи определяют по таблице 20 ([Р. 10]) в зависимости от окружной скорости колеса
V = 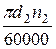 (м/с).
(м/с).
Окружная скорость прямозубого колеса
V = (3,14·200·150) /60000 = 1,57 м/с.
По окружной скорости определяем 9-ю пониженную степень точности зацепления.
2.5.9 Проверочный расчет зубьев колеса
Проверочный расчет производится по методикам, определенным ГОСТ 21354-87 «Передачи зубчатые цилиндрические эвольвентные внешнего зацепления. Расчет на прочность».
2.5.9.1 Проверка зубьев прямозубого колеса по
напряжениям изгиба зубьев
Условие прочности σF ≤ 1,1 [σ ]F, где σF – расчетное (действительное) напряжение изгиба.
Расчетное напряжение изгиба в зубьях колеса
σF2 = 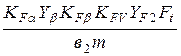 , (2.17)
, (2.17)
где КFα – коэффициент, учитывающий распределение нагрузки между зубьями: для прямозубых колес КFα = 1;
Yβ = 1 – (β°/140) – коэффициент, учитывающий влияние наклона зуба; при β = 0, Yβ = 1;
КFβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий; для приработанных зубьев колес и скорости V ≤ 15 м/с, КFβ = 1;
КFY – коэффициент, учитывающий внутреннюю динамическую нагрузку, принимают для прямозубых колес при твердости зубьев ≤ 350 НВ – 1,4;
YF – коэффициент формы (прочности) зуба, принимают по эквивалентному числу зубьев zV = z/ cos3β, по таблице 21 [Р. 10].
Для шестерни при z1 = 40 YF1 = 3,70;
для колеса z2 = 200 YF2 = 3,59.
Расчетное напряжение изгиба в зубьях шестерни
σF1 =  . (2.18)
. (2.18)
Расчетное напряжение изгиба может отклоняться от допускаемых
σF ≤ 1,1 [σ ]F.
Используя формулы (2.17) и (2.18), получим
σF2 =  Н/мм2;
Н/мм2;
σF1 = 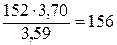 Н/мм2.
Н/мм2.
Условия прочности зубьев по напряжениям изгиба выполняются, так как σF2 = 152 Н/мм2 < [σ]F2 = 256 Н/мм2;
σF1 = 156 Н/мм2 < [σ ]F1 = 294 Н/мм2.
2.5.9.2 Проверка зубьев прямозубого колеса по контактным напряжениям
Условие прочности σН = (0,9...1,05) [σ ]Н.
Расчетное контактное напряжение для прямозубых колес
σН = 436 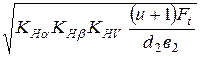 , (2.19)
, (2.19)
где КНα – коэффициент, учитывающий распределение нагрузки между зубьями прямозубых колес КНα = 1,0;
КНβ – коэффициент концентрации нагрузки, для приработанных зубьев колес и скорости V ≤ 15 м/с, КНβ = 1;
КНV – коэффициент динамической нагрузки для прямозубых колес при твердости зубьев ≤ 350 НВ – 1,2; > 350 НВ – 1,1;
u - передаточное число.
Используя формулу (2.19), получим для прямозубой передачи
σН = 436 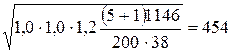 Н/мм2.
Н/мм2.
σН = (0,9...1,05) [σ ]Н = (0,9...1,05) 514 = (462,6…..539,7) Н/мм2.
Условие прочности зубьев по контактным напряжениям выполняется, так как σН = 454 Н/мм2 не превышает допускаемых значений (462,6…539,7) Н/мм2.
Результаты расчета цилиндрической прямозубой передачи приведены в таблице 2.3.
Таблица 2.3
Результаты расчета прямозубой передачи
| Наименование параметров и размерность | Обозначение | Величина |
| Допускаемое контактное напряжение, Н/мм2 | [σ]Н | |
| Допускаемое напряжение изгиба для колеса, Н/мм2 | [σ]F2 | |
| Допускаемое напряжение изгиба для шестерни, Н/ мм2 | [σ]F1 | |
| Межосевое расстояние, мм | а | |
| Модуль передачи (зацепления), мм | m | |
| Число зубьев шестерни | z1 | |
| Число зубьев колеса | z2 | |
| Фактическое передаточное число | uф | |
| Делительный диаметр шестерни, мм | d1 | |
| Делительный диаметр колеса, мм | d2 | |
| Диаметр окружности вершин зубьев шестерни, мм | d а 1 | |
| Диаметр окружности вершин зубьев колеса, мм | d а 2 | |
| Диаметр окружности впадин зубьев шестерни, мм | d f 1 | 37,5 |
| Диаметр окружности впадин зубьев колеса, мм | d f 2 | 197,5 |
| Ширина зубчатого венца шестерни, мм | в 1 | |
| Ширина зубчатого венца колеса, мм | в 2 | |
| Высота головки зуба, мм | h a | |
| Высота ножки зуба, мм | h f | 1,25 |
 Высота зуба, мм Высота зуба, мм
| h | 2,25 |
| Окружной шаг, мм | ρ | 3,14 |
| Толщина зуба, ширина впадины, мм | s = e | 1,57 |
| Радиальный зазор, мм | с | 0,25 |
| Окружная сила, Н | Ft | |
| Радиальная сила, Н | F r | |
| Осевая сила, Н | F а | |
| Расчетное напряжение изгиба, Н/мм2: | ||
| зубьев шестерни | σF1 | |
| зубьев колеса | σF2 | |
| Расчетное контактное напряжение зубьев, Н/мм2 | σH |
2.6 Проектировочный и проверочный расчеты косозубой передачи
2.6.1 Межосевое расстояние
Межосевое расстояние определяется из условия контактной прочности зубьев
σН ≤ [σ]Н.
Межосевое расстояние
а ≥ К а (u +1)  , (2.20)
, (2.20)
где а – межосевое расстояние в мм;
К а – коэффициент межосевого расстояния (для косозубых и шевронных колес К а = 43);
u – передаточное число;
ψ а – стандартное значение коэффициента ширины колес (при симметричном расположении колес относительно опор ψ а = 0,315);
Т2 – вращающий момент в Н·мм;
[σ ]Н – допускаемое контактное напряжение в Н/мм2 (МПа);
КНβ – коэффициент концентрации нагрузки (при НВ≤350 КНβ = 1).
Таким образом, межосевое расстояние
а = 43 (5+1) 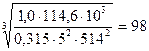 мм.
мм.
Вычисленное межосевое расстояние округляем в большую сторону до стандартного числа (по таблице 1[Р. 10]) а = 100 мм.
2.6.2 Предварительные основные размеры колеса
Делительный диаметр
d'2= 2 а · u /(u + 1) = 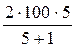 = 166,7 мм,
= 166,7 мм,
ширина колеса в 2 = Ψ а а = 0,315 · 100 = 31,5 мм.
Ширину колеса после вычисления округляем в ближайшую сторону до целого числа, т.е. в 2 = 32 мм.
2.6.3 Модуль передачи
Модуль зацепления является важнейшим параметром зубчатой передачи, он должен быть стандартным, одинаковым для колеса и шестерни, по нему нарезают зубья колес с помощью инструментальной рейки и рассчитывают геометрические параметры колес.
Предварительно модуль передачи определяют по формуле
m' ≥  , (2.21)
, (2.21)
где Кm - коэффициент модуля для косозубых колес = 5,8; шевронных – 5,2;
[σ ]F - допускаемое изгибное напряжение, подставляют меньшее из [σ]F1 и [σ ]F2, т.е. [σ]F = [σ]F2 = 256 Н/мм2 (МПа).
Значение модуля передачи m в мм, полученное расчетом, округляют в большую сторону до стандартного (ГОСТ 9563-80) из ряда чисел (таблица 19 [Р. 10]).
При выборе модуля 1-й ряд следует предпочитать 2-му.
В результате расчета получим модуль передачи косозубого зацепления
m' =  мм.
мм.
Принимаем стандартное значение m = 1 мм.
2.6.4 Числа зубьев косозубых колес
Суммарное число зубьев косозубых и шевронных колес
zΣ = 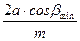 . (2.22)
. (2.22)
Минимальный угол наклона зубьев:
косозубых колес
βmin = arc sin 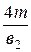 ; (2.23)
; (2.23)
шевронных колес βmin = 25°.
Полученное значение zΣ округляют в меньшую сторону до целого и определяют действительное значение угла β, с точностью вычисления до четвертого знака после запятой
β = аrc cos 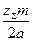 . (2.24)
. (2.24)
Для косозубых колес β = 8…18°.
Число зубьев шестерни
z1 =  . (2.25)
. (2.25)
Значение z1 округляют в ближайшую сторону до целого:
z1min = 17cos3β – для косозубых и шевронных колес.
Число зубьев колеса
z2 = zΣ – z1.
В результате вычислений получаем:
минимальный угол наклона зубьев косозубых колес
βmin = arc sin 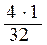 = 7,18°;
= 7,18°;
суммарное число зубьев косозубых колес
zΣ = 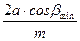 =
= 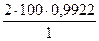 = 198,4, принимаем zΣ =198.
= 198,4, принимаем zΣ =198.
Не нашли, что искали? Воспользуйтесь поиском: