
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Червячным редуктором 4 страница
ω2 = 41,9 с-1;
ресурс работы: t = Lh = 30000 часов.
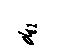  |
Рис. 3.1 Расчетная схема конической передачи
    |
Рис. 3.2 Геометрические параметры шестерни и колеса
3.2 Выбор материала и термической обработки колес
Материалы для изготовления зубчатых колес выбирают в зависимости от условий эксплуатации, требований к габаритам передачи, технологии изготовления и с учетом экономических показателей. Применяют как среднеуглеродистые, так и высокоуглеродистые стали с различными вариантами термообработки: улучшение, закалка токами высокой частоты (ТВЧ), цементация.
Термическая обработка повышает твердость рабочей поверхности зубьев, которая определяется в единицах Бринелля (НВ). При твердости НВ > 350 твердость материала измеряется по шкале Роквелла (HRC). Твердость HRC переводится в твердость НВ по таблице 16 [Р. 10] или по приближенному соотношению 10 НВ ≈1 HRC.
Чем выше твердость рабочей поверхности зубьев, тем выше допускаемые контактные напряжения [σ]Н и тем меньше размеры передач, но сложнее технология изготовления колес и выше стоимость.
Так как в задании нет особых требований в отношении габаритов передачи, выбираем широко применяемые недорогие материалы (таблица 16 [Р. 10]): для колеса - сталь марки 40X, термообработка колеса – улучшение, твердость поверхности 269..302 НВ; для шестерни – сталь 40X, термообработка –улучшение и закалка ТВЧ, твердость поверхности зубьев 45..50 HRC.
Средняя твердость определяется по формуле:
НВср = 0,5 (НВmin + НВmax), (3.1)
для колеса НВср = 0,5(269+302) = 285,5;
для шестерни НRCср = 0,5(45+50)=47,5 или НВср=450.
3.3 Допускаемые контактные напряжения
Допускаемые контактные напряжения определяются отдельно для колеса [σ]Н2 и шестерни [σ]Н1 по формуле:
[σ]Н = КНL[σ]HO, (3.2)
где КНL - коэффициент долговечности;
[σ]HO - допускаемые напряжения, соответствующие базовым числам циклов нагружений.
Коэффициент долговечности при расчете по контактным напряжениям определяется по формуле:
KHL = 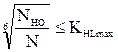 ; (3.3)
; (3.3)
где NHO - базовое число циклов нагружения;
N – действительное число циклов перемены напряжений;
KHLmax – максимальноe значение коэффициента долговечности (при ТО улучшение КHLmax= 2,6; при ТО закалка KHLmax = 1,8).
Базовые числа циклов нагружения NHOопределяются в зависимости от твердости по формуле:
NHO= (HBср)3,(3.4)
для колеса NHO2 = (285,5)3 = 2,3∙107, для шестерни NHO1=(450)3=9,1∙107.
Действительные числа нагружений определяются по следующим формулам: для колеса N2 = 60 ∙ n2 ∙ t = 60 ∙ 400 ∙ 30000 = 7,2∙108;
для шестерни N1 = N2∙u = 7,2 ∙ 108 ∙ 2,38 = 17∙108.
Если N > NHO, то коэффициент долговечности KHL = 1,0.
Допускаемые напряжения контактной выносливости зубьев для колеса и шестерни находим по формулам из таблицы 17 [Р.10] в зависимости от материала и твердости.
Для колеса
[σ]HO2 = 1,8 HBср + 67 = 1,8∙285,5+ 67 = 581 Н/мм2,
для шестерни с большей твердостью другая формула
[σ]HO1 = 14НRСср + 70 = 735 Н/мм2.
С учетом этих значений, при KHL = 1, допускаемые контактные напряжения будут иметь следующие значения: [σ]HO2=581Н/мм2; [σ]HO1 =735 Н/мм2. Для дальнейших расчетов принимаем меньшее из значений [σ]H2, [σ]H1, т.е. [σ]H = 581 Н/мм2.
3.4 Допускаемые изгибные напряжения
Допускаемые напряжения изгиба определяются отдельно для колеса [σ]F2и шестерни [σ]F1по формуле:
[σ]F = KFL[σ]FO, (3.5)
где [σ]FO - допускаемые предельные напряжения изгибной выносливости зубьев, соответствующие базовым числам циклов нагружений при расчете на изгиб NFO = 4∙ 106, выбираются по таблице 17[4] в зависимости от средней твердости колес HBср.
Для нашего случая: [σ]FO =1,03НВср.
KFL - коэффициент долговечности при расчете на изгиб, KFL = 1,0 при
N ≥ 4 ∙ 106; при других значениях Nрассчитывается по формуле:
KHL =  ≤ KFLmax, (3.6)
≤ KFLmax, (3.6)
где m - показатель степени, m = 6 при ТО улучшение и m = 9 при ТО закалка.
Максимальное значение коэффициента KFLmax при ТО улучшение KFLmax= 2,08; при ТО закалка KFLmax= 1,63.
Так как действительные числа циклов перемены напряжений:
N2 = 720∙106 > 4∙ 106, то KFL2 = 1,0;
N1 = 2600 ∙ 106 > 4∙ 106, то KFL1 = 1,0.
Допускаемые изгибные напряжения для колеса и шестерни определяются по формулам:
[σ]F1= KFL1 [σ]FO1 = 1,03∙450 = 464 Н/мм2;
[σ]F2 = KFL2[σ]FO2 = 1,03∙285,5 = 294 Н/мм2.
Для дальнейших расчетов принимается: [σ]F2 = 294 Н/мм2 и [σ]F1 = 464 Н/мм2.
3.5 Проектировочный расчет конической прямозубой передачи
3.5.1 Диаметр внешней делительной окружности колеса
Предварительный диаметр внешней делительной окружности колеса определяется из условия контактной прочности зубьев:
d'e2 ≥ 165 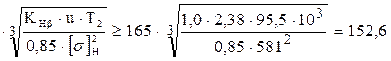 мм (3.7)
мм (3.7)
где KHβ = 1,0 - коэффициент концентрации нагрузки;
u - передаточное число;
[σ]H- допускаемое контактное напряжение, Н/мм2 (МПа);
T2 - вращающий момент, H·мм.
3.5.2 Углы делительных конусов шестерни и колеса, конусное
расстояние и ширина колес
Углы при вершинах делительных конусов шестерни δ1 и колеса δ2 определяютсяпо формулам (таблица 24 [Р. 10]):
δ2 = arctg u = arctg 2,38 = arctg(0,42) = 67,2°;
δ1 = 90º - δ2 = 90º - 67,2° = 22,8°. (3.8)
Конусное расстояние колес:
Re = 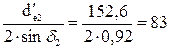 мм. (3.9)
мм. (3.9)
Ширина зубчатого венца колес b:
b = 0,285∙Re = 0,285∙83 = 23,7 мм. (3.10)
Округляя полученное значение до целого, принимаем b = 24 мм.
3.5.3 Модуль передачи
Внешний окружной модуль передачи рассчитывается по формуле:
me ≥  ,
,
где [σ]F2 - допустимое изгибное напряжение колеса;
KFβ = 1 - коэффициент концентрации нагрузки для прирабатывающихся прямозубых колёс;
T2 - вращающий момент на выходном валу, Н∙мм;
d'e2- диаметр внешней делительной окружности колеса, мм.
Полученное значение модуля округляется в большую сторону до ближайшего стандартного значения, приведенного в таблице 19 [4], т.е. me = 1,5 мм.
3.5.4 Число зубьев конических колес
Число зубьев колеса определяется по формуле:
z2 =  . (3.12)
. (3.12)
Полученное число зубьев округляется в ближайшую сторону до целого числа: z2 = 102.
Число зубьев шестерни определяется по формуле:
z1 = 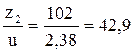 . (3.13)
. (3.13)
полученное значение числа зубьев шестерни округляется в ближайшую сторону до целого числа z1 = 43.
3.5.5 Фактически передаточное число
Фактически передаточное число:
uф = 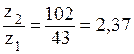 . (3.14)
. (3.14)
Отклонение от заданного передаточного числа не должно быть больше 4%, т.е.
∆ u = 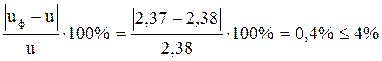 .
.
3.5.6 Размеры колес конической передачи
Размеры конического колеса передачи и шестерни показаны на рис. 3.2.
Углы делительных колес конусов колеса δ2 и шестерни δ1:
δ2 = arctg(uф) = arctg(2,37) = 67°;
δ1 = 90º - δ2 = 90º - 67° = 23°. (3.15)
Делительные диаметры шестерни de1 и колеса de2:
de1 = me ∙ z1 = 1,5 ∙ 43 = 65 мм;
de2 = me ∙ z2 = 1,5 ∙ 102 = 153 мм. (3.16)
Коэффициенты смещения шестерни и колеса:
хе1 = 2,6 ∙u0,14 ∙ z1-0,67 = 2,6 ∙2,370,14 ∙43-0,67 = 0,235;
хе2 = - хе1 = - 0,235. (3.17)
С учетом коэффициентов смещения внешние диаметры шестерни dae1и колеса dae2 равны:
dae1 = de1 + 2(1+xe1)∙me ∙ cosδ1 = 65 +2(1+0,235)∙1,5∙0,941 = 68 мм;
dae2 = de2 + 2(1+хе2)∙me ∙ cosδ2 = 153 + 2(1-0,235)∙1,5∙0,495 = 154 мм. (3.18)
3.5.7 Силы в зацеплении
При определении сил, действующих в прямозубом зацеплении, результирующую силу Fnна среднем делительном диаметре колеса, нормальную к поверхности зуба, раскладывают на составляющие: окружную силу Ft, радиальную Fr, осевую Fa. Схема сил в зацеплении для конической передачи приведена на рис. 3.3.
Окружная сила на среднем диаметре колеса равна окружной силе на шестерне  :
:
Ft2 = 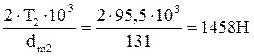 . (3.19)
. (3.19)
где dm2 – средний диаметр колеса,
dm2 = 0,857 ∙ de2 = 0,857∙153 = 131 мм.
Осевая сила на шестерне, равная радиальной силе на колесе:
Fa1 = Fr2 = Ft ∙ tgα ∙sin δ1 = 1458∙0,364∙0,339 = 180 H. (3.20)
Радиальная сила на шестерне, равная осевой силе на колесе:
Fr1 = Fa2 = Ft ∙ tgα ∙ cos δ1 = 1458 ∙ 0,364 ∙ 0,941 = 499 H, (3.21)
где tgα = tg 20º = 0,364.
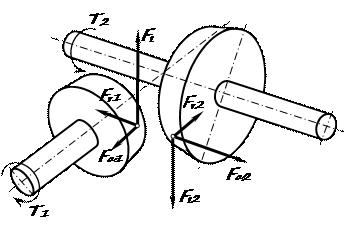 |
Рис. 3.3 Силы в зацеплении конической передачи
3.5.8 Степень точности зацепления
Степень точности передачи определяют по таблице 20 [Р.10], в зависимости от окружной скорости колеса
V = 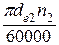 , м/с.
, м/с.
Окружная скорость колеса
V = (3,14·153·400) /60000 = 3,2 м/с.
По окружной скорости определяем 8-ю степень точности зацепления.
3.6 Проверочный расчет зубьев конического колеса
3.6.1 Проверка зубьев конического колеса по напряжениям изгиба
Условие изгибной прочности:
σF ≤ 1,1 [σ]F, (3.22)
где [σ]F - допускаемое напряжение изгиба.
Расчетное напряжение изгиба в зубьях колеса вычисляются по формуле:
σF2 = 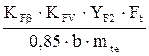 , (3.23)
, (3.23)
где KFβ = 1 - коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий, для приработанных зубьев колес;
KFV- коэффициент, учитывающий внутреннею динамическую нагрузку, для прямозубых колес при твердости зубьев ≤ 350НВ, KFV = 1,4; при < 350 HB, KFV = 1,2.
YF1 и YF2 - коэффициенты формы зуба (таблица 21[Р. 10]), определяемые по эквивалентному числу зубьев.
Эквивалентные числа зубьев:
zV1 = 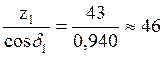 ,
,
zV2 = 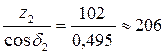 . (3.24)
. (3.24)
По таблице 21 [Р. 10], находим: YF1 = 3,66 и YF2 = 3,61.
Расчётное напряжение изгиба в зубьях колеса:
σF2 = 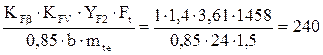 Н/мм2 .
Н/мм2 .
Расчетное напряжение изгиба в зубьях шестерни:
σF1 = σF2∙  . (3.25)
. (3.25)
Полученные напряжения меньше допускаемых: [σ]F2 = 294 Н/мм2 и [σ]F1 = 464 Н/мм2, таким образом условия прочности по напряжениям изгиба выполняются.
3.6.2 Проверка зубьев конического колеса по
контактным напряжениям
Условие контактной прочности зубьев:
σН = (0,9…1,1)∙ [σ]Н. (3.26)
Расчетное контактное напряжение вычисляется по формуле:
σН = 2,12 ∙ 103 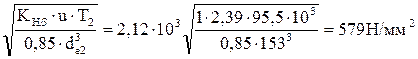 , (3.27)
, (3.27)
где KHβ = 1 - коэффициент концентрации нагрузки для приработанных зубьев колес.
Интервал допускаемых контактных напряжений:
σH = (0,9…1,1)∙[σ]H = (0,9…1,1)∙581 = (523…639)Н/мм2.
Таким образом, условие контактной прочности зубьев выполняется. При несоблюдении условия контактной прочности зубьев, изменяют диаметр колеса  .
.
Результаты расчета прямозубой конической передачи приведены в таблице 3.1.
Таблица 3.1
Результаты расчета прямозубой конической передачи
| Наименование параметров и размерность | Обозначение | Величина |
| Допускаемое контактное напряжение, Н/мм2 | [σ]Н | |
| Допускаемое напряжение изгиба для колеса, Н/мм2 | [σ]F1 | |
| Допускаемое напряжение изгиба для шестерни, Н/мм2 | [σ]F2 | |
| Модуль передачи (зацепления), мм | me | 1,5 |
| Число зубьев шестерни | z1 | |
| Число зубьев колеса | z2 | |
| Фактическое передаточное число | uф | 2,37 |
| Делительный диаметр шестерни, мм | de1 | |
| Делительный диаметр колеса, мм | de2 | |
| Внешний диаметр шестерни, мм | dae1 | |
| Внешний диаметр колеса, мм | dae2 | |
| Конусное расстояние колеса, мм | Re | |
| Ширина зубчатого венца колеса, мм | b | |
| Угол делительных конусов шестерни, градус | δ1 | |
| Угол делительных конусов колеса, градус | δ2 | |
| Окружная сила, Н | Ft1 = Ft2 | |
| Радиальная сила на шестерне, равная осевой силе на колесе, Н | Fr1 = Fa2 | |
| Осевая сила на шестерне, равная радиальной силе на колесе, Н | Fa1 = Fr2 | |
| Расчетное напряжение изгиба зубьев шестерни: Н/мм2 | σF1 | |
| Расчетное напряжение изгиба зубьев колеса: Н/мм2 | σF2 | |
| Расчетное контактное напряжение зубьев, Н/мм2 | σН | |
| Средний диаметр колеса, мм | dm2 |
3.7 Эскизное проектирование конической передачи
При эскизном проектировании определяют ориентировочные диаметры валов, выбирают типы подшипников и схемы их установки, составляют эскизную компоновку деталей передач.
3.7.1 Проектировочный расчет входного вала
3.7.1.1 Расчетная схема. Исходные данные
Валы передач, как правило, изготавливаются ступенчатыми, что позволяет строго балансировать детали на валу в осевом направлении, упрощать сборку, обеспечивать посадку деталей и т.п.
Входной вал передачи, как правило, представляет собой "вал-шестерню" и имеет концевой участок, участки для установки подшипников, буртики для подшипников, участки для нарезания зубьев шестерни.
Валы конструируются по возможности гладкими, с минимальным числом уступов, что приводит к существенному сокращению материала при изготовлении.
На рис. 3.7.1 представлена расчетная схема входного вала, который выполнен заодно с конической шестерней (вал-шестерня).
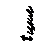       |
Рис. 3.7.1 Расчетная схема входного вала
Исходные данные:
вращающий момент на входном валу Т1 = 42,26 Н·м;
внешний диаметр шестерни dae1 = 68 мм;
внешний диаметр колеса dае2 = 154 мм.
3.7.1.2 Геометрические размеры входного вала
Минимальный размер концевого участка вала d, определяется из условий прочности на кручение по пониженному допускаемому касательному напряжению [τ] = 15… 30 Н/мм2:
d = 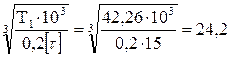 мм.
мм.
После округления до стандартной величины, принимаем d = 24 мм.
Диаметр промежуточного участка – d1 определяется по формуле:
d1 = d + 2 · tцил = 24 + 2 · 3,5 = 31 мм,
где tцил = 3,5 мм определяется по таблице 35 [Р. 10] в зависимости от значения d.
Диаметр резьбового участка – d2, на который навинчивается гайка для упора внутренней обоймы подшипника, выбирается в диапазоне:
d2 = d1 + (2…4) мм = 31 + (2…4) = (33…35) мм,
по стандартному значению метрической резьбы: d2 = 35 мм(резьба М35).
Диаметр вала под подшипники – dП выбирают по значению: dП ≥ d2.
Выбранный диаметр dП округляется до значения кратного 5,
dП = 35 мм.
Так как в зацеплении конических передач действуют окружная Ft, радиальная Fr и осевая Fa силы, то выбираем подшипники роликовые конические однорядные (ГОСТ 333 - 79). По значению dП = 35 мм из таблицы 40 [Р. 10] выбираем подшипник легкой серии для входного вала № 7207, ширина подшипника Т = 18,25 мм.
Диаметр буртика под подшипники – dБП:
dБП = dП + 3 · r = 35 + 3 · 2 = 41 мм,
где r = 2 мм определяется по таблице 35 [Р. 10] в зависимости от значения d.
Линейные размеры соответствующих участков вала:
длина посадочного конца вала
ℓМБ = 1,5·d = 1,5 · 24 = 36 мм;
длина промежуточного участка
ℓКБ = 0,8∙d1 = 0,8∙31 = 24,8 мм;
длина резьбового участка
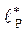 = 0,4 ∙ d2 = 0,4∙35 = 14 мм;
= 0,4 ∙ d2 = 0,4∙35 = 14 мм;
длина участка вала под подшипник
ℓП = ℓР + Т = 46,2 + 18,25 = 64 мм,
где ℓР = 0,3 ∙ dае2 = 0,3 ∙ 154 = 46,2 мм - рабочая длина, по которой ведётся расчет на прочность и жёсткость вала.
Длина вала-шестерни:
ℓ1 = ℓМБ + ℓКБ +  + ℓР + Т + b = 36 + 24,8 + 14 + 18,25 + 46,2 + 24 =
+ ℓР + Т + b = 36 + 24,8 + 14 + 18,25 + 46,2 + 24 =
= 163,2 мм. Принимаем ℓ1 = 164 мм.
Другие размеры вала, включая общую длину, выявляются при вычерчивании компоновочного эскиза передачи.
3.7.2 Проектировочный расчет выходного вала
3.7.2.1 Расчетная схема. Исходные данные
Расчетная схема выходного вала представлена на рис. 3.7.2.
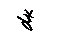  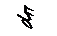    |
Рис. 3.7.2 Расчетная схема выходного вала
Исходные данные:
вращающий момент на выходном валу Т2 = 95,5 Н∙м;
внешний диаметр колеса dae2 = 154 мм;
ширина колеса в = 24 мм.
3.7.2.2 Геометрические размеры выходного вала
Из условий прочности на кручение по пониженным допускаемым касательным напряжениям минимальный диаметр концевого участка вала определяем по формуле:
d = 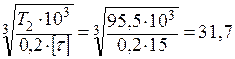 мм,
мм,
диаметр вала округляем в большую сторону до стандартного числа по таблице 1 [Р. 10], d = 32 мм.
Диаметр вала под подшипники
dП = d + 2 ∙tцил = 32 + 2 ∙ 3,5 = 39 мм,
где tцил= 3,5 мм определяется по таблице 35[Р. 10] в зависимости от значения d.
Полученный диаметр dП округляется до значения кратного 5, dП = 40 мм. Так как в зацеплении конических передач действуют окружная Ft, радиальная Frи осевая Fa силы, то выбираем подшипники роликовые конические однорядные (ГОСТ 333 - 79). По значению dП = 40 мм для выходного вала из таблицы 40[Р. 10] выбираем подшипник легкой серии №7208, ширина подшипника Т = 19,25 мм.
Диаметр вала под колесом:
dК = dП + 3∙ r = 40 + 3 ∙2,5 = 47,5 мм,
где r = 2,5 мм определены по таблице 35 [Р. 10] в зависимости от значения d.
Диаметр буртика вала для колеса:
dБК = dК + 3 ∙ f = 47,5 + 3 ∙ 1,2 = 51,1 мм,
где f определяется по таблице 35 [Р. 10] в зависимости от значения d.
Распорная втулка устанавливается либо на одном диаметре с колесом dК, либо на диаметре на 1-2 мм меньше dК.
При выборе линейных размеров различных участков вала рекомендуется придерживаться следующих значений:
длина концевого участка:
ℓМТ = 1,5 ∙ d = 1,5 ∙ 32 = 48 мм;
длина промежуточного участка:
ℓКТ = 1,2 ∙ dП = 1,2 ∙ 40 = 48 мм.
Чтобы поверхности вращающихся колес не задевали за внутренние поверхности стенок корпуса, между ними оставляется зазор а (рис. 3.7.3), определяемый по формуле:
а =  + 3 =
+ 3 = 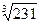 + 3 ≈ 9 мм,
+ 3 ≈ 9 мм,
где L ≈ 1,5 dае2 = 1,5 · 154 = 231 мм. Принимаем а = 9 мм.

Рис. 3.7.3 Схема компоновки редуктора
Длина вала колеса зависит от конструкции конического зубчатого колеса и окончательно определяется при вычерчивании эскиза передачи; здесь можно лишь определить ориентировочные его размеры: ℓК > dae1 + a, чтобы можно было разместить коническую шестерню; ℓК > ℓСТ + а,
гдеℓСТ – длина ступицы колеса:
ℓСТ = 1,2 ∙dК = 1,2 ∙ 47,5 = 57 мм,
(окончательно ℓСТ определяется по расчетам шпоночного соединения вала и ступицы конического колеса);
ℓК ≈ da1 + a + 2 ∙ ℓСТ = 68 + 9 + 2 ∙57 = 191 мм.
Расчетная длина вала, необходимая для расчета на статическую и усталостную прочность вала:
ℓР = ℓК + Т + а = 191 + 19,25 + 9,0 = 219,25 мм.
Принимаем ℓР = 220 мм.
Длина выходного вала:
ℓ2 = ℓр + ℓКТ + ℓМТ = 220 + 48 + 48 = 316 мм.
Принимаем ℓ2 = 316 мм.
3.7.3 Выбор подшипников для валов
В конструкции конической зубчатой передачи необходимо использовать конические роликовые подшипники, так как в такой передаче возникают и осевые усилия.



 Первоначально были выбраны роликовые конические однорядные подшипники легкой серии, геометрические параметры такого подшипника показаны на рис. 3.7.4. Номера подшипников выбраны по значению диаметра вала под подшипники (dП). Для входного вала выбран подшипник №7207, для выходного - №7208. Из таблицы 40 [Р. 10] выписываем основные характеристики подшипников.
Первоначально были выбраны роликовые конические однорядные подшипники легкой серии, геометрические параметры такого подшипника показаны на рис. 3.7.4. Номера подшипников выбраны по значению диаметра вала под подшипники (dП). Для входного вала выбран подшипник №7207, для выходного - №7208. Из таблицы 40 [Р. 10] выписываем основные характеристики подшипников.
Не нашли, что искали? Воспользуйтесь поиском: