
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Пересечение двух плоскостей
В этой позиционной задаче общим элементом данных геометрических объектов является прямая линия. Её можно построить двумя способами: с помощью плоскостей-посредников частного положения, одновременно пересекающих обе данные плоскости и способом на основе пересечения прямой линии с плоскостью.
 |
Рисунок 1.3.25 – Пересечение двух плоскостей общего положения
Пример построения линии пересечения двух плоскостей способом секущих плоскостей посредников представлен на рисунке 1.3.25. Плоскость S определяется пересекающимися прямыми а и b, а плоскость Q – параллельными прямыми с и d.
Для нахождения линии l пересечения плоскостей S и Q проведём две фронтально проецирующие плоскости W (W2) и W¢ (W¢2), являющиеся посредниками. Плоскость W пересекает данные плоскости S и Q по прямым линиям 1-2 (12-22, 11-21) и 3-4 (32-42, 31-41). Точку пересечения этих прямых обозначим через К (К1, К2). Точка К принадлежит одновременно трём плоскостям S, Q, W. Следовательно, точка К принадлежит линии пересечения плоскостей S и Q. Плоскость W¢ пересекает плоскости S и Q по прямым линиям 5-6 (51-61, 52-62) и 7-8 (71-81, 72-82). Точкой пересечения этих линий является точка К¢. Она, как и точка К принадлежит линии пересечения плоскостей S и Q. Следовательно, прямая l, проходящая через точки К и К¢, есть искомая прямая пересечения данных плоскостей S и Q.
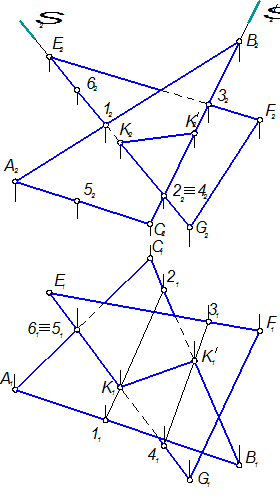 |
Рисунок 1.3.26 – Пересечение двух плоскостей общего положения
На рисунке 1.3.26 представлен пример построения линии пересечения двух плоскостей способом пересечения прямой линии с плоскостью. Плоскости заданы треугольниками АВС и EGF. Вспомогательные секущие плоскости S (S2) и S¢ (S2) проведены через стороны EG и ВС треугольников. Плоскость S (S2) пересекает треугольник АВС по прямой 1-2. Точка К является результатом пересечения прямых EG и 1-2. Плоскость S¢ (S¢2) пересекает треугольник EGF по прямой 3-4. Точка К¢ является результатом пересечения прямых ВС и 3-4. Точки К и К¢ ограничивают отрезок искомой линии пересечения, находящийся в пределах обоих треугольников.
Относительная видимость треугольников определена на фронтальной проекции с помощью конкурирующих точек 2 и 4, из которых точка 4 стороны EG закрывает собой точку 2 стороны ВС. Видимость на горизонтальной плоскости проекций определена с помощью конкурирующих точек 5 и 6, из которых точка 6 стороны EG закрывает собой точку 5 стороны АС.
Кривые линии
Кривую линию можно рассматривать как след движущейся точки. Эта точка может быть отдельной точкой или точкой, принадлежащей движущейся в пространстве линии или поверхности.
Кривые линии могут быть образованы пересечением кривой поверхности плоскостью (в общем случае), взаимным пересечением двух поверхностей, из которых хотя бы одна является кривой.
Законом образования кривой линии называется совокупность условий, определяющих эту линию. Точка, линия, поверхность перемещаются в пространстве, подчиняясь разным условиям. Плоскость может пересекать разнообразные кривые поверхности по самым различным направлениям. Взаимно пересекаться могут самые разнообразные поверхности при различном положении их относительно друг друга. Отсюда следует, что образование кривой линии может подчиняться бесчисленному множеству условий и может быть образовано бесчисленное множество кривых линий. Кроме того, одна и та же кривая линия может быть образована различными способами.
Например, эллипс может быть образован движением точки в плоскости, при котором в каждый данный момент сумма расстояний от этой точки до двух других неподвижных точек – фокусов эллипса – постоянна и равна большой оси эллипса. Но эллипс может быть образован и пересечением кругового цилиндра с плоскостью, расположенной произвольно по отношению к его оси или полным пересечением поверхностей двух круговых цилиндров одинакового диаметра.
Все кривые линии по положению их точек в пространстве делятся на два вида: плоские кривые – кривые, все точки которых лежат в одной плоскости (например, окружность, эллипс, парабола и т.д.) и пространственные кривые – кривые, точки которых не лежат в одной плоскости, например, винтовая линия
Не нашли, что искали? Воспользуйтесь поиском: