
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Образование, задание и изображение поверхностей
Начертательная геометрия пользуется преимущественно кинематическим способом образования поверхностей. Это означает, что поверхность образуется непрерывным перемещением линии (образующей) в пространстве по определённому закону. Тогда и сама поверхность будет непрерывной. Образующая может или сохранять свою форму при изменении положения, или непрерывно изменять и форму, и положение в пространстве.
Принадлежность поверхности некоторому классу описывается такими элементами, которые однозначно определяют её форму и размеры.
Совокупность элементов поверхности (параметров), выделяющих данную поверхность из всего класса поверхностей, к которому она принадлежит, будем называть определителем поверхности.
Например, конус вращения полностью задаётся осью и образующей в соответствии с рисунком 1.3.31. Поэтому определитель конической поверхности Q будет записан так: Q (i,l).
Задание оси i и образующей l конуса вращения позволяет построить этот конус. На нём можно провести любую другую прямолинейную образующую (l1,l2,…) или окружность (q,m) поверхности, а также отметить произвольную её точку (М). Заметим, что этот способ задания конуса не является единственным.
 |
Исходя из определителя поверхности конуса вращения, для задания конуса на чертеже достаточно задать проекции элементов определителя: i (l1,i2) и l (l1,l2) в соответствии с рисунком 1.3.32. Такой способ графического задания поверхности является метрически определённым и позволяет решать любые задачи на поверхности, а также её реконструировать.
Рисунок 1.3.31 – Конус вращения
Закон перемещения в пространстве кривой (образующей), описывающий поверхность, удобно задавать некоторыми неподвижными кривыми, по которым скользит движущаяся образующая. Эти кривые, называемые направляющими линиями, часто входят в состав определителя поверхности.
Таким образом, на любой кинематической поверхности можно выделить два семейства кривых линий: семейство образующих (l) и семейство направляющих (m), каждое из которых покрывает всю поверхность и состоит из каких-либо линий (плоских или пространственных) в соответствии с рисунком 1.3.33.
Если поменять местами образующие и направляющие, т.е. принять m за образующие, а l – за направляющие, то в результате получится та же поверхность W.
Из кривых l1,l2… и m1,m2…, принадлежащих к указанным двум семействам линий, может быть составлен каркас кинематической поверхности.
Если учесть непрерывность перемещения образующей, а, следовательно, и непрерывность самой поверхности, то можно сделать очень важный для теории кинематических поверхностей вывод о том, что через любую точку поверхности можно провести пару кривых, принадлежащих двум различным семействам линий на поверхности.
Простейшей и основной задачей, входящей в виде элемента в решение любой более сложной задачи, является построение проекций точки, принадлежащей поверхности.
 |
Рисунок 1.3.32 – Задание конуса вращения элементами определителя
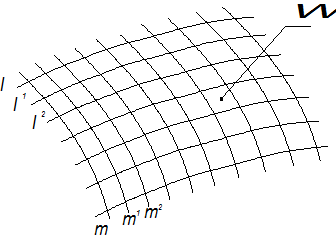 |
Рисунок 1.3.33 – Каркас поверхности
Общий метод заключается в том, что для построения второй проекции, например, М2 точки М, лежащей на поверхности и заданной проекцией М1, проводят через эту проекцию точки М линию l (l1), принадлежащую одному из семейств линий на поверхности. Затем строят вторую проекцию l2 этой линии и проводят через точку М1 линию связи. Вторая проекция М2 точки М будет лежать в пересечении проведённой линии связи с линией l2. Выбор линии того или другого семейства основывается на графической простоте этой линии. На рисунке 1.3.32 использована прямолинейная образующая l¢.
Задание на чертеже кинематических поверхностей, определяемых несколькими точками или линиями, сводится к заданию проекций этих точек и линий. При этом надо иметь в виду некоторые условия, дополняющие чертёж.
Рассмотрим, например, образование поверхности цилиндра вращения. Определитель этой поверхности Q в соответствии с рисунком 1.3.34, а состоит из оси i (i1,i2) и образующей l (l1,l2): Q (i,l).
Цилиндр может быть образован также вращением кривой b, лежащей на его поверхности, или поступательным перемещением окружности m: m1,m2,m3 …(поверхность переноса). В этих случаях определитель должен быть обозначен: Q (i,b), Q (i,m).
Кинематическая поверхность может быть образована также движением образующей поверхности, а не линии, как это было до сих пор. При этом движущаяся поверхность образует множество поверхностей, называемое семейством.
Из дифференциальной геометрии известно, что поверхность, касающаяся в каждой своей точке некоторой поверхности данного семейства, называется огибающей данного семейства.
Так, цилиндр вращения может быть образован как огибающая однопараметрического семейства сфер (L1, L2, L3 …) с центрами О1, О2, О3 …, расположенными на прямой i – оси цилиндра (рисунок 1.3.34, б).
 |
Рисунок 1.3.34 – Способы образования цилиндра вращения
Этот цилиндр будет касаться сфер по окружностям больших кругов (m1,m2,m2…), называемых характеристиками. Определитель поверхности
Q (i, RL), где RL – радиус образующей сферы.
На практике из всех возможных способов образования поверхности и вида образующих линий выбирают наиболее простые и удобные для решения задач.
Одним из основных требований, предъявляемых к чертежам в начертательной геометрии, наряду с обратимостью чертежа является его наглядность. Графическое задание поверхности проекциями элементов её определителя обеспечивает обратимость чертежа, но не обеспечивает его наглядности. Поэтому для увеличения наглядности изображения поверхности во многих случаях указывают на чертеже наряду с проекциями определяющих поверхность точек и линий также и очертание поверхности на плоскостях проекций.
Предположим, что некоторая произвольная поверхность W проецируется на плоскость проекций П¢ в соответствии с рисунком 1.3.35. Тогда можно выделить те проецирующие лучи, которые будут касаться поверхности W и образовывать некоторую проецирующую цилиндрическую поверхность.
Линия l касания проецирующей поверхности и заданной называется контурной линией. Линия l¢ пересечения проецирующей поверхности с
плоскостью П¢ называется очертанием данной поверхности W.
Очертание поверхности получается, таким образом, как проекция контурной линии на данную плоскость проекций.
Очертание поверхности является границей видимости частей поверхности на данной плоскости. Оно отделяет область расположения проекций точек поверхности от всех других точек плоскости проекций. Поэтому при изображении поверхности на комплексном чертеже проекцию контурной линии на других плоскостях будем называть линией видимости.
 |
Рисунок 13.35 – Очертание поверхности
 |
На рисунке 1.3.36 изображена в двух проекциях сфера, очертания которой на плоскостях проекций П1 и П2 есть окружности q1 и m2. На другие плоскости проекций эти окружности проецируются в виде линий видимости q2 и m1 соответственно.
Рисунок 1.3.36 – Очертания и линии видимости сферы
На практике в различных областях техники получили широкое распространение следующие классы кинематических поверхностей:
1) поверхности вращения, которые образуются вращением произвольной
образующей вокруг неподвижной оси, в частности, поверхности вращения
второго порядка;
2) поверхности второго порядка общего вида;
3) линейчатые поверхности, которые могут быть образованы движением
прямолинейной образующей;
4) винтовые поверхности, образуемые винтовым движением произвольной
образующей, и, в частности, линейчатые винтовые поверхности – геликоиды;
5) циклические поверхности, которые могут быть образованы движением
окружности постоянного или переменного диаметра.
Следует отметить, что отдельные поверхности могут быть отнесены не к одному, а к нескольким классам.
Не нашли, что искали? Воспользуйтесь поиском: