
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Лекция 6. Анализ и синтез информационных систем. 2 страница
(1,еслисущест вует пуг ьизвершиньйввершину]сучет омпромеж уг очных;] Si] = < >
[0 -впрот ивномслучае. J
| S = |
Число промежуточных вершин не должно превышать (N -1). Для рассматриваемого
графа S = R:
1111 0111 0010 0111
Структура ИС характеризуется наличием обратных связей. Чтобы выяснить такие связи, строится матрица циклических соединении К: К = S n ST
| R |
Элемент данной матрицы Ц = 1, если существуют пути из вершины I в вершину j и обратно:
1, еслисущест вуют пут иизве ршиньпвве ршинуj иоб рат но; 0 - впрот ивномслучае.
| = К = |
1000 0101 0010 0101
Бинарное отношение, которое связано с матрицей К, задает отношение эквивалентности. По этому отношению можно разбивать вершины на некоторые классы (непересекающиеся множества) эквивалентности. Смысл выделения классов эквивалентности в том, что классы эквивалентности помогают оптимизировать структуру системы. В рассматриваемом примере во втором классе эквивалентности имеются две вершины (2 и 4), которые имеют взаимную обратную связь. Это будет учтено при оптимизации организационной структуры системы.
6.6 Задача оптимизации структур.
Пусть имеется некоторая структура, которая содержит п подразделений для обработки информации экономического характера. Предположим, что каждое подразделение разрабатывает один показатель, а всего на дочернем предприятии осуществляется разработка m показателей.
Тогда можно распределение показателей по подразделениям записать в виде функции отображения R1:
|1,еслипоказат елывычисляет сявпод разделений 1 lj |о — вирот ивномслучае. J
Для вычисления показателей 6.7. Интеллектуализация информационных систем.
Интеллектуальные системы, или системы, основанные на знаниях (Knowledge Based System) - поддерживают задачи принятия решения в сложных системах, где необходимо использование знаний в достаточно широком диапазоне, особенно в плохо формализуемых и плохо структурируемых системах, нечетких системах и при нечетких критериях принятия решения; эти системы наиболее эффективны и применяемы для сведения проблем долгосрочного, стратегического управления к проблемам тактического и краткосрочного характера, повышения управляемости, особенно в условиях многокритериальности. В отличие от экспертных систем, в системах, основанных на знаниях, следует по возможности избегать экспертных и эвристических процедур и прибегать к процедурам минимизации риска. Здесь более существенно влияние профессионализма персонала, ибо при разработке таких систем необходимо сотрудничество и взаимопонимание не только разработчиков, но и пользователей, менеджеров, а сам процесс разработки, как правило, происходит итерационно, итерационными улучшениями, постепенным переходом от процедурных знаний (как делать) - к непроцедурным (что делать).
Тестовые задания для самоконтроля
1) - предел деления системы с точек зрения решения конкретной задачи и поставленной
цели. Простейшая неделимая часть системы.
A) Элемент
Б) Подсистема
B) Структура Г) Связь
Д) Состояние
2) Возможность деления системы на связана с вычленением совокупностей
взаимосвязанных элементов, способных выполнять относительно независимые функции, подцели, направленные на достижение общей цели системы.
A) Элементы Б) Подсистемы
B) Структуры Г) Связи
Д) Состояния
3) - это совокупность элементов и связей между ними.
A) Элемент
Б) Подсистема
B) Структура Г) Связь
Д) Состояние
4) Понятие " " входит в любое определение системы наряду с понятием "элемент" и
обеспечивает возникновение и сохранение структуры и целостных свойств системы. Это понятие характеризует одновременно и строение (статику), и функционирование (динамику) системы.
А) Элемент Б) Подсистема
В)Структура Г) Связь Д) Состояние
5) Понятием " " обычно характеризуют мгновенную фотографию, "срез" системы,
остановку в ее развитии. Его определяют либо через входные воздействия и выходные сигналы (результаты), либо через макропараметры, макросвойства системы (например, давление, скорость, ускорение - для физических систем производительность, себестоимость продукции, прибыль - для экономических систем).
A) Элемент
Б) Подсистема
B) Структура Г) Связь
Д) Состояние
6) Если система способна переходить из одного состояния в друтое (например, Zi—»z2—»z3), то говорят, что она обладает
A) Поведением
Б) Устойчивостью
B) Равновесием Г) Развитием Д) целью
7) - это способность системы в отсутствие внешних возмущающих воздействий (или
при постоянных воздействиях) сохранить свое состояние сколь утодно долго.
A) Поведение Б) Устойчивость
B) Равновесие Г) Развитие Д) Цель
8) Под понимается способность системы возвращаться в состояние равновесия после
того, как она была из этого состояния выведена под влиянием внешних возмущающих воздействий. Эта способность обычно присуща системам при постоянном и„ если только отклонения не превышают некоторого предела.
A) Поведением
Б) Устойчивостью
B) Равновесием Г) Развитием Д) целью
9) Понятие помогает объяснить сложные термодинамические и информационные
процессы в природе и обществе.
A) Поведения Б) Устойчивости
B) Равновесия Г) Развития Д) Цели
10) - это идеальное устремление, которое позволяет коллективу увидеть перспективы
или реальные возможности, обеспечивающие своевременность завершения очередного этапа на пути к идеальным устремлениям.
А) Поведение Б) Устойчивость
В) Равновесие Г) Развитие
Д) Цель
11) Под системы понимается описание системы, отображающее определенную группу
ее свойств.
A) структурой Б) Моделью
B) Атрибутом Г) Функцией Д) Подсистемой
12) Это системы, основанные на знаниях (Knowledge Based System) - поддерживают задачи принятия решения в сложных системах, где необходимо использование знаний в достаточно широком диапазоне, особенно в плохо формализуемых и плохо структурируемых системах
A) экспертные системы
Б) интеллектуальные системы
B) математические системы Г) информационные системы Д) физические системы
Модуль 2. Информационные процессы - основа информационных систем
Тема 1. Понятие и структура информационного процесса
Математические модели сигнала.
Частотная форма представления детерминированных сигналов.
Классификация методов дискретизации.
Дискретизация по времени.
Выбор точности отсчетов по теореме Котельникова.
Квантование по уровню.
Лекция 7. Классификация методов дискретизации
Информация передается, и храниться в виде сообщений. Под сообщением понимают совокупность знаков или первичных сигналов содержащих информацию. Иначе говоря, сообщение - это информация представленная в какой-либо форме. Пример сообщений: текст телеграммы, данные на выходе ЭВМ, речь, музыка и т.д. Для того чтобы сообщение можно было передать получателю, необходимо воспользоваться некоторым физическим процессом, способным с той или иной скоростью распространяться от источника к получателю сообщения. Изменяющийся во времени физический процесс, отражающий передаваемое ообщение называется сигналом.
Сообщения могут быть функциями времени (когда информация представлена в виде первичных сигналов: речь, музыка) и не является ими (когда информация представлена в виде совокупности знаков).
Сигнал всегда является функцией времени. В зависимости от того, какие значения могут принимать аргумент (время t) и уровни сигналов их делят на 4 типа.
1) Непрерывный или аналоговый сигналы (случайные сигналы этого типа называются непрерывными случайными процессами). Они определены для всех моментов времени и могут принимать все значения из заданного диапазона.Чаще всего физические процессы, порождающие сигналы являются непрерывными. Этим и объясняется второе название сигналов данного типа аналоговый т.е. аналогичные порождающим процессам.
| 3)Дис назыв в реме] велич] |
| 4)Дис] дискр< разper |
рисунок 0.1
2) Дискретизированный или дискретно непрерывные сигналы (случайные сигналы этого типа называют процессами с дискретным временем или непрерывными случайными последовательностями). Они определены лишь в отдельные моменты времени и могут принимать любые значения уровня. Временной интервал Dt между соседними отсчетами называется шагом дискретизации. Часто такие сигналы называют дискретными по времени.
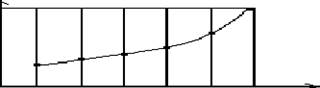 О Лг 2Лг Ar:J\x
О Лг 2Лг Ar:J\x
|
рисунок О
:ые сигналы этого типа лены для всех моментов деленные от друг друга на
I
рисунок О_3
гналы этого типа называют делены лишь в отдельные лпенные значения уровней.

|
рисунок 0.4-
| Канал | ||
| Передатчик |
| Принятый сигнал |
| Источник шума |
| Приемник |
| Принятое сообщение |
| Сообщение |
| Сигнал |
| Получатель сообщений |
| Источник сообщений |
Рисунок 0.5
Совокупность технических средств используемых для передачи сообщений от источника к потребителю информации называется системой связи. Общая схема системы связи представлена на рисунке 0.5.
Она состоит из 5 частей:
1) Источник сообщений создающий сообщения или последовательность сообщений, которые должны быть переданы. Сообщения могут быть разных типов: последовательность букв или цифр как в системах телеграфа и передачи данных. Одна или более функций времени как в системах передачи звука в моно и стерео звучаниях и т.д.
2) Передатчик, который перерабатывает некоторым образом сообщения в сигналы соответственного типа определенного характеристиками используемого канала.
3) Канал - это комплекс технических средств, обеспечивающий передачу сигналов от передатчика к приемнику. В состав канала входит каналообразующая аппаратура, осуществляющая сопряжение выходного и входного сигналов соответственно передатчика и приемника с линией связи, и самой линии связи. Линией связи называется среда, используемая для передачи сигнала от передатчика к приемнику. Это может быть, например: пара поводов, коаксиальный кабель, область распространения радиоволн, световод и т.д. Обычно входными и выходными сигналами линии связи является сигналы типа один, т.е. непрерывный. Вместе с тем на входе и выходе канала могут присутствовать сигналы и друтих типов. Канал называется дискретным, если на его входе и выходе присутствуют сигналы дискретные по уровню (сигналы типа 3,4). Если сигналы на входе и выходе канала непрерывны по времени (типа 1 или 2) то он называется непрерывным. В общем случае в процессе передачи в канале сигнал искажается шумом, что соответствует наличию рисунок 0.5 источника шума.
4) Приемник обычно выполняет операцию обратную по отношению к операции, производимой передатчиком, т.е. восстанавливается сообщение по сигналам. Сложность построения приемника обусловлена изменением формы принимаемых сигналов, что связано с наличием шума.
5) Получатель это лицо или аппарат, для которого предназначено сообщение. Процесс преобразования сообщения в сигнал, осуществляющий в передатчике и обратный ему процесс, реализующий в приемнике назовем соответственно кодированием и декодированием.
Тогда крут проблем составляющих основное содержание ТИ можно охарактеризовать как исследование методов кодирования для экономического представления сообщений различных источников сообщений и для надежной передачи сообщений по каналам связи с шумом.
В основе ТИ лежит статистическое описание источников сообщений и каналов связи, а так же базирующееся на этом описании измерении количества информации между сообщениями определенного только вероятностными свойствами сообщений и не от каких друтих их свойств независящих.
На основе ТИ можно ответить на вопросы о предельных возможностях (т.е. о
максимально достижимых характеристиках) различных систем, определить в какой мере проектируемая система уступает теоретически возможной. В некоторых случаях логика рассуждений, используемая в ТИ, подсказывает путь, на котором может быть найдено конструктивное решение для реальной системы.
Датой рождения ТИ 1948г. Год появления основополагающей статьи Клода Шеннона "Математическая теория связи". Начиная с этого времени, ТИ интенсивно развивалась в немалой степени благодаря работам и наших соотечественников Холмогорова, Добрушина, Хоркевича, Ханчина и друтих.
7.1 Получение дискретной модели сигнала
В любую систему информация поступает в виде сигналов. Различные параметры физических процессов с помощью датчиков обычно преобразуются в электрические сигналы. Как правило, ими являются непрерывно изменяющиеся ток или напряжение, но возможно поступление и импульсных сигналов, как, например, в радиолокации. Любая непрерывная (аналоговая) информация содержит бесконечное множество точек, что не может быть наблюдаемым с помощью реально существующей аппаратуры. Поэтому, а также в силу конечной чувствительности аппаратуры и ее разрешающей способности, любой аналоговый сигнал при его наблюдении представляется как ступенчатый. Так как ступенчатый сигнал в общем случае является неконтролируемым, необходима такая его модель, которая позволила бы оценить все его характеристики и в первую очередь - точность воспроизведения. Для получения модели ступенчатого сигнала используют квантование сигнала по уровню. Существует несколько способов такого квантования. Рассмотрим один из них. Для этого воспользуемся рисунком 2, где A(t) - непрерывный сигнал, AKB(t) - сигнал, полученный в процессе квантования. Сначала ось OA делят на отрезки равной длины (иногда разной). Через концы отрезков проводят линии параллельно оси времени. Полученные линии называются уровнями квантования и обозначаются Ai, где i - номер уровня. АО - А5 - значения уровней квантования. Находим середины между уровней (пунктирные линии). ДА1 - шаг квантования по уровню. Находим точки пересечения пунктирной линии с A(t). Значения функций, принадлежащих ДА1> заменяем значением уровня.
 Рисунок 2. Квантование по уровню
Рисунок 2. Квантование по уровню
|
Квантованная функция AKB(t) получается заменой значений функции A(t) значениями Ai-x уровней в каждом Ai-м шаге. При таком квантовании в силу случайной функции A(t) моменты времени tl, t2,... переходов с уровня на уровень являются случайными, т.е. функция AKB{t) отличается от функции A(t) тем, что содержит конечное число значений по
амплитуде, равное числу уровней квантования. Точность квантования по уровню определяется величиной шага квантования по уровню ДА. Чем меньше значение ДА, тем точнее модель квантованного по уровню сигнала.
lirri A j) = A(t)
ЛА-*0 К F (1)
Сигнал, квантованный по уровню, обладает большей помехозащищенностью по сравнению с неквантованным, т.к. при передаче по каналу значения уровня (или его номера) помехи не переводят этот уровень в друтой, например соседний, если амплитуда помехи не превышает половины шага квантования. Критерии точности и помехозащищенности взаимно противоречивы. Для повышения точности необходимо уменьшить шаг квантования по уровню, а для повышения помехоустойчивости сигнала шаг квантования надо увеличить. Поэтому задача квантования по уровню является минимаксной и решается так, чтобы при заданной точности обеспечить минимальное воздействие помех или при заданной помехозащищенности обеспечить максимальную точность.
Второй способ квантования - квантование сигнала по времени позволяет получить дискретную модель сигнала, которая с точки зрения модуляции может использовать только амплитудоимпульсную модуляцию (рисунок 3).
 Рисунок 3. Квантование по времени
Рисунок 3. Квантование по времени
|
Модель сигнала при квантовании по времени характеризуется тем, что, несмотря на бесконечно большое число различных значений амплитуд сигнала, которые берутся в моменты времени, кратные шагу квантования по времени ДТ, т.е. число передаваемых значений сигнала конечно. Каждое такое значение называют отсчетом или дискретом. Для обеспечения нужной точности передачи информации следует шаг квантования по времени
выбрать малым.
При квантовании по времени главным является вопрос о количестве дискретов информационно-составляющих исходной аналоговой функции A(t), описывающей сигнал. С практической точки зрения количество дискретов желательно иметь минимально возможным, т.е. желательно иметь как можно больший шаг квантования ДТ. Но при этом уменьшается точность воспроизведения информации. При квантовании по времени должен быть использован некоторый критерий точности преобразования сигнала. Чаще всего - это критерий минимума среднеквадратической ошибки. В первые математическую основу такого преобразования информации дал В.А. Котельников, сформулировавший следующую теорему:
Если непрерывная функция A(t) в своем частотном спектре не содержит частот выше некоторой частоты Fm, то такая функция может быть полностью представлена своими дискретными значениями, взятыми с интервалом ДТ, если выполняется условие: 1
AT
2 F
(2)
fc-i -ьат) ^
- 2
где т,Гг.
Ряд Котельникова позволяет восстановить аналоговую функцию A(t), используя алгоритм, основанный на работе генераторов отсчетов (фильтров отсчетов). Каждый такой генератор воспринимает свой отсчет и формирует свою синусоидальную составляющую ряда как отклик на полученный отчет. Сумма таких откликов дает возможность получить исходную функцию A(t). Важным фактором является то, что в качестве генераторов отсчетов можно иметь число генераторов меньше числа отсчетов, если реализовать алгоритм восстановления функции A(t) на основе фильтров отсчета с запаздыванием и памятью.
Рассмотрение энергетического спектра сигналов с ограниченной полосой частот ("^ - верхняя частота полосы пропускания) дает возможность оценить погрешность преобразования Котельникова (рисунок 4). Очевидно, эту погрешность можно косвенно
оценить через энергию, заключенную в сигнале до частоты Если считать, что как показывает рассмотрение стандартных спектров наиболее употребительных дискретных
сигналов, что в диапазоне частот от 0 до "^содержится не менее 98% полной энергии сигнала, то погрешность преобразования Котельникова не должна превышать 5%. Если задана некоторая требуемая точность преобразования, то в общем случае относительная погрешность такого преобразования д может быть определена по формуле:
" Е > (4)
где д - допустимая погрешность, Е - полная энергия сигнала, ДЕ - неучитываемая энергия (энергия сигнала за
 Рисунок 4. Энергетический (частотный) спектр, ограниченный частотой
Рисунок 4. Энергетический (частотный) спектр, ограниченный частотой
|
Если учесть, что все реальные системы имеют ограниченный частотой "^спектр, и одновременно ограничены по времени, то преобразование аналогового сигнала в дискретный по теореме Котельникова корректно и точность этого преобразования всегда может быть оценена через среднеквадратическую ошибку, которая тем меньше, чем меньше шаг дискретизации ДТ. Теоретически при ДТ 0 ошибка становится нулевой, но, оставаясь в дискретной области, всегда можно обеспечить сколь угодно малую ошибку преобразования Котельникова. В теории информации в разделе «Теория сигналов» вводится понятие базы сигнала или число степеней свободы сигнала. База сигнала тем больше, чем больше произведение длительности сигнала на ширину полосы пропускания. Имея ввиду базу сигнала, можно из формулы Котельникова получить, что
Третий способ квантования - квантование по уровню и по времени (рисунок 5). При квантовании обоих видов алгоритмически сначала информация квантуется по уровню, т.е. ограничивается по числу возможных для использования значений амплитуд сигналов. В качестве второго алгоритмического шага обработки информации используют квантование по времени. При этом ограничивается число отсчетов (дискретов), но каждый отсчет (дискрет) при этом имеет амплитуду, равную амплитуде какого-либо уровня квантования, т.е. в отличие от сигналов, квантованных только по уровню или по времени, в данном случае сигнал ограничен и по числу возможных амплитудных значений, и по количеству этих значений.
Рисунок 5. Квантование по уровню и по времени
Если проанализировать информацию в виде дискретов, заданных уровневых значений, то для характеристики такой информации можно от реальных значений амплитуд уровней перейти к номерам уровней. Что может ввести в рассмотрение некоторый код для передачи номеров уровней, а так, как число уровней всегда известно (пусть оно равно N), то всегда будет определено число разрядов кода (п).
> lag л Л^
необходимое для передачи N уровней. Здесь а - основание кода. Так как при работе в системах передачи информации передача предыдущих дискретов должна заканчиваться до начала передачи последующих дискретов, то, если известна длительность передачи каждого из п - разрядов кода, должно выполняться условие:
где t„ - длительность передачи каждого из п разрядов. Построенный по такому принципу сигнал, и информация, передаваемая им, называются цифровыми, т.е. цифровой сигнал - это сигнал, квантованный и по уровню, и по времени.
Перейдем к рассмотрению наиболее полной универеальной структурной схеме, в которой САУ работает в имитируемой на СПМ внешней среде (рисунок 6). Определение: Стенд полунатурного моделирования - система, осуществляющая имитацию внешней среды и всех взаимодействующих в САУ устройств. Он предназначен для проведения отладки САУ с минимальным (и только на конечном этапе отработки) применением дорогостоящих полнонатурных испытаний.
Тестовые задания для самоконтроля
1) По какой теореме рассматривается равномерная дискретизация по частотному критерию
A) Котельникова Б)Шеннона
B) Файра
2) позволяет получить дискретную модель сигнала, которая с точки зрения модуляции
может использовать только амплитудоимпульсную модуляцию
А) квантование сигнала по времени Б) квантование сигнала по уровню
В) квантование сигнала по уровню и по времени Г) квантование сигнала в определенный момент времени Д) нет правильных ответов
3) алгоритмически сначала информация квантуется по уровню, т.е. ограничивается по
числу возможных для использования значений амплитуд сигналов.
A) квантование сигнала по времени Б) квантование сигнала по уровню
B) квантование сигнала по уровню и по времени
Г) квантование сигнала в определенный момент времени Д) нет правильных ответов
4) обладает большей помехозащищенностью по сравнению с неквантованным, т.к. при
передаче по каналу значения уровня {или его номера) помехи не переводят этот уровень в
друтой, например соседний, если амплитуда помехи не превышает половины шага квантования.
A) квантование сигнала по времени Б) квантование сигнала по уровню
B) квантование сигнала по уровню и по времени
Г) квантование сигнала в определенный момент времени Д) нет правильных ответов
Тема2. Модели процесса передачи
Измерение информации. Модель непрерывного и дискретного каналов связи. Пропускная способность дискретного и непрерывного каналов связи. Оценка потерь информации. Понятие избыточности информации.
ИНФОРМАЦИИ ТЕОРИЯ - раздел математики, исследующий процессы хранения, преобразования и передачи информации. В основе его лежит определенный способ измерения количества информации. Возникшая из задач теории связи, теория информации иногда рассматривается как математическая теория систем передачи информации. Опираясь на основополагающую работу К.Шеннона (1948), теория информации устанавливает основные границы возможностей систем передачи информации, задает исходные принципы их разработки и практического воплощения. В настоящей статье рассматривается ядро теории информации - свойства информационных мер и их приложения к анализу систем передачи информации.
Основные свойства информации можно описать с помощью математической модели, отражающей многие характерные особенности информационной меры, как она обычно понимается на интуитивном уровне. Источник информации и канал связи, по которому передается информация, можно моделировать, используя вероятностные представления. Энтропия источника информации равна логарифму (эффективного) числа сообщений, которые он порождает. Это - мера сложности описания источника (или, как иногда говорят, мера неопределенности сообщения). Такое понимание энтропии тесно связано с понятием энтропии, используемым в термодинамике (ем, т акже ТЕРМОДИНАМИКА). Физически передачу информации можно представить как индуцирование в приемном устройстве требуемого физического состояния. Отправитель намерен передать сообщение получателю. Суть передачи заключается в воспроизведении на выходе канала связи переданного сообщения. В момент передачи отправитель выбирает нужное сообщение из списка всех возможных сообщений. Получатель заранее не знает, какое из них будет выбрано. (Если бы он был об этом заранее информирован, то никакой необходимости посылать сообщение не было бы.) Канал связи вносит в процесс передачи информации случайный шум, который искажает сообщение и тем самым затрудняет его прочтение. В начале процесса связи получатель находится в полной неопределенности относительно того, какое сообщение выбрано из списка возможных. К концу связи получателю становится это известно, т.е. становится известно точное описание выбранного сообщения. Способность канала связи передавать информацию характеризуется некоторым числом - пропускной способностью (емкостью), равной логарифму эффективного числа сообщений, различимых на его выходе. Процесс передачи информации можно считать надежным, если скорость передачи сообщений меньше пропускной способности канала. В противном случае надежная передача информации оказывается невозможной. Основной результат теории информации состоит в утверждении: если энтропия источника меньше пропускной способности канала, то на его выходе исходное сообщение может быть воспроизведено со сколь утодно малой ошибкой; если же энтропия источника превышает его пропускную способность, то ошибку сделать малой невозможно.
Трудность передачи сообщения не зависит от его содержания; передавать бессмысленные сообщения не менее трудно, чем осмысленные. Например, число 23 в одном контексте может быть ценой одного барреля нефти, а в друтом - номером победителя заезда на скачках. Смысл сообщения зависит от контекста и семантики, а трудность его передачи определяется только перечнем возможных сообщений (и их вероятностей). Любую систему передачи информации можно считать состоящей из трех частей: источника сообщений, канала связи и приемного устройства (рис. 1). Например, при разговоре по телефону источником является говорящий, сообщением - его речь. Каналом связи служат провода, передающие электрический сигнал от говорящего к слушателю - получателю сообщения.
Между отправителем сообщения и каналом связи могут находиться устройства (обозначенные на рис. 1 как кодирующие), преобразующие сообщение в форму, удобную для передачи по каналу связи. Декодирующее устройство, установленное на друтом конце канала, восстанавливает принятое сообщение.

|
Изучение систем передачи информации мы начнем с источника сообщений. По каналу связи может передаваться самая различная информация: текст, живая речь, музыка или изображения. Для каждого источника можно указать перечень сообщений, которые он может генерировать. Например, источник телеграфных или телексных сообщений передает только буквы и не содержит, скажем, нотных знаков. Если по каналу связи передается живая речь, то сигнал лишается полезного содержания при частоте выше 20 ООО Гц, верхнего предела, воспринимаемого человеческим слухом. Этими фактами можно воспользоваться при проектировании входа канала связи.
Не нашли, что искали? Воспользуйтесь поиском: