ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Расчет балок на прочность по нормальным напряжениям
При расположении мостов на прямых участках пути основными нагрузками, учитываемыми при расчете грузоподъемности, являются временная вертикальная нагрузка от подвижного состава и постоянная от собственного веса пролетного строения.
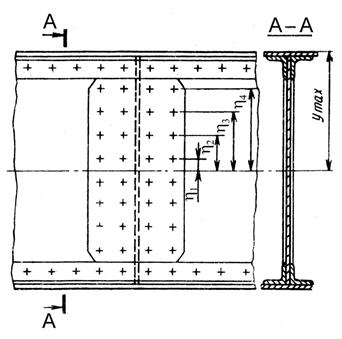
Условие прочности изгибаемых балок пролетного строения рассматривается по нормальным напряжениям в сечениях, где происходит изменение геометрического факторов сечения. В этой связи расчет балок на прочность по нормальным напряжениям производится для сечений: в середине пролета, в местах обрывов горизонтальных листов поясов (по первому ряду заклепок), в стыках поясов и стенок балки, в местах с наибольшими ослаблениями (коррозией и другими), а также других опасных сечениях (рис. 1)
|
Условие предельного состояния при расчете на прочность главных балок по нормальным напряжениям:
σ =  , (8)
, (8)
где Мр – расчетный изгибающий момент от постоянных нагрузок
Мр = εрР 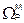 ; (9)
; (9)
Мk – то же от временной классифицируемой допускаемой нагрузки
Мk = εknkknн 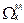 ; (10)
; (10)
где εk, εр – доля вертикальной временной от подвижного состава и постоянной нагрузки, приходящиеся на одну балку.
При совпадении оси пути с осью однопутного пролетного строения коэффициенты εk = εр = 0.5.
При несовпадении оси пути с осью пролетного строения коэффициент εk определяется:
εk = 0.5 + lср/b, (11)
где lср – среднее смещение оси пути относительно оси пролетного строения; b – расстояние между осями главных балок.
В отдельных случаях при наличии односторонних обустройств (специальных пешеходных тротуаров, кабельных мостиков, трубопроводов и др.), перегружающих одну из балок, коэффициент εр определяется:
εр = 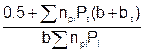 , (12)
, (12)
где npi – коэффициент надежности к постоянным нагрузкам: при определении веса металла пролетного строения на основании ведомости исчисления веса металла – 1.05 или 0.95; при определении веса металла пролетного строения по графикам приложения 1, а также при определении веса смотровых приспособлений, коммуникаций (трубопроводов, кабелей) и других обустройств, расположенных на пролетном строении, кроме веса мостового полотна – 1.1 или 0.9. Значение np больше или меньше единицы принимается в зависимости от того, какое из них повышает абсолютную величину суммарного воздействия; Pt – интенсивность постоянных нагрузок от веса односторонних обустройств; bt – расстояние от оси перегруженной балки до равнодействующей постоянных нагрузок от веса односторонних обустройств; Pi – интенсивность симметричных постоянных нагрузок (вес металла пролетного строения, мостового полотна и др.);
nk – коэффициент надежности к вертикальной нагрузке от подвижного состава, который принимается равным:
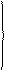 |
λ = 0 nk = 1.15;
λ = 50 м nk = 1.10; (13)
λ = 150 м nk = 1.05,
где λ – длина загружения линии влияния, промежуточные значения nk принимаются по интерполяции;
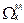 ,
, 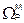 - площади линии влияния изгибающего момента, загружаемые нагрузкой от подвижного состава или постоянной нагрузкой (см. рис.1):
- площади линии влияния изгибающего момента, загружаемые нагрузкой от подвижного состава или постоянной нагрузкой (см. рис.1):
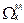 =
= 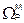 = α(1-α)lp2/2; (14)
= α(1-α)lp2/2; (14)
р – суммарная расчетная интенсивность постоянных нагрузок:
р = np1Pпс + n р2P м.п. , (15)
где Pпс – вес металла однопутных балочных разрезных пролетных строений, определяемый по графикам приложения 1; Pм.п. – вес мостового полотна, определяемый по табл. приложения 1.; np1 = 1.1 и np2 = 1.2 – коэффициенты надежности к постоянным нагрузкам;
с – коэффициент, учитывающий ограниченное развитие пластических деформаций в сечении при проверке его на изгиб: для балок со сплошной стенкой при расчете на прочность с = 1.1; на выносливость с = 1.0;
W0 – расчетный момент сопротивления поперечного сечения балки, который при расчете по сечению, проходящему вне пределов стыка, равен моменту сопротивления нетто поперечного сечения балки Wнт:
W0 = Wнт = Iнт / ymax, (16)
где Iнт – момент инерции нетто поперечного сечения балки относительно нейтральной оси; ymax – расстояние от нейтральной оси до наиболее удаленного волокна рассматриваемого сечения (рис.2).
|
Рис. 2 Схема для расчета балки в зоне стыка:
η 1, η2 – расстояния от нейтральной оси до центра ближайшего ряда заклепок; ymax – то же до наиболее удаленного волокна.
Для клепаных балок без горизонтальных поясных листов разрешается принимать Wнт = 0.82Wбр , а для балок с горизонтальными листами Wнт = 0.8Wбр , где Wбр – момент сопротивления поперечного сечения брутто. Ослабление стенки допускается принимать равным 15%.
При расчете по сечениям, расположенным в пределах стыка, за рабочий момент сопротивления балки принимается (см. рис.2)
W0 =  , (17)
, (17)
где åIц – сумма моментов инерции нетто поперечного сечения частей, не имеющих стыков или обрывов в рассматриваемом сечении, относительно нейтральной оси всего сечения балки; åIсц – сумма моментов инерции нетто относительно той же нейтральной оси балки поперечного сечения накладок (åIнц) или приведенной площади заклепок (болтов), прикрепляющих накладки (åni2/m0); 1/m0 – приведенная площадь заклепки (болта), по данным приложения 2; hi – расстояние от нейтральной оси балки до i-й заклепки (болта). Для горизонтальных заклепок (болтов) hi принимается до оси отверстия, а для вертикальных – до соответствующей плоскости среза. В сумму åIсц подставляется меньшее из значений åIнц или åni2/m0.
Значение m0 для заклепок определяется в зависимости от характера их работы. С учетом того, что на единицу (см2, м2) рабочей площади поперечного сечения элемента можно допустить усилие, равное R, число заклепок, необходимое для прикрепления единицы рабочей площади элемента, определится:
по одиночному срезу
n = 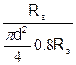 = m0cp; (18)
= m0cp; (18)
по смятию металла
n =  = m0cм. (19)
= m0cм. (19)
При одинаковых основных сопротивлениях металла элемента и заклепки (см. приложение 2):
m0cp = 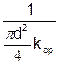 ; (20)
; (20)
m0cм = 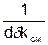 , (21)
, (21)
где d – диаметр заклепки; d - толщина элемента, наиболее слабого по смятию; Rз и Rэ – расчетное сопротивление металла заклепки и элемента.
Значение mб для высокопрочных болтов по одному контакту трения определяется аналогично предыдущему (см. прилож. 2):
mб = 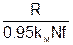 , (22)
, (22)
где N – нормативное натяжение болта, f – коэффициент трения по контактирующим поверхностям.
В случае сварного стыка значение åIсц заменяется значением момента инерции относительно нейтральной оси балки расчетных площадей сварных швов, определяемых согласно приложения 3.
Окончательно условие прочности изгибаемой балки пролетного строения по нормальным напряжениям примет вид:
s = 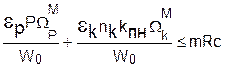 , (23)
, (23)
где m – коэффициент условий работы, равный 1.0; R – основное расчетное сопротивление металла. Для элементов, работающих на изгиб, растяжение и сжатие значения R приведены в табл. 3
Таблица 3
Основные расчетные сопротивления
| Металл | R, Мпа (кг/см2) |
| Сварочное железо (в том числе заклепки) | 160 (1600) |
| Литое железо выплавки до 1906 г. (в том числе заклепки); | 185 (1850) |
| Литое железо выплавки после 1906 г. (в том числе заклепки), стали марок: Ст3; Ст3 мост.; М16С НЛ2 | 190 (1900) 260 (2600) |
| Стальное литье, в том числе и неизвестных марок | 170 (1700) |
| Стали марок: Ст5 в катках и болтах-шарнирах Ст2 (для заклепок) 09Г2 (для заклепок и болтов) 40Х (для высокопрочных болтов) | 200 (2000) 190 (1900) 240 (2400) 770 (7700) |
| Чугун, в том числе и неизвестных марок, на растяжение при изгибе | 55 (550) |
Примечания: 1. Расчетные сопротивления включают в себя общий коэффициент условий работы m=0.9, учитывающий несоответствие фактических механических свойств металла конкретного пролетного строения принятым при назначении расчетного сопротивления; неточности при определении величины повреждений металла коррозией; отступления принимаемых в расчетах размеров сечений от фактических за счет допусков и др. [2]. Для мостовых сталей, не указанных в таблице, основное расчетное сопротивление принимается по действующим нормам проектирования железнодорожных мостов [3]. Если марка стали неизвестна, то основное расчетное сопротивление принимается по результатам испытания образцов, меньшим из двух значений: 80% предела текучести или 50% предела прочности.
Учитывая выражение (23), допускаемая временная вертикальная нагрузка из расчета на прочность по нормальным напряжениям kпн определится:
kпн =  . (24)
. (24)
Допускаемая временная нагрузка по выражению (24) определяется для всех проверяемых сечений балки (см. рис. 1).
Класс балки пролетного строения определяется по формуле (1).
Не нашли, что искали? Воспользуйтесь поиском: