Общее условие устойчивости линейных систем.

Основные понятия и определения.

Важнейшим из свойств процессов, протекающих в системах автоматики, является устойчивость - это основное качественное свойство, без которого система не работоспособна. Физически устойчивость означает, что при ограниченном входном сигнале выходной сигнал также является ограниченным и процессы в системе стремятся к определенному значению при любых начальных условиях. Для линейной системы устойчивость определяется только ее структурой и параметрами и не зависит от величины внешних воздействий и начальных условий. Очевидно, что для переходной характеристики устойчивой системы справедливо условие

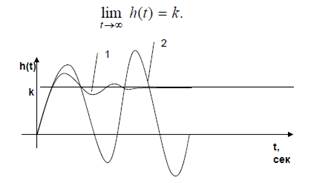
Переходные характеристики системы:

1 – сходящийся процесс, система устойчива; 2 – расходящийся процесс, система неустойчива

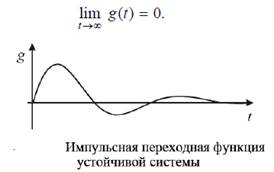
Об устойчивости можно судить также по импульсным переходным функциям, которые в случае устойчивой системы удовлетворяют условию

Рассмотрим, как можно оценить это свойство для систем, поведение которых описывают уравнения

Определим зависимость переменных состояния от времени как решение векторно-матричного уравнения состояния в виде

Здесь первое слагаемое соответствует свободной составляющей движения (из произвольных начальных условий), второе – вынужденной (движение под действием управления). Одним из основных режимов работы системы управления является равновесный (статический) режим, при котором переменные состояния с течением времени не меняются, а все производные координат состояния равны нулю. Покажем, что процесс движения к равновесию можно считать свободным, т. е. он соответствует первому слагаемому в выражении (4.2). Предварительно запишем уравнение статики, полагая в (6.1)

откуда при det A≠0 определим равновесное значение переменных состояния

Введем новые координаты, равные отклонениям от точки равновесия,

и запишем для них дифференциальное уравнение

так как x⁰=0.

После подстановки в (4.6) вместо его значения из (4.1) с учетом (4.5) получим

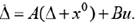
Учитывая (4.4), уравнение в отклонениях принимает вид

Как видим, уравнение (4.7) не содержит u, и поэтому переходный процесс по Δ порождается только ненулевыми начальными условиями согласно уравнению

Линейная система (4.1) называется устойчивой, если для ее процессов выполняется условие

Оно представляет собой предел выражения (4.8), которое соответствует первой составляющей решения (4.2). Таким образом, устойчивость линейной системы (4.1) определяется только ее структурой и параметрами и не зависит от величины внешних воздействий и начальных условий. Причем для анализа устойчивости можно не переходить к уравнениям в отклонениях от состояния равновесия, а исследовать свойства матрицы A.

Общее условие устойчивости линейных систем.

Для устойчивости линейной системы (4.1) необходимо и достаточно, чтобы вещественная часть всех собственных значений матрицы A (корней характеристического уравнения) была отрицательной, т. е.

Покажем справедливость этого утверждения, для чего запишем характеристическое уравнение системы (4.1)

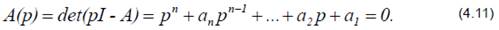
и найдем его корни . Используя модальное представление, определим полный процесс в системе, который представляет собой сумму экспонент

Как видим, качественный характер переходных процессов полностью определяется значениями корней. В случае, когда все они вещественные и отрицательные, каждая компонента выражения (4.12) при выполнении условия (4.10) носит затухающий характер. Следовательно, и их сумма также будет иметь затухающий характер, т. е. будет с течением времени стремиться к нулю.

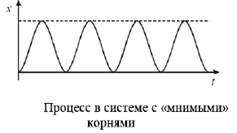
Если корни характеристического уравнения (4.11) комплексно-сопряженные с отрицательной вещественной частью, то каждая пара их дает колебательную составляющую процесса, которая мажорируется затухающей экспонентой.

Следовательно, и в этом случае процесс, определяемый соотношением (4.12), будет иметь затухающий характер. Это достаточность условия устойчивости (4.10).

Покажем теперь необходимость этого условия. Предположим, что, хотя бы один из корней имеет положительную вещественную часть. Соответствующая ему составляющая решения будет с течением времени возрастать и в пределе стремиться к бесконечности.

Следовательно, полный процесс, который определяется выражением (4.12), будет иметь расходящийся характер,

а система (4.1) никогда не сможет стать устойчивой. Изобразим корневой портрет системы и получим графическую интерпретацию условия (4.10): для устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического уравнения располагались в левой полуплоскости плоскости корней Корневой портрет системы Если, хотя бы один корень находится в правой полуплоскости плоскости корней, то система будет неустойчива. Мнимая ось представляет собой границу устойчивости системы:

Не нашли, что искали? Воспользуйтесь поиском: