
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Алгебраические и частотные критерии устойчивости.
Критерий Гурвица
Этот критерий сформулирован математиком А. Гурвицем в 1895 г., он является алгебраическим и связывает расположение корней характеристического уравнения с определенными условиями, которые накладываются на его коэффициенты.
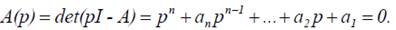
по следующему правилу составляется матрица Гурвица: на главной диагонали сверху вниз выписываются по порядку коэффициенты характеристического уравнения от до включительно. В каждом столбце вниз от диагонали записывают коэффициенты при возрастающих степенях оператора p, вверх – при убывающих степенях p. Недостающие элементы в столбце дополняются нулями.
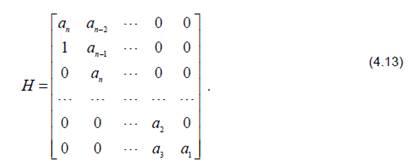
Формулировка критерия. Для устойчивости линейной системы необходимо и достаточно, чтобы все n диагональных миноров, полученных из матрицы Гурвица H, были положительны:

Здесь Δi– определители Гурвица, которые составляются следующим образом:

Поскольку определитель n-1 –го порядка должен быть положительным, последнее условие соответствует требованию a1>0.
Следствием критерия является условие границы устойчивости, когда последний определитель Гурвица обращается в нуль:
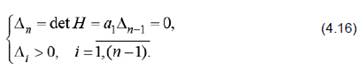
Критерий Михайлова
Критерий сформулирован математиком А.В. Михайловым в 1938 г. Он базируется на принципе аргумента теории функций комплексной переменной. Для анализа устойчивости системы предлагается исследовать характеристический комплекс F(jω), который получается из характеристического полинома:

заменой p на jω
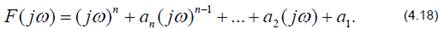
Выделим в (4.14) вещественную и мнимую части, а также модуль и фазу:

При конкретном численном значении частоты (ω=ω 1) характеристический комплекс (4.19) представляет собой комплексное числоF(j 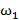 ) которое можно изобразить на плоскости в виде вектора, соединяющего начало координат с точкой RF(
) которое можно изобразить на плоскости в виде вектора, соединяющего начало координат с точкой RF(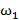 ), jIF(
), jIF(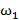 ).
).
При изменении ω от 0 до ∞ конец вектора F(jω)выписывает на
комплексной плоскости некоторую кривую, которую называют годографом Михайлова (см. рис.). Причем начинается годограф, как следует из соотношения (4.18), в точке с координатами a1, j0.
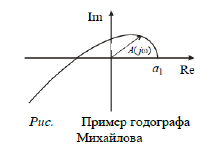
Формулировка критерия. Для устойчивости линейной системы необходимо и достаточно, чтобы годограф Михайлова при изменении от ω от 0 до ∞ начинался на вещественной оси в точке и проходил последовательно против часовой стрелки n квадрантов комплексной плоскости, не обращаясь в нуль и стремясь к в n-м квадранте в ∞. Пример годографов Михайлова для устойчивых и неустойчивых систем третьего порядка приведен на рис.
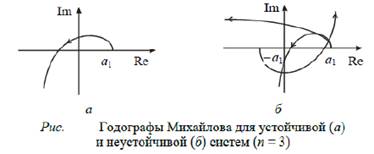
Условием границы устойчивости является обращение в нуль годографа Михайлова при некотором значении частоты ω = ω0. Аналитически это условие можно записать в виде:

Здесь ω0 – частота незатухающих колебаний, возникающих в системе, которая находится на границе устойчивости.
Критерий Найквиста
На практике более широкое применение по сравнению с критерием Михайлова получил критерий Н. Найквиста, который был разработан в 1932 г. для проверки устойчивости усилителей с отрицательной обратной связью, а затем обобщен на системы автоматического управления. Критерий Найквиста позволяет определить устойчивость системы с отрицательной обратной связью (так называемой замкнутой системы) по экспериментально снятой или полученной на основе передаточной функции амплитудно-фазовой частотной характеристики разомкнутой системы.

Рассмотрим этот критерий для системы с единичной обратной связью (рис). Здесь W0(p)– передаточная функция устойчивой разомкнутой системы, которая в общем случае имеет вид:

где ее характеристический полином 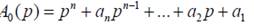 .
.
Определим передаточную функцию системы, изображенной на рис.
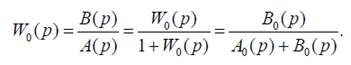
где 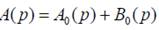 характеристический полином замкнутой системы.
характеристический полином замкнутой системы.
Формулировка критерия Найквиста: для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика устойчивой разомкнутой системы при изменении ω от 0 до ∞ не охватывала точку с координатами -1; j0.
Примеры расположения частотных характеристик, соответствующих устойчивой и неустойчивой замкнутым системам, приведены на рис.

Разомкнутая система может быть неустойчива, однако это не означает, что неустойчивой будет и замкнутая система. В этой ситуации следует использовать видоизмененную формулировку критерия Найквиста: замкнутая система будет устойчива тогда и только тогда, когда амплитудно-фазовая характеристика неустойчивой разомкнутой системы при изменении ω от 0 до ∞ охватывает точку с координатами -1; j0 в положительном направлении r/2 раз, где r– число корней характеристического уравнения разомкнутой системы с положительной вещественной частью.
Сформулируем теперь условие границы устойчивости. Замкнутая система будет находиться на границе устойчивости, если при некоторой частоте ω = ω0 амплитудно-фазовая характеристика разомкнутой системы проходит через точку с координатами -1; j0.
Аналитически это условие можно записать в виде:
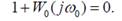
Пример расположения для этой ситуации амплитудно-фазовой характеристики разомкнутой системы на комплексной плоскости представлен на рис.

Предварительно необходимо получить передаточную функцию разомкнутой системы, для чего можно размыкать связь произвольным образом (рис.), а вход и выход системы следует рассматривать в месте разрыва. В результате искомая передаточная функция будет иметь вид:


Не нашли, что искали? Воспользуйтесь поиском: