Области и запасы устойчивости.

Основные понятия и определения

Поскольку математическая модель никогда не бывает тождественна физической системе, а при ее составлении делается ряд допущений, параметры реальной системы несколько отличаются от расчетных (номинальных). Кроме того, с течением времени параметры могут изменяться в некотором диапазоне, но для нормального функционирования системы свойство устойчивости должно сохраняться, т. е. она должна обладать определенным запасом устойчивости. Введем понятие запаса устойчивости для системы, модель которой имеет вид:

Запишем характеристическое уравнение системы

Оно имеет n корней

Определение: областью устойчивости по параметрам будем называть множество матриц A, для которых выполняется общее условие устойчивости линейных систем, т. е.

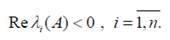
Совокупность всех этих матриц A отображается в некоторую область на плоскости параметров

Определение: критическими (граничными) будем называть такие значения матриц Aгр, при которых система находится на границе устойчивости.

В реальной ситуации часто требуется оценить влияние одного параметра системы (например, a) на ее устойчивость, поэтому можно говорить о «левом» и «правом» граничных значениях, например, a1гр и а2гр соответственно.

Определение: запасом устойчивости называется диапазон значений параметра от номинального до граничного. Например,

Частотные оценки запаса устойчивости

На основе критерия Найквиста можно получить частотные оценки

запаса устойчивости, которые характеризуют удаление амплитудно-фазовой характеристики разомкнутой системы от критической точки -1; j0. Запас устойчивости по модулю (h) показывает, насколько можно увеличить модуль АФХ разомкнутой системы без потери устойчивости замкнутой

Запас устойчивости по фазе ( γ ) определяется на частоте среза ωср, где . Он показывает, насколько можно изменить фазу АФХ разомкнутой системы без потери устойчивости замкнутой

Корневые оценки запаса устойчивости

Оценить запас устойчивости системы можно также по ее корневому портрету. На рис. ниже приведены графики переходных процессов двух систем. Видно, что система 2 обладает меньшим запасом устойчивости, поскольку склонность к неустойчивости выражается в большой колебательности процессов.

В свою очередь, характер процессов в системе определяется ее полюсами согласно выражению, причем колебания будут возникать, если характеристическое уравнение содержит комплексно-сопряженные корни:

где вещественная часть определяет скорость затухания, а

мнимая часть корней – частоту колебаний.

Паре корней с самым «широким» сектором (рис) будет соответствовать составляющая процесса с наибольшими колебаниями, поэтому в качестве оценки запаса устойчивости можно рассматривать отношение

Отметим, что значение γ может изменяться в диапазоне γ ∈0; ∞.

Чем меньше γ (больше величина мнимой части корня βi или меньше вещественная часть), тем ближе будет система к границе устойчивости. В случае, когда γ =0,

она находится на границе устойчивости. При γ = ∞ система будет иметь бесконечный запас устойчивости.

Таким образом, корневая оценка запаса устойчивости характеризует, насколько можно изменять корни характеристического уравнения без потери системой устойчивости.

Обычно такая оценка используется на этапе проектирования, так как ее трудно связать с параметрами реальной системы автоматического управления (коэффициентом усиления, постоянными времени, коэффициентом демпфирования).

Заключение: В этой главе мы рассмотрели понятие устойчивости линейных систем, которое является одним из важнейших ее качественных свойств и обусловливает работоспособность системы автоматического управления. Отметим, что устойчивость линейной системы определяется ее собственными свойствами и не зависит от внешних факторов, поэтому она будет предсказуемым образом реагировать на различные внешние воздействия и начальные условия.

Для анализа устойчивости в зависимости от ситуации можно использовать различные критерии, описание которых приведено в разделе.

С целью нормального функционирования системы свойство устойчивости должно сохраняться при изменении ее параметров в некотором диапазоне, поэтому на этапе проектирования необходимо проверять наличие определенного запаса устойчивости системы. Приведены также способы их оценки.

Не нашли, что искали? Воспользуйтесь поиском: