С использованием отклонений от скользящей средней

Перевод первоначальных данных в логарифмическую форму, предприня­тый на шаге 3, лишь частично удаляет тренд, и, как только что было пока­зано, остатки тренда в данных могут значительно повлиять на проверку статистической надежности. Отклонения от скользящей средней являют­ся наилучшим способом полностью снять направленность с данных. Откло­нения вычисляются путем вычитания скользящей средней данных из самих данных. Поскольку скользящая средняя отражает тренд в данных, вычи­тание ее из данных приводит к сериям, в которых нет тренда (рис. 16.11). Когда центрированная скользящая.средняя вычитается из первона­чальных данных, в результате получаются новые временные ряды, со­ставленные из отклонений или остатков от скользящей средней. Для каждого потенциального цикла, идентифицированного с помощью спек­трального анализа, будут выведены отдельные серии отклонений. Вы­числение серий отклонений проиллюстрировано на тех же данных, ко­торые ранее были использованы, чтобы показать процесс вычисления центрированной скользящей средней:

Начальные данные 134,500 141,20 132,40 138,90 Логарифмы данных 2,1287 2,1498 2,1219 2,1427

596 ЧАСТЬ 3. осцилляторы и циклы

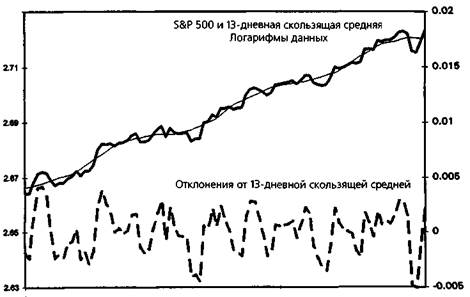
Рисунок 16.11. УДАЛЕНИЕ ТРЕНДА С ПОМОЩЬЮ ОТКЛОНЕНИЙ

Значение центрированной
скользящей средней 2,1335 2,1381

Отклонение (остаток) 0,0163 -0,0162

Метод отклонений от скользящей средней следует использовать очень осторожно из-за взаимодействия длины скользящей средней и периода данных (если они цикличны). Рис. 16.12 показывает, как выг­лядит скользящая средняя данных с безупречным 25-дневным циклом: скользящая средняя, рассчитанная по количеству точек, меньшему чем период цикла, будет содержать тот же цикл, но с меньшей амплитудой; скользящая средняя той же длины, что и цикл, будет постоянной вели­чиной и не будет содержать цикла; скользящая средняя, более протя­женная, чем период цикла, будет содержать цикл с инвертированной фазой и уменьшенной амплитудой. (Именно из-за последнего свойства в предыдущем шаге сглаживания данных было необходимо использовать скользящую среднюю более короткую, чем самый короткий из отыски­ваемых циклов.)

Центрированная скользящая средняя с длиной, равной длине цикла, не содержит этого цикла. Следовательно, вычитание этой скользящей средней из первоначальных данных удалит тренд и оставит только цикл. Однако если скользящая средняя существенно длиннее, чем отыскиваемый

ГЛАВА 16. анализ циклов фьючерсных рынков 597

Рисунок 16.12.

Не нашли, что искали? Воспользуйтесь поиском: