Задача математического программирования.

Общая постановка.

Задана целевая функция f(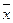) = max/min

Нужно задать ограничения. Если хотя бы одна из функций является нелинейной, то имеем задачу нелинейного программирования.

В качестве отдельного класса у линейного программирования рассматривают задачу геометрического программирования.

Если в целевой функции и неравенствах участвует слагаемое вида ,где c_i – постоянные, положительные коэффициенты, а a_ij – вещественные числа, то имеем задачу геометрического программирования.

Отдельной задачей является целочисленное линейное программирование.

Бывает задача смешанного целочисленного программирования. (люди целые, финансы дробные). – т.е. отдельные переменные принимают только целочисленные значения.

В некоторых задачах отдельные переменные либо коэффициенты могут быть случайными величинами, тогда имеем задачу стохастического программирования.

Пример.

Фирма грузовых перевозок решила приобрести автомобиль для перевозок грузов и выделила 600 000$. Можно приобрести автомобили 3х типов

А – 10 000$

B – 20 000$

C – 23 000$

Стоит проблема, Какого типа грузовики покупать с тем, чтобы получить максимальный эффект. При этом:

А требует 1 водителя и в смену его производительность 2100 тонн*км/смену

B требует 2х водителей, но производительность 2600

C требует 2х водителей, производительность 3780

Число грузовиков не должно превышать 30. Общее число водителей – не больше 145.

В качестве целевой функции выбран следующий критерий:

F = 2100A1 + 4200A2 + 6300A3 + 3600B1 + 7200B2 + 10800B3 + 37800C1 + 7560C2 + 11340C3

A1+A2+A3+B1+B2+B3+C1+C2+C3 <= 30

A1+2A2+3A3+2B1+4B2+6B3 + 2C1+4C2+6C3 <= 145

(A1+A2+A3)*10 + (B1+B2+B3)*20 + (C1+C2+C3)*23 <= 600

Получим12A, 18С

Задача линейного программирования.

Целевая функция

Ограничения:

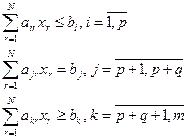
Подобные задачи сводятся к матричному виду и решаются с помощью метода «Симплекс-метод». Он предложен американским исследователем Данцлетом в 60е годы 20го века и является наиболее эффективным методом решения подобных задач.

Существует несколько модификаций симплекс-метода.

Основная идея – берется плоскость (пространство), а далее в силу ограничений выявляется, что область допустимых решений будет представлять собой область (выпуклый многоугольник) в первом квадрате.

В основе – ряд теорем, что решение единственное и находится на угловых точках. Симплекс-метод преобразует неравенства к матрице. С помощью стандартных методов находят угловые точки, затем в какой-то из точек вычисляют целевую функцию. Выбирается определенная последовательность движения от точки к точке. Число точек конечно, но их может быть достаточно много.

Не нашли, что искали? Воспользуйтесь поиском: