Анализ фазовых превращений в двойных сплавах с неограниченной растворимостью компонентов в жидком и твёрдом состояниях

АНАЛИЗ ФАЗОВЫХ ПРЕВРАЩЕНИЙ

В ДВУХКОМПОНЕНТНЫХ СПЛАВАХ

Методические указания к практическим занятиям

по дисциплине «Теория строения материалов»

для студентов всех специальностей

всех форм обучения

Нижний Новгород 2014

Составители: Сорокин В.К., Беляев Е.С., Воскресенская Т.А., Романов А.С.

УДК 621.002.3

Анализ фазовых превращений в двухкомпонентных сплавах: метод. указания к практическим занятиям для студентов всех специальностей всех форм обучения/ НГТУ; сост.: Сорокин В.К., Беляев Е.С., Воскресенская Т.А., Романов А.С. - Н.Новгород, 2014.- 30 с.

Научный редактор С.В. Костромин

Редактор Э.Б. Абросимова

Подп. в печ. 14.07.14. Формат 60х84 1/16. Бумага газетная. Печать офсетная. Печ.л. 1,9 Уч.-изд.л. 1,1. Тираж 300 экз. Заказ

Нижегородский государственный технический университет им. Р.Е. Алексеева.

Типография НГТУ. 603950, Н.Новгород, ул. Минина, 24.

© Нижегородский государственный

технический университет, 2014

Общие сведения

Анализ фазовых превращений в металлических сплавах проводится в следующем порядке:

1) начертить диаграмму фазового равновесия заданной системы, обозначить буквами характерные течки и указать фазы во всех фазо­вых областях;

2) описать, к какому типу относится диаграмма фазового равновесия и указать трёхфазные превращения, имеющие место в системе;

3) подсчитать число степеней свободы во всех фазовых областях для заданного сплава X;

4) по указанию преподавателя определить темп кристаллизации для сплава X;

5) начертить кривую охлаждения сплава Х с учётом темпа кристаллизации в интервале между температурами ликвидуса и солидуса;

6) подчитать по правилу отрезков массы равновесных фаз и массы структурных составляющих при комнатной температуре, исходя из 100 кг первоначального расплава;

7) записать все фазовые превращения при охлаждении сплава Х;

8) зарисовать схемы изменения микроструктуры для сплава Х при охлаждении до комнатной температуры.

Для понимания фазовых превращений необходимо знание основных представлений, используемых при анализе диаграмм состояния.

Простые и сложные вещества, выделенные из окружающего мира реально существующими или воображаемыми поверхностями, называют термодинамической системой. Система характеризуется рядом присущих ей термодинамических параметров: температурой, давлением, концентрацией и др. Совокупность параметров определяет состояние системы. Система может быть гомогенной (однородной), если со­став и свойства однаковы во всех точках, и гетерогенной (неоднородной), если она состоит из нескольких фаз. Под фазой поиимают совокупность материальных частей системы, обладающих одинако­вым или непрерывно от точки к точке изменяющимися термодинамичес­кими параметрами. Фазы отделены одна от другой поверхностями раз­дела, где параметры изменяются скачком.

Такое состояние системы, при которое все термодинамические пара­метры имеют определенные значения, остающиеся при неизменных внеш­них условиях постоянными сколь угодно долго, называется равновесным. Система самопроизвольно переходит в состояние равнове­сия при неизменных внешних условиях. Установление равновесного со­стояния системы произойдет, когда свободная энергия системы достиг­нет минимального значения (рис. 1).

Вещества, минимально необходимые для составления данной систе­мы, называются компонентами. При определенных условиях разные фазы одного и того же вещества могут находиться в равнове­сии друг с другом, соприкасаясь между собой. Равновесие фаз имеет место лишь при определенных значениях параметров системы. Число тер­модинамических параметров системы, которые могут изменяться незави­симо друг от друга без нарушения равновесия фаз и изменения числа фаз, называется числом степеней свободы си­стемы или ее вариантностью. Между числом компонентов К, числом равровесных фаз Ф и вариантностью системы С существует аналитическая зависимость, называемая правилом фаз Гиббса. При по­стоянном давлении С = К – Ф + 1, т.е. число степеней свободы рав­но разности между числом компонентов и числом фаз плюс один.

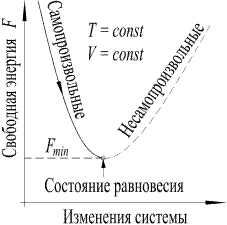
Рис.1

Переход из одной фазы в другую, которые характеризуются изменением объёма и тепловыми эффектами, называются фазовыми переходами I-го рода. К ним относятся превращения твёрдого тела в жидкость, жидкости в пар и т.д. Состояние каждой фазы в системе, состоящей из двух компонентов, может быть изображена геометрически точкой на плоскости, координатами которой служат температура и концентрация (рис. 2). За концентрацию принимается отношение массы одного из компонентов в данной фазе к массе всей фазы. Прямая АВ, отложенная на оси абсцисс, характеризует концентрацию компонентов от 0 до 100%. Конечные точки А и В соответствуют компонентам.

Графически выраженная, зависимость Т-х между значениями переменных, определяющих состояние системы (температура, концентрация), пред­ставляет собой диаграмму состояния системы или диаграмму фазового равновесия. Каждая точка в системе координат Т - х соответствует определенному состоянию системы и называется фигуративной. Процесс нагревания или охлаждения сплава графически изображается перемещением точки, соответствующей данно­му сплаву, вверх или вниз по вертикали. Переход сплава из одного состояния в другое отмечается точками, а совокупность таких точек даёт линии, разделяющие диаграмму состояния на отдельные поля (области). Каждая область диаграммы охватывает все возможные сочета­ния температур и концентраций, отвечающих равновесному существова­нию определённой фазы или фаз.

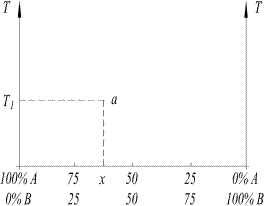
Рис. 2

Анализ фазовых превращений в двойных сплавах с неограниченной растворимостью компонентов в жидком и твёрдом состояниях

Диаграмма фазового равновесия для рассматриваемого случая представлена на рис. 3.

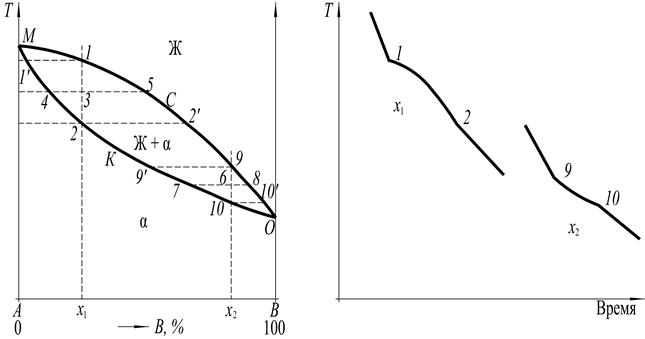
Рис. 3

Как видно, в диаграмме фазового равновесия наблюдается три области состояний: область гомогенного жидкого раствора «Ж» выше линии МСО, область гомогенного твёрдого раствора, обозначенного греческой буквой α, ниже линии МКО и область двухфазного раствора «Ж + α» между линиями МСО и МКО.

Линия МСО представляет собой геометрическое место точек температур начала кристаллизации (или конца плавления) твёрдой фазы α и называется линией ликвидус. Геометрическое место точек температур конца кристаллизации (или начала плавления) твёрдой фазы есть линия МКО, называемая линией солидус.

Выше линии ликвидус жидкий раствор является ненасыщенным, т.е. в нём ещё может раствориться добавочное количество компонентов. На линии ликвидус жидкий раствор становится насыщенным, т.е. таким, в котором компонент при данной температуре уже в большем количестве не растворяется. Ниже линии ликвидус сплавы переходят в двухфазную область «жидкий раствор + твёрдый раствор». Следовательно, линия ликвидус представляет собой геометрическое место точек концентраций жидкого раствора, находящегося в равновесии с твёрдым раствором.

Аналогично линия солидус характеризует концентрацию твёрдого раствора, находящегося в равновесии с жидким раствором. Ниже линии солидус МКО находится область ненасыщенного твёрдого раствора.

Так, для сплава Х ₁ при температуре Т ₃ фигуративной точке 3 системы отвечают на горизонтальной линии фигуративной точке 4 (солидус) и 5 (ликвидус), находящихся в равновесии соответственно твёрдой фазы α и жидкой фазы Ж. Следовательно, концентрация твёрдой фазы выражается точкой 4, а равновесной с ней жидкой фазы – точкой 5.

Фигуративные точки, выражающие концентрации двух равновесных фаз, называются сопряжёнными точками, а кривые, образованные рядами этих точек, называются сопряжённымикривыми. Изотермы, соединяющие фигуративные точки двух фаз, находящихся в равновесии (т.е. сопряжённые точки), называются конодами. Для рассмотренного примера конодой будет линия 4-5. Следовательно, при температурах Т ₁ и Т ₂ конодами будут линии 1’-1 и 2-2’.

Соотношение количеств находящихся в равновесии фаз определяется правилом отрезков (или рычага):

,

т.е. массы фаз, находящиеся в соотношении, обратно пропорциональны отрезкам, на которые фигуративная точка 3 делит изотерму (коноду), соединяющую сопряжённые точки 4 и 5.

Массу каждой отдельно взятой фазы можно определить из следующих соотношений:

т.е. для определения количества жидкой фазы необходимо взять отношение длины отрезка 4-3, примыкающего к области твёрдой фазы, к длине коноды 4-5; для подсчёта твёрдой фазы берётся отношение длины отрезка 3-5, примыкающего к области жидкой фазы к длине коноды 4-5.

Рассмотрим фазовые превращения, происходящие в рассматриваемой системе, на примере охлаждения сплава состава Х ₁. Выше точки 1 сплав находился в области однофазного ненасыщенного жидкого раствоpa. Применяя правило фаз, будем иметь для однофазной области «Ж» число степеней свободы:

С_Ж = К – Ф + 1 = 2 – 1 + 1 = 2.

Так как С = 2, то возможно в пределах области жидкой фазы, выше линии ликвидус МСК, изменять произвольно по нашему выбору, одновременно температуру и концентрацию, не нарушая равновесно­го однофазного состояния системы. Геометрически это означает, что фигуративная точка может быть смещена в любом направлении в области выше линии ликвидус МСК.

В интервале температур Т ₁- Т ₂ сплав находится в двухфазной об­ласти «жидкий раствор + твердый раствор» и число степеней свободы по правилу фаз равно:

С_Ж+α = К – Ф + 1 = 2 – 2 + 1 = 1.

При С = 1 допустимо произвольно изменять только один параметр состояния: температуру или концентрацию одного из компонентов. Геометрически это значит, что фигуративная точка в области между МСО и МКО может быть смещена или по вертикали (шкала температур) без изменения состава сплава, или по изотерме, когда изменяется состав сплава при постоянной температуре. Каждой температуре отве­чает новая, строго определенная концентрация жидкой и находящейся с ней в равновесии твердой фазы.

При температуре ниже точки 2 сплав находится в области однофазного ненасыщенного твердого раствора и число степеней свободы:

С_α = К – Ф + 1 = 2 – 1 + 1 = 2.

Следовательно, возможно одновременно изменять температуру и концентрацию, сохраняя равновесное состояние системы.

Далее построим кривую охлаждения сплава состава Х ₁. В соответствии с правилом фаз кристаллизация твердого раствора происходит в некотором интервале температур T ₁- Т ₂, называемой интервалом кристаллизации (С = К – Ф + 1 = 2 – 2 +1 = 1), и на кривой охлаждения будут две критических точки 1 и 2 (см. рис. 3). Ход кривой охлаждения в интер­вале температур между точками ликвидуса 1 и солидуса 2 зависит от темпа (интенсивности) кристаллизации. Темп кристаллизации ха­рактеризует увеличение в сплаве количества кристаллов при пониже­нии температуры, т.е. скорость кристаллизации по температуре (про­изводная массы по температуре dM / dT). Для сплавов различного химического состава при понижении температуры на одинаковую долю ин­тервала кристаллизации (например, на 1/2 этого интервала) кристал­лизуется различное количество всей массы сплава и характер кривых охлаждения будет различен.

Так, для сплава X ₁ количество твердой фазы при Т ₃ (1-3 = 3-2) определяется по правилу отрезков следующим отношением:

В этом сплаве в начальной стадии кристаллизации приращение мас­сы твердой фазы изменяется с понижением температуры очень значи­тельно, поэтому на кривой охлаждения четко выявляется точка ликви­дуса 1; в интервале температур Т ₁- Т ₂ кривая охлаждения является выпуклой (рис. 3).

У сплава Х ₂ количество твердой фазы при T ₆ (9-6 = 6-10):

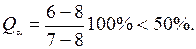
Приращение массы в начальный период кристаллизации незначи­тельное, точка ликвидус 9 выявляется нечетко и кривая охлаждения в интервале температур Т ₄- Т ₅ является вогнутой.

После построения кривой охлаждения рассмотрим процессы, проис­ходящие при охлаждении сплава состава X ₁. Выше температуры ликви­дуса T ₁ сплав находится в области однофазного ненасыщенного жидко­го раствора. При T ₁ жидкий раствор становится насыщенным.

Ниже T ₁ начинается фазовый переход жидкой фазы в твердую (твер­дый раствор), который заканчивается при температуре солидуса T ₂. Концентрация жидкой и твердой фазы изменяется при этом по сопряженным кривым 1 - 2’ и 1’ - 2, соответственно. Следовательно, концент­рация жидкой фазы меняется по отрезку 1 - 2’ кривой ликвидуса, а твердой фазы – по отрезку 1’ - 2 кривой солидуса.

Процесс фазового перехода записывают следующим образом:

.

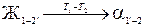В левой части записывается исходная фаза, а в правой – конеч­ная. Стрелка означает фазовый переход, a T ₁ и Т ₂ над стрелкой – температуры начала и конца фазового перехода, а индексы 1’-2 фазы в левой части показывают изменение концентрации исходной фазы в интервале температур Т ₁ – Т ₂ фазового перехода, а индексы 1’-2 фа­зы α в правой части – соответственно изменение концентрации конечной фазы.

Представленная запись читается так: жидкая фаза в интервале температур Т ₁- Т ₂ переходит в твёрдую фазу α, причём концентрация жидкой фазы изменяется по линии 1-2’, а твёрдой фазы – по линии 1’-2.

Ниже температуры солидуса Т ₂ происходит охлаждение однофазного ненасыщенного твёрдого раствора. Аналогично анализируется процесс фазового перехода и для сплава состава Х ₂.

Не нашли, что искали? Воспользуйтесь поиском: