
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Контрольное задание № 3
([2] – 4.4, [1] –11.4)
1. Закон распределения
([2] – 4.4.2, [1] –11.4.2)
Стационарный случайный процесс  описан плотностью вероятности
описан плотностью вероятности 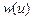 (табл. 4.3); параметры функции
(табл. 4.3); параметры функции 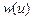 приведены в табл. 4.4.
приведены в табл. 4.4.
Требуется:
а) получить выражение для функции распределения  ;
;
б) построить график  ;
;
в) найти выражение для характеристической функции 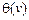 и энтропии Н.
и энтропии Н.
Методическое указание
Характеристики и параметры различных законов распределения приведены в [8, 9], а нормального закона – в прил. П.7.
Таблица 4.3
| Номер вариа-нта | Закон распределения | Плотность вероятности 
| ||
| Аналитическая запись | График | |||
| Равномерный | 
| 
| ||
| Нормальный (Гаусса) |  
| 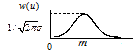
| ||
| Коши | 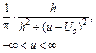
| 
| ||
| Релея |  , , 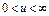
| 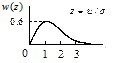
| ||
| Экспоненциальный | 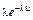 , , 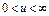
| 
| ||
| Лапласа | 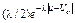 , , 
| 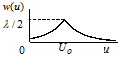
| ||
| Симпсона (треугольный) | 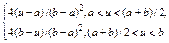
| 
| ||
| Арксинуса |   , , 
| 
| ||
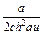 , , 
| 
| |||
| Усеченный нормальный | 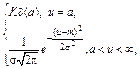 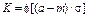
| 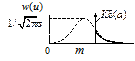
| ||
Таблица 4.4
| Параметр | Номер подварианта | |||||||||

| 0.0 | 0.1 | 0.15 | 0.20 | 0.25 | 0.3 | 0.0 | 0.1 | 0.15 | 0.2 |

| 0.31 | 0.25 | 0.20 | 0.15 | 0.10 | 0.0 | 0.0 | 0.1 | 0.10 | 0.2 |
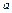 , B , B
| 0.2 | 0.4 | 0.60 | 0.80 | 1.00 | 1.2 | 1.4 | 1.6 | 1.80 | 2.0 |
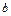 , B , B
| 1.2 | 1.6 | 2.00 | 2.40 | 2.80 | 3.2 | 3.6 | 4.0 | 4.40 | 4.8 |
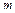 , B , B
| 0.0 | 0.0 | 0.00 | 0.50 | 0.50 | 0.5 | 1.0 | 1.0 | 1.00 | 2.0 |
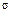 , B , B
| 0.5 | 1.0 | 2.00 | 0.50 | 1.00 | 2.0 | 0.5 | 1.0 | 2.00 | 2.0 |
 , B , B
| 0.5 | 1.0 | 2.00 | 0.50 | 1.00 | 2.0 | 0.5 | 1.0 | 2.00 | 2.0 |
 , B , B
| 0.0 | 0.0 | 0.00 | 0.50 | 0.50 | 0.5 | 1.0 | 1.0 | 1.00 | 2.0 |
 , 1/B , 1/B
| 0.5 | 1.0 | 1.50 | 2.00 | 2.50 | 3.0 | 3.5 | 4.0 | 4.50 | 5.0 |
 , B , B
| 5.0 | 4.5 | 4.00 | 3.50 | 3.00 | 2.5 | 2.0 | 1.5 | 1.00 | 0.5 |
2.Моментные функции. Стационарность и эргодичность
([2] – 4.4.3. [1] – 11.4.3)
В табл. 4.5 задан процесс  . При описании
. При описании  приняты следующие обозначения:
приняты следующие обозначения:
 и
и  – детерминированные функции времени, описываемые с помощью постоянных параметров
– детерминированные функции времени, описываемые с помощью постоянных параметров 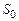 ,
,  ,
,  ,
,  ,
, 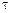 и
и  (табл. 4.5);
(табл. 4.5);
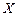 и
и 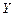 – некоррелированные случайные величины с известными математическими ожиданиями
– некоррелированные случайные величины с известными математическими ожиданиями  и
и  и дисперсиями
и дисперсиями  и
и  ;
;
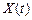 и
и  – некоррелированные эргодические случайные процессы, которые соответственно имеют известные математические ожидания
– некоррелированные эргодические случайные процессы, которые соответственно имеют известные математические ожидания  и
и  дисперсии
дисперсии  и
и  и автокорреляционные функции
и автокорреляционные функции 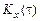 и
и  .
.
Требуется:
а) определить математическое ожидание  , дисперсию
, дисперсию  и корреляционную функцию
и корреляционную функцию  процесса
процесса  ;
;
б) классифицировать процесс  по признакам стационарности и эргодичности.
по признакам стационарности и эргодичности.
Таблица 4.5
| Номер варианта | 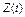
| Номер варианта | 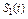
| 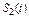
|

| 
| 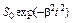
| ||
 + + 
| 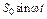
| 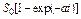
| ||

| 
| 
| ||
 + + 
| 
| 
| ||
 + + 
| 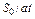
| 
| ||

| 
| 
| ||

| 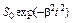
| 
| ||

| 
| 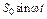
| ||

| 
| 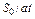
| ||

| 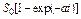
| 
|
Не нашли, что искали? Воспользуйтесь поиском: