Определение ускорения свободного падения с помощью математического маятника

ВНИМАНИЕ! Подключение лабораторной установки к сети обязательно должно проводиться в присутствии преподавателя или лаборанта!

ПОДГОТОВКА К ЛАБОРАТОРНЫМ РАБОТАМ.

1) При подготовке к выполнению лабораторной работы и к ее защите необходимо изучить краткую теорию и описание к работе; рассмотреть указанный материал по литературе. Изучение материала рационально строить в соответствии с приведенными контрольными вопросами.

2) Подготовить заготовку по лабораторной работе, в которую необходимо включить:

а) цель работы, приборы и оборудование;

б) основные расчетные соотношения с пояснениями, схемы установок;

в) заготовить таблицы для результатов измерений.

ЛАБОРАТОРНАЯ РАБОТА № 72

Гармонические колебания маятников

Математический маятник

Физический маятник

ЦЕЛЬ РАБОТЫ

1. Определить ускорения свободного падения с помощью математического маятника.

2. Определить периоды и приведенные длины физического маятника.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ

1. Математический маятник, линейка, секундомер.

2. Физический маятник, линейка, секундомер.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какой маятник называется физическим, математическим?

2. При каком условии маятник совершает гармонические колебания?

3. Выведете дифференциальное уравнение гармонического колебания маятника.

4. Решение уравнения гармонического колебания маятника.

5. Дайте определения амплитуды, периода, частоты и фазы колебаний.

6. Период колебаний физического, математического маятников.

7. Приведенная длина физического маятника.

8. Теорем Штейнера.

9. Выведете расчетную формулу для определения периода колебаний физического маятника.

10. Выведете расчетную формулу для определения ускорения свободного падения с помощью математического маятника.

11. Почему практическое определение ускорения свободного падения из формулы 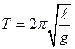приводит к большим погрешностям?

Определение ускорения свободного падения с помощью математического маятника

Для определения ускорения свободного падения при помощи математического маятника на основе формулы

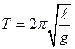
требуется определить опытным путем период колебаний Т и длину математического маятника.

Для определения периода колебаний 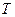посредством секундомера определяется время полных колебаний, после чего подсчитывается период:

.

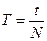Определение длины маятника довольно трудная задача. Шарик имеет размеры в несколько сантиметров и его центр тяжести не совпадает с геометрическим центром шарика. Таким образом, при измерении длины маятника получается большая, в несколько сантиметров, погрешность.

Определить ускорение свободного падение можно и без непосредственного измерения длины математического маятника. Для этого измеряют время полных колебания маятника сначала при длине . Пусть период колебаний для этого случая будет . Затем изменяют длину маятника и снова определяют период колебаний. Пусть период колебаний в этом случае будет , а длина маятника, соответствующая этому периоду, :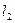

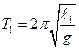
Возводя в квадрат и вычитая, получим

(1)

Из равенства (1) видно, что для определения ускорения свободного падения 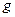надо опытным путем найти периоды и маятников различных длин и разность этих длин. Разность можно заменить расстоянием от нижней точки шарика в первом опыте до нижней точки во втором опыте, т.е. разностью отсчетов по шкале в первом и втором опытах . Погрешность этого измерения равна погрешности измерительного прибора – линейки.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Измеряют время 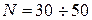полных колебания маятника. Для этого отводят маятник на небольшой угол порядка и отпускают, предоставив ему совершать свободные колебания. Измерения проводят раз . Измеряют отсчет по шкале 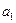– расстояние от точки подвеса до нижней точки шарика.

2. Вычисляют среднее значение времени .

Период вычисляют по формуле .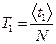

3. Устанавливают другую длину маятника и измеряют отсчет по шкале . должно быть около 40 – 50 см. При этом 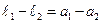. Повторяют измерения п.1, 2.

4. Вычисляют ускорение свободного падения, пользуясь формулой (1). По методу Стьюдента обрабатывают результаты прямых и косвенных измерений. (см приложение). Результаты занести в таблицу.

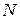
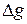		с	с	с	с		м/с2		м/с2

5. Сравнить полученное значение с табличным значением значения ускорения свободного падения для нашей широты . Сделать вывод.

Не нашли, что искали? Воспользуйтесь поиском: