
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Действия над матрицами
Содержание
Лабораторная работа № 1.
Работа в командном окне системы MatLAB.. 3
Цель работы.. 3
Введение. 3
Типы данных. 4
Действия над матрицами. 4
Построение графиков. 6
Поиск решения уравнения. 7
Задание на лабораторную работу. 8
Литература к лабораторной работе №1. 8
Лабораторная работа № 2.
Построение трехмерных графиков. Программирование в MatLAB.. 9
Цель работы.. 9
Построение трехмерных графиков. 9
Программирование в системе MatLAB.. 10
Задание на лабораторную работу. 13
Литература к лабораторной работе №2. 14
Лабораторная работа № 3.
Вычисление определенных интегралов в среде MatLAB.. 15
Цель работы.. 15
Вычисление определенных интегралов. 15
Аналитические вычисления. 16
Решение систем линейных уравнений. 16
Задание на лабораторную работу. 16
Литература к лабораторной работе №3. 17
Лабораторная работа № 4.
Хаотические свойства нелинейных систем.. 18
Цель работы.. 18
Введение. 18
Дискретные отображения. 18
Порядок построения паутинной диаграммы.. 20
Задание на лабораторную работу. 20
Варианты заданий. 21
Пояснения к выполнению лабораторной работы.. 21
Литература к лабораторной работе №4. 21
Лабораторная работа № 5.
Дискретные отображения и бифуркационные диаграммы.. 22
Цель работы.. 22
Основные сведения о бифуркационных диаграммах. 22
Порядок построения бифуркационной диаграммы.. 22
Задание на лабораторную работу. 23
Варианты заданий. 23
Пояснения к выполнению лабораторной работы.. 23
Литература к лабораторной работе №5. 24
Лабораторная работа № 6.
Карты динамических режимов и решетки связанных отображений. 25
Цель работы.. 25
Основные сведения о картах динамических режимов. 25
Решетки связанных отображений. 26
Задание на лабораторную работу. 28
Литература к лабораторной работе №6. 29
Лабораторная работа № 7.
Фазовые портреты динамических систем. 30
Цель работы.. 30
Основные сведения о фазовом пространстве. 30
Построение аттракторов. 31
Фрактальная размерность и показатель Хёрста. 31
Задание на лабораторную работу. 32
Пояснения к выполнению лабораторной работы.. 32
Литература к лабораторной работе №7. 33
Лабораторная работа № 1.
Работа в командном окне системы MatLAB
Цель работы
Целью данной лабораторной работы является ознакомление с основами работы в среде MatLAB: изучение типов используемых данных, работа с массивами, построение графиков и т.д.
Введение
После запуска системы MatLAB на экране появиться окно, показанное на рис. 1.1, предназначенное для ввода команд и вывода результатов.
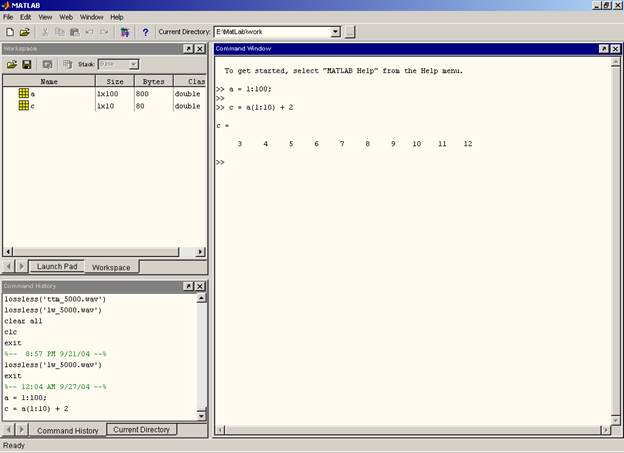
Рис. 1.1. Командное окно системы MatLAB
Знак «>>» показывает готовность системы к выполнению введенных команд. Набрав простейшие математические выражения в естественной форме записи, сразу же вычисляется результат. Это выражение может быть записано в двух видах: <Выражение> или <Имя переменной> = <Выражение>. Во втором случае результат не только вычисляется, но и присваивается указанной переменой. MatLAB не требует от пользователя специальных команд для объявления переменных, они создаются автоматически при первом указании пользователем их имени. В первом случае на самом деле результат выражения присваивается специальной служебной переменной имеющей имя ans, так же можно использовать эту переменную в расчетах. Если нет необходимости, что бы MatLAB выводил результаты промежуточных выражений на экран, то необходимо поставить в конце выражения символ «;».
Типы данных
Фактически MatLAB содержит один тип данных - массив или матрица. Массив это группа ячеек памяти, имеющие одно имя. Массивы бывают одномерные - строка или столбец, прямоугольные, квадратные (число строк рано числу столбцов). Когда Вы указываете переменную и присваиваете ей одно число, фактически MATLAB создает матрицу из одной строки и одного столбца.
Ниже приведены примеры столбца – а, строки – б, прямоугольной матрицы – в, квадратной матрицы – г, матрицы единичной размерности – е (простой переменой).
| а | б | ||||||||||||||||||
| е | |||||||||||||||||||
| в | |||||||||||||||||||
| г |
Рис. 1.2. Виды матриц
Помимо одномерных и двумерных матриц MatLAB поддерживает ряд других типов данных. К ним относятся многомерные массивы, строки, структуры, массивы ячеек, а также объекты.
Действия над матрицами
Создание матриц
Простейшей операций с матрицей является ее создание. Для создания строки необходимо указать его имя, знак равенства и в квадратных скобках через запятую или через пробел перечислить значения элементов:
>> А=[1 2 3 4 5];
В случае если необходимо создать столбец чисел, то в качестве разделителя выступает символ точка с запятой:
>> B=[1; 3; 5; 7];
Для создания квадратной или прямоугольной матрицы понадобится чередовать оба этих способа.
>> С=[1 2 3; 4 5 6; 7 8 9];
2. Создание матриц специального вида:
Для генерации векторов пользователю предоставляется следующая команда: <Имя вектора>=<Начальное значение>:<Шаг>:<Конечное значение>
>> Х=6: 0.2: 26;
В результате получиться вектор X следующего вида:
| 6.2 | 6.4 | 6.6 | … | 25.6 | 25.8 |
В математике часто встречаются матрицы специального вида. Ниже приведен ряд из них:
Единичная матрица, рис. 1.3.а. В единичной матрице все элементы равны нулю, кроме элементов стоящих на главной диагонали (матрица является квадратной). Для создания единичной матрицы Вам необходимо подать команду <Имя матрицы>=eye(<Размер>);
>> a = eye(4);
Матрица со всеми единицами, рис. 1.3.б. Эта матрица содержит единицы во всех ячейках. Для создания матрицы необходимо указать <Имя матрицы>=ones(<Кол-во строк>, <Кол-во столбцов>);
>> b = ones(3, 4);
Нулевая матрица, рис. 1.3в. Эта матрица содержит во всех своих ячейках одни нули. Для создания необходимо выполнить следующую команду: <Имя матрицы>=zeros(<Кол-во строк>, <Кол-во столбцов>);
>> c =zeros(4, 2);
Случайная матрица, рис. 1.3.г. Все значения этой матрицы получаются с генератора случайных чисел. Для создания такой матрицы необходимо дать следующую команду: <Имя матрицы>=rand(<Кол-во строк>, <Кол-во столбцов>);
>> d =rand(3, 4);
| а | б | в | г |
Рис. 1.3. Специальные матрицы.
Не нашли, что искали? Воспользуйтесь поиском: