Дискретные отображения

Рассмотрим функцию, отображающую некоторое множество само с себя:

.

Итерация f ⁽ⁿ⁾ функции f определяется как композиция f с самой собой n раз:

, .

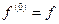Итерацию можно выразить другим способом: .

Поскольку каждая точка под действием итераций функции f перемещается по множеству М, то функция f задает дискретную динамическую систему, т.е. некое движение на множестве М с течением дискретного времени n. Если для некоторой точки определены все итерации , то множество называется орбитой точки x под действием функции f.

Точка x называется неподвижной точкой функции f, если для любого n. Неподвижная точка x функции f называется притягивающей, если все точки из некоторой ее окрестности стремятся к x под действием итераций функции f; и отталкивающей, если все точки из некоторой окрестности покидают эту окрестность под действием итераций. Если неподвижная точка является притягивающей либо отталкивающей, то она также называется гиперболической.

Точка x называется периодической точкой функции f периода k, если , причем при i < k. Орбита периодической точки состоит из k точек и называется циклом периода k. Точка x является периодической точкой функции f периода k, если она является неподвижной точкой итерации , но не является периодической точкой итераций с меньшими номерами.

Дав основные понятия, можно вернуться к исследованию логистической функции. Исследуемая функция является функцией одного параметра λ. Наша задача выяснить, как меняются орбиты точек, при изменении параметра λ. Чаше всего, при малом изменении параметра динамика, определяемая функцией, меняется мало. Немного изменяются значения неподвижных, периодических точек. Однако при некоторых значениях параметра происходит резкое изменение качественной картины, например, изменяется количество неподвижных точек, меняется их характер (притягивающие превращаются в отталкивающие). Скачкообразное изменение качественного поведения системы при плавном изменении параметра называется бифуркацией.

Рассмотрим, что будет происходить с точками из интервала [0;1] под действием итераций логистической функции.

При 0 < λ < 1 точка x = 0 является притягивающей, и каждая точка выбранного отрезка под действием итераций стремится к ней. При λ = 1 происходит бифуркация, и точка x = 0 перестает быть притягивающей.

При 1 < λ < 3 точка x = 0 является отталкивающей, а точка – притягивающей неподвижной точкой.

Следующая бифуркация происходит при λ = 3, когда точка перестает быть притягивающей и превращается в отталкивающую при λ > 3. Поскольку теперь обе точки x₁ и x₂ являются отталкивающими, логично предположить о наличии некого притягивающего объекта между ними. Так оно и происходит. При λ > 3 появляются еще две неподвижные точки, которые не являются неподвижными точками исходной функции. Они образуют цикл периода 2. Таким образом, имеет место бифуркация удвоения периода.

При дальнейшем увеличении параметра λ можно наблюдать и дальнейшие бифуркации удвоения периода. Для того чтобы наблюдать весь этот каскад бифуркаций можно провести следующий эксперимент. Выберем какое-либо начальное значение x и проделаем над ним 100-200 итераций отображения логистической функции. Затем отложим значения следующих 100-200 итераций по вертикальной оси, а значение параметра λ, при котором производились вычисления, – по горизонтальной. По оси λ пройдем отрезок от 2,9 до 4 с небольшим интервалом, например 0,01. Полученное множество называется бифуркационной диаграммой логистической функции.

Бифуркационная диаграмма позволяет проследить за развитием системы при плавном изменении параметра. При фиксированном значении параметра за орбитами точек позволяет проследить паутинная диаграмма (диаграмма Ламерея), изображенная на рисунке 1. Построение паутинной диаграммы позволяет выявить различные эффекты, незаметные на бифуркационной.

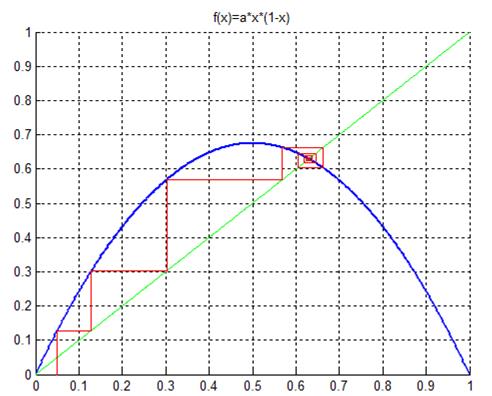
Рис. 4.1. Паутинная диаграмма логистической функции при λ = 2.7

Не нашли, что искали? Воспользуйтесь поиском: