Решетки связанных отображений

Для описания сложной динамики и хаоса в распределенных системах различной природы (гидродинамическая турбулентность, электронные устройства, системы нелинейной оптики, химические системы реакция – диффузия, модели биологических популяций) могут привлекаться системы уравнений с частными производными, цепочки нелинейных осцилляторов, решетки связанных отображений, клеточные автоматы. Если речь идет о качественном понимании сложной пространственно-временной динамики, то во многих случаях предпочтительно иметь дело не с непрерывной средой, а с решеточными моделями.

Решетки связанных отображений введены в рассмотрение в начале 80-х годов. Представим себе одномерную цепочку или двумерную решетку, в которой каждой ячейке сопоставлена система с дискретным временем, например, квадратичное отображение. Пусть, далее, каждый элемент каким-то образом связан со своими соседями, так что мгновенное состояние соседних ячеек оказывает влияние на состояние данного элемента в следующий момент времени.

Иногда переход к решетке может рассматриваться как приближенный метод описания непрерывной системы. В других случаях решеточная модель может быть подходящей по самому существу задачи. Например, в физике твердого тела естественная дискретизация обеспечивается наличием кристаллической решетки.

Для задания взаимодействия между элементами решетки достаточно задания 2-х типов связи: инерционной и диссипативной; величина связи задается при помощи коэффициентов E1 и E2. Смысл и свойства диссипативной и инерционной связи рассмотрены в табл. 1.

Таблица 1. Диссипативная и инерционная связь

Рассмотрим систему из двух элементов, каждый из которых описывается квадратичным отображением 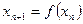, 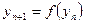Пусть, например, речь идет о двух биологических популяциях, численность которых изменяется из года в год согласно этим уравнениям.
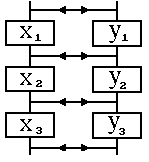
Один способ ввести связь состоит в предположении, что организмы сначала размножаются (гибнут), оставаясь в своей популяции, а потом на некоторое время получают возможность мигрировать между популяциями («сначала размножаются, потом расползаются»). На следующий год цикл повторяется. Уравнение имеет вид 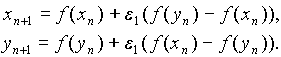Этому соответствует вторая картинка. Такая связь стремится выровнять мгновенные состояния подсистем, и ее естественно назвать диссипативной.
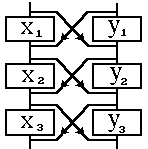
Другой способ: организмы имеют возможность миграции, минуя цикл размножения и гибели в «своей» популяции. Уравнение имеет вид 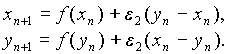Такая связь способствует сохранению памяти о состоянии на предыдущем шаге, и ее естественно именовать инерционной.
Наконец, могут присутствовать оба типа связи, это комбинированная связь: 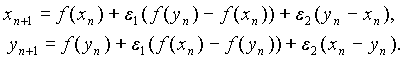То, что других типов связи вводить не нужно, и данное уравнение служит в определенном смысле универсальной моделью связанных систем, следует из ренормгруппового анализа.

Исследования решеток связанных отображений позволяет обнаружить явления и эффекты, недостижимые при моделировании одиночных отображений. Например, на Рис. 5 приводятся карты динамических режимов при различных значениях параметров связи Е1 и Е2 для следующей решетки связанных отображений:

.

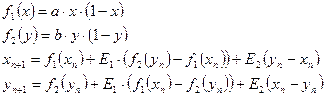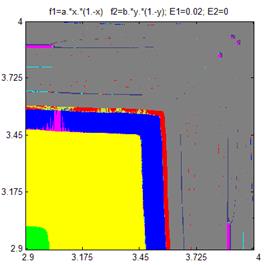
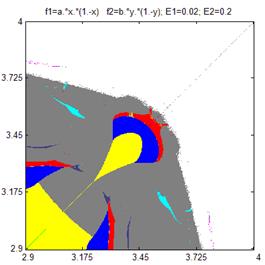
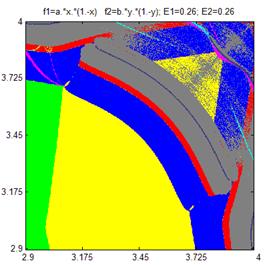
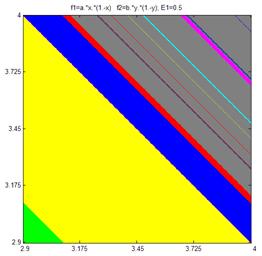
Рис. 6.3. Карты динамических режимов для решетки из двух логистический функций
при различных значениях параметров связи.

Для построения карт динамических режимов и бифуркационных диаграмм для решетки из 2-х связанных отображений предназначена программа DinMap2. Отображения имеют два вида связи: инерционную и диссипативную; величина связи задается при помощи коэффициентов E1 и E2. Общее количество параметров двух отображений – 2 (без учета коэффициентов связи).

Не нашли, что искали? Воспользуйтесь поиском: