Значения величин для вычисления коэффициента корреляции

Событие (S)	Фактор (F)	Количество событий по строке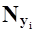
X1=1	X2=0
Y1 = 1	N11	N12
Y2 = 0	N21	N22
Количество событий по столбцу	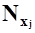		Всего N

Расчет производится в следующем порядке:

1. Найти условные математические ожидания M(S/x) и M(F/y)

при x₁=1

M(S/x₁) = (1/Nx₁)(N₁₁*y₁ + N₂₁*y₂) = N₁₁*y₁/Nx₁ = N₁₁/Nx₁

при x₂=0 (2.14)

M(S/x₂) = (1/Nx₂)(N₁₂*y₁ + N₂₂*y₂) = N₁₂*y₁/Nx₂ = N₁₂/Nx₂

при y₁=1

M(F/y₁) = (1/Ny₁)(N₁₁*x₁ + N₁₂*x₂) = N₁₁*x₁/Ny₁ = N₁₁/Ny₁

при y₂=0 (2.15)

M(F/y₂) = (1/Ny₂)(N₂₁*x₁ + N₂₂*x₂) = N₂₁*x₁/Ny₂ =N₂₁/Ny₂

По полученным значениям (2.14) и (2.15) строятся линии регрессии, которые в данном случае представляют собой пересечение двух отрезков, проведенных через две точки каждый (рис. 2.8).

Рис. 2.8. Линии регрессии, характеризующие зависимость S от F

Угол  между линиями регрессии характеризует силу связи между случайными величинами F и S. Если между случайными величинами существует функциональная зависимость, то  = 0,т.е. обе линии сливаются.При r_xy =0 линии регрессии взаимно перпендикулярны и параллельны соответствующим координатным осям. Угол  определяется как разница между углами наклона соответствующих линий регрессии

2. Определить математические ожидания M(F) и M(S):

; . (2.16)

3. Определить корреляционный момент:

=

+ . 2.17)

4. Определить значения дисперсии D(F) и D(S)

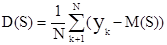(2.18)

и среднеквадратических отклонений:

= (2.19)

5. Определить коэффициент корреляции:

(2.20)

6. Вычислить коэффициент регрессии:

(2.21)

Вторым подходом к определению взаимосвязей между различными, случайными величинами принято определение коэффициента корреляции между количеством случайных событий и факторов, произошедших за месячные промежутки времени за рассматриваемый 5-летний период. Таким образом, получается k столбцов f₁, f₂,…,f_k, каждый из которых содержит по 60 чисел (Приложение 1).

Если имеется два столбца чисел, имеющих значения f₁(x₁, x₂,…, x_i) и f₂(y₁, y₂,…, y_j); (1  i  60); (1  j  60), то взаимосвязь между ними определяется корреляционным коэффициентом [15].

Коэффициент корреляции определяется в следующем порядке:

- определяются математические ожидания факторов M(F) и событий M(S);

; ; (2.22)

- определяется корреляционный момент:

; (2.23)

- определяются среднеквадратические отклонения:

; (2.24)

- определяется коэффициент корреляции:

(2.25)

Вычисления коэффициентов корреляции между различными факторами и событиями производятся на базе статистических данных, полученных на основании расследования авиационных происшествий и инцидентов. Из анализа исключаются факторы, которые, по данным МАСУ «Безопасность» проявились в единичных случаях, а соответственно оценка их влияния на возникновение неблагоприятных событий статистическим путем практически невозможна. Также исключено распределение событий по типам ВС, т.к. отсутствуют данные по их налету.

Если какая-либо группа однородных факторов является факторами условий для возникновения определенного следствия (аварийного фактора), то они суммируются и определяются единым символом, что соответствует выполнению условия (2.12).

Оценка взаимосвязи между двумя случайными событиями посредством условных вероятностей позволяет проследить два направления:

- вероятность возникновения события А если произошло событие В, т.е. Q(А/В) и

- вероятность присутствия события В, если произошло событие А, т.е. Q(B/A).

Первый подход позволяет оценить переход какого-либо аварийного фактора F_i в неблагоприятное событие (К, А, СИ, И), т.е. характеризовать опасность этого фактора по схеме (рис. 2.9)

Рис. 2.9. Схема оценки опасности аварийного фактора F_i

Второй подход позволяет оценить степень «присутствия» какого-либо аварийного фактора F _i при возникновении неблагоприятного события S, т.е. определить частоту появления какого-либо фактора в данном виде неблагоприятного события (рис. 2.10).

Рис.2.10. Схема оценки частоты повторяемости аварийного фактора F_i в определенном виде неблагоприятного события S

Факторы U_j (условия труда) являются условием наступления факторов F_i (аварийных факторов). Для возникновения фактора F_i при наличии фактора условия U_j должно соблюдаться логическое условие:

ЕСЛИ (И(U_j=1;F_i=1);1;0) (2.26)

Отношения количества аварийных факторов F_i, проявившихся в данных условиях Uj дает условную вероятность проявления аварийных факторов F _i в U _j условиях:

(2.27)

С учетом схемы (рис. 2.9) и условия, аналогичного (2.26) определяются условные вероятности перехода аварийного фактора F_i в неблагоприятное событие (S).

Установлению присутствия аварийного фактора F_i при неблагоприятном событии S соответствует логическое условие

ЕСЛИ (И(S=1;F_i=1);1;0) (2.28)

По полученным результатам можно определить факторы, каких служб приводят к неблагоприятным событиям. Используя условия аналогичные (2.28), определяется, какие факторы приводят к неблагоприятным событиям в данных службах.

Так как в данном исследовании принимались в расчет условия труда персонала гражданской авиации, то с учетом формулы (2.12) можно определить процент неблагоприятных авиационных событий, которые происходят из-за неудовлетворительных условий труда.

Повышение безопасности полетов путем улучшения условий труда возможно при устранении факторов условий, которые приводят к ошибкам или нарушениям операторов, приводящим к возникновению особых ситуаций. Не всегда часто повторяющиеся сложные условия трудовой деятельности приводят к особым ситуациям. Необходимо выявить те факторы условий, которые наиболее существенно влияют на работу операторов и приводят к наиболее тяжелым событиям. Применяя ретроспективный метод можно определить цепочку причинно-следственных связей, приводящих к неблагоприятным авиационным событиям.

Для определения доминирующих факторов применима схема (рис.2.11).

Рис. 2.11. Ретроспективная схема определения доминирующих факторов

Для выявления возможной причины возникновения аварийного фактора F_i, необходимо проводить аттестацию рабочих мест авиационного персонала и учитывать ее результаты в материалах расследования неблагоприятных событий.

ЗАКЛЮЧЕНИЕ

Представленные результаты исследования позволяют сделать следующие основные выводы.

Сложившиеся ограничения в обеспечении безопасности полетов в значительной степени обусловлены отсутствием сертификационных требований по надежности как к элементам авиационной системы, обеспечивающих полет, так и ко всему полету в целом. В равной степени это касается факторов безопасности жизнедеятельности. Принципиально разработка сертификационных требований возможна при условии создания физической модели развития опасности, позволяющей формализовать связь надежности элементов АС с безопасностью полета, и решения проблемы сертификации по критериям надежности деятельности человека.

Первое условие выполнимо, если воспользоваться ситуационной моделью развития опасности в полете, в которой классификация особых ситуаций в отличии от существующего вероятностного подхода строится по принципу их соотнесения с резервными средствами (компенсаторными возможностями) АС, адекватными возникшему состоянию.

Для реализации второго условия необходимо реально выявить гарантируемые возможности человека применительно ко всем возникающим в полете состояниям. Число таких состояний, нуждающихся в самостоятельной сертификации, устанавливается принятой моделью развития опасности. В общем случае к ним относятся основные и резервные функции пилота в нормальных условиях и в идентифицируемых классификатором особых ситуациях.

Особенностью влияния человека на надежность полета является высокая вероятность провоцирования им множественных отказов в системе. По этой причине происходит более 70% всех тяжелых АП. Это обстоятельство может быть учтено разделением всех элементов АС и их функций на основные и компенсаторные, подлежащие самостоятельной и независимой сертификации.

Исследования трудовой деятельности авиационного персонала показали, что влияние на факторы безопасности жизнедеятельности, такие как условия и охраны труда на рабочих местах обеспечивают повышение качества труда, что способствует повышению уровня безопасности полетов. В ходе исследований разработана структурно-функциональная модель системы "человек - среда", позволяющая проследить причинно-следственные связи и последовательные стадии формирования различных состояний организма работающих, которые возникают под влиянием факторов производственной среды. Показана зависимость между условиями труда на рабочих местах и безопасностью полетов, что позволило разработать математическую модель оценки влияния факторов безопасности жизнедеятельности, к которым относятся и факторы условий труда на безопасность производственного процесса. Экспериментальные исследования, проведенные с помощью разработанной математической модели, показали, что улучшение условий трудовой деятельности обеспечивают снижение аварийности на воздушном транспорте.

Создание единого информационного поля по факторам безопасности полетов и безопасности жизнедеятельности позволяет по новому подойти к анализу причин аварийности на воздушном транспорте, что повысит профилактическую работу по снижению аварийности на воздушном транспорте.

Не нашли, что искали? Воспользуйтесь поиском: