
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Определение радиального маршрута доставки грузов
Со склада, на котором хранится груз (ОАО «Осколснаб», ст. Котел, промузел, площадка Складская, пр-д М-3, 3) в соответствии с индивидуальным вариантом курсового проекта, необходимо распределить часть груза (3 тонны) по магазинам Старого Оскола. При этом необходимо определить оптимальный маршрут движения транспортного средства. В качестве критерия оптимальности использовать минимум пройденного расстояния.
1. Определите возможные адреса поставки в зависимости от специфики груза, данные представьте в табл. 5 (в качестве объема поставки использовать указанные в табл. 5 показатели).
Таблица 5
Адреса магазинов в Старом Осколе
| Наименование | Адрес | Объем поставки, кг | |
| … | |||
| …. | |||
| …. | |||
| …. | |||
| Итого |
2. Определите матрицу расстояний между магазинами и складом, на котором хранится груз, результаты представьте в табл. 6
Здесь рассмотрен пример для развоза товара по 5 магазинам. В работе необходимо выбрать 6 магазинов. Предполагается, что не между всеми парами объектов существует проезд. В курсовом проекте необходимо рассмотреть расстояния между всеми возможными парами объектов, тогда, табл. 6 будет заполнена полностью.
Для поиска информации о расстояниях внутри городов можно воспользоваться ресурсом: http://maps.google.ru/.
Необходимо определить порядок развозки грузов по магазинам, стоимость перевозки, и время доставки, если средняя скорость передвижения по городу составляет 23 км/час, а время на разгрузку в каждой точке маршрута – 0,5 часа.
Таблица 6
Пример заполненной матрицы расстояний
| Склад | Магазин 1 | Магазин 2 | Магазин 3 | Магазин 4 | Магазин 5 | |
| Склад | - | 3,7 | ||||
| Магазин 1 | - | 6,2 | 8,2 | - | ||
| Магазин 2 | 6,2 | 2,5 | 4,3 | - | ||
| Магазин 3 | 2,5 | 2,5 | 1,5 | |||
| Магазин 4 | 3,7 | 8,2 | 4,3 | 2,5 | - | |
| Магазин 5 | - | - | 1,5 | - |
Постановка задачи:
Заданы пункты потребления (табл. 5). Груз необходимо развести из начального пункта (склада) во все остальные пункты (потребители). Потребность (объем поставки) указана в табл. 5. На складе имеется транспортное средство грузоподъемностью 3 т. Известно расстояние между потребителями (табл. 6). Схема размещения пунктов и расстояния между ними приведены на рис. 1

Рис. 1. Пример схемы размещения потребителей
Этап 1. Строим кратчайший путь, связывающий все пункты без замкнутых контуров (рис. 2).

Рис. 2. Кратчайший путь
Этап 2. Определяем рациональный порядок объезда пунктов маршрута. Для этого строим матрицу (табл. 7), в которой по диагонали размещаем пункты маршрута (обратите внимание: пункты маршрута указываются в порядке кратчайшего пути на рис. 2), а в соответствующих клетках – кратчайшие расстояния между пунктами (в соответствии с рис. 1). Для примера матрица является симметричной, однако в курсовом проекте она может получиться несимметричной. Это связано с различными способами проезда по улицам города.
Таблица 7
Пример матрицы кратчайших расстояний, км
| Номер | Склад | 2,0 | 3,0 | 5,5 | 3,7 | 11,9 |
| 2,0 | Магазин 5 | 1,5 | 4,0 | 5,7 | 10,2 | |
| 3,0 | 1,5 | Магазин 3 | 2,5 | 6,7 | 8,7 | |
| 5,5 | 4,0 | 2,5 | Магазин 2 | 4,3 | 6,2 | |
| 3,7 | 5,7 | 6,7 | 4,3 | Магазин 4 | 8,2 | |
| 11,9 | 10,2 | 8,7 | 6,2 | 8,2 | Магазин 1 | |
| Итого | 26,1 | 23,4 | 22,4 | 22,5 | 28,6 | 45,2 |
Начальный маршрут строим для трех пунктов матрицы, имеющих наибольшие размеры сумм, показанных в строке «Итого», т.е. Магазин 1 – Магазин 4 – Склад.
Для включения последующих пунктов берем следующий по убыванию суммы пункт – Магазин 5 и решаем между какими пунктами его включить:
- Магазин 1 – Магазин 4;
- Магазин 4 – Склад;
- Склад – Магазин 1.
Чтобы это решить для каждой пары пунктов необходимо найти размер приращения маршрута по формуле

где i – индекс включаемого пункта; k – индекс первого пункта из пары; p – индекс второго пункта из пары; Сki – расстояние между k -м и i -м пунктами, км.; Сiз – расстояние между i -м и p -м пунктами, км.
При включении пункта – Магазин 5 (м5) между Магазин 1 (м1) и Магазин 4 (м4) определяем размер приращения:


Аналогично определяем приращения между парами м4 – с (склад) и с – м1.
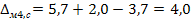

Из полученных значений необходимо выбрать минимальное.
Таким образом, получилась последовательность:
Магазин 1 – Магазин 4 – Склад – Магазин 5
Используя этот метод и формулу определяем между какими пунктами расположить Магазин 2 (м2) и Магазин 3 (м3).
Добавление Магазина 2:


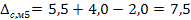

Маршрут: Магазин 1 – Магазин 4 – Склад – Магазин 5 – Магазин 2
Добавление Магазина 3:





Маршрут: Магазин 1 – Магазин 4 – Склад – Магазин 5 – Магазин 3 – Магазин 2
Любой маршрут должен начинаться и заканчиваться на складе, поэтому ответом будет маршрут, представленный на рис. 3.

Рис. 3. Разработанный маршрут
Не нашли, что искали? Воспользуйтесь поиском: