
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Определение рациональных маятниковых маршрутов
Оставшиеся грузы необходимо распределить по складской сети Старого Оскола в соответствии с индивидуальным заданием. Потребности каждого склада представить в табл. 8 (общая потребность – 12 т, является одинаковой для всех вариантов).
Таблица 9
Информация по складской сети
| Наименование (индивидуальное задание) | Адрес (индивидуальное задание) | Объем поставки, т | |
| Итого: |
Необходимо определить рациональные маятниковые маршруты доставки потребителям, если известно:
Грузоподъемность одного транспортного средства составляет 1,5 т.
Время работы на маршруте – 9 часов в день.
Время на погрузку, разгрузку и оформление документов – 1 час.
Средняя скорость движения – 25 км/час.
Далее необходимо выбрать автотранспортное предприятие, которое будет осуществлять перевозку. Адрес автотранспортного предприятия определить самостоятельно
Далее представлен пример расчета параметров маршрута. В табл. 9 представлены исходные данные для примера. При расчете учтено, что объем развозимого груза составляет 12 т.
Таблица 9
Пример исходных данных
| Пункт отправления | Пункт назначения | Объем перевозок, т | Объем перевозок за одну поездку, т | Количество поездок |
| Склад временного хранения | С1 | 1,5 | ||
| С2 | 1,5 | |||
| С3 | 1,5 | |||
| С4 | 1,5 | |||
| С5 | 1,5 | |||
| Итого |
Этап 1. Определите расстояния между объектами логистической сети. Результаты удобно свести в табл. 10.
Таблица 10
Пример матрицы расстояний до складов, км
| Исходный пункт | Пункт назначения | ||||||
| АТП (А) | Склад (С) | С1 | С2 | С3 | С4 | С5 | |
| Автоколонна | - | ||||||
| Склад | - |
Этап 2. Необходимо определить затраты времени на одну поездку (пример в табл.11).
Для расчета затрат времени необходимо использовать формулу
 ,
,
где tc-i-c – время работы на маршруте, мин; с – индекс склада; i – индекс потребителя; lc-i – расстояние между складом и потребителем, км; li-c – расстояние между потребителем и складом, км; t пр – время, необходимое на погрузку и разгрузку, мин; V – скорость транспортного средства, км/час.
Аналогично рассчитывается время работы на маршруте, при условии возвращения в автоколонну
 ,
,
где tc-i-a – время работы на маршруте, мин; с – индекс склада; i – индекс потребителя; a – индекс автоколонны; lc-i – расстояние между складом и потребителем, км.; li-a – расстояние между потребителем и автоколонной, км.; t пр – время, необходимое на погрузку и разгрузку, мин; V – скорость транспортного средства, км/час.
Пример расчета для маршрута: Склад железнодорожной станции (далее Склад) – Склад 1
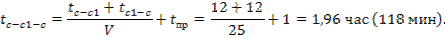
Результат представить в табл. 11
Таблица 11
Пример расчета затрат времени на одну поездку
| Маршрут | Затраты времени, мин |
| Склад – С1 – Склад | |
| Склад – С1 – Автоколонна | |
| Склад – С2 – Склад | |
| Склад – С2 – Автоколонна | |
| Склад – С3 – Склад | |
| Склад – С3 – Автоколонна | |
| Склад – С4 – Склад | |
| Склад – С4 – Автоколонна | |
| Склад – С5 – Склад | |
| Склад – С5 – Автоколонна |
В табл. 11 строка маршрута «Склад – С1 – Склад» – означает, что транспортное средство загружается товаром на складе железнодорожной станции, едет до Склада 1, разгружается, а после этого возвращается обратно для последующей загрузки.
Строка маршрута «Склад – С1 – Автоколонна» означает, что транспортное средство загружается товаром на складе предприятия, едет до Склада 1, разгружается, а после этого возвращается в Автоколонну и больше в этот день не возит товар.
Этап 3. Составляем исходную рабочую матрицу (табл. 12).
Таблица 12
Пример исходной матрицы
| Пункт назначения | Расстояние до автоколонны, км | Расстояние до склада, км | Разность расстояния, км | Количество необходимых поездок |
| С1 | 6 (18-12) | |||
| С2 | ||||
| С3 | -4 | |||
| С4 | ||||
| С5 |
Наименьшую оценку (-4) имеет пункт назначения Склад 3, а наибольшую оценку (11) Склад 2. Это означает, что начальным пунктом маршрута будет Склад 2, и весь рабочий день транспортное средство будет отвозить грузы в этот склад и лишь последняя поездка будет на Склад 3, откуда автомобиль поедет в автоколонну. Это необходимо для минимизации порожнего пробега.
Маршрут номер 1 для одного автомобиля: Автоколонна – Склад – Склад 2 – Склад – Склад 3 – Автоколонна. Известно, что время работы на маршруте составляет 9 часов в день (540 мин). Если автомобиль обслужит Склад 3 и вернется оттуда в автоколонну, он затратит 108 мин (табл. 12). Следовательно, на обслуживание Склада 2 остается 432 мин (540-108).
Если время на поездку на Склад 2 и обратно составляют 74 мин, то в этот пункт автомобиль сможет сделать 5 поездок. Но по условиям задачи необходимо лишь 4.
Таким образом, маршрут этого транспортного средства на рабочий день включает 4 поездки на Склад 2 и одну на Склад 3 (результаты представлены в табл. 17).
Этап 4. Определяем новую исходную матрицу (табл.13).
Таблица 13
Исходная матрица
| Пункт назначения | Расстояние до автоколонны, км | Расстояние до склада, км | Разность расстояния, км | Количество необходимых поездок |
| С1 | ||||
| С3 | -4 | |||
| С4 | ||||
| С5 |
Наибольшую оценку разности расстояния имеет Склад 1, а наименьшую Склад 3.
Маршрут номер 2 для одного автомобиля: Автоколонна – Склад – Склад 1 – Склад – Склад 3 – Автоколонна. Известно, что время работы на маршруте составляет 9 часов в день (540 мин). Если автомобиль обслужит Склад 3 и вернется оттуда в автоколонну, он затратит 108 мин. Следовательно, на обслуживание Склада 1 остается 432 мин (540-108).
Если время на поездку на Склад 1 и обратно составляют 118 мин, то в этот пункт автомобиль сможет сделать 4 поездки. Полученный маршрут представлен в табл. 17
Этап 5. Определяем новую исходную матрицу (табл. 14).
Таблица 14
Исходная матрица
| Пункт назначения | Расстояние до автоколонны, км | Расстояние до склада, км | Разность расстояния, км | Количество необходимых поездок |
| С3 | -4 | |||
| С4 | ||||
| С5 |
Наибольшую оценку разности расстояния имеет Склад 5, а наименьшую Склад 3.
Маршрут номер 3 для одного автомобиля: Автоколонна – Склад – Склад 5 – Склад – Склад 3 – Автоколонна. Известно, что время работы на маршруте составляет 9 часов в день (540 мин). Если автомобиль обслужит Склад 3 и вернется оттуда в автоколонну, он затратит 108 мин. Следовательно, на обслуживание Склада 1 остается 432 мин.
Если время на поездку на Склад 5 и обратно составляют 146 мин, то в этот пункт автомобиль сможет сделать 2 поездки. После двух поездок останется еще 140 минут. Это позволит совершить еще одну поездку в пункт 4.
Полученный маршрут представлен в табл. 17
Этап 6. Определяем новую исходную матрицу (табл. 15)
Наибольшую оценку разности расстояния имеет Склад 4, а наименьшую Склад 3.
Таблица 15
Исходная матрица
| Пункт назначения | Расстояние до автоколонны, км | Расстояние до склада, км | Разность расстояния, км | Количество необходимых поездок |
| С3 | -4 | |||
| С4 |
Маршрут номер 4 для одного автомобиля: Автоколонна – Склад – Склад 4 – Склад – Склад 3 – Автоколонна. Известно, что время работы на маршруте составляет 9 часов в день (540 мин). Если автомобиль обслужит Склад 3 и вернется оттуда в автоколонну, он затратит 108 мин. Следовательно, на обслуживание Склада 4 остается 432 мин. Это позволит автомобилю сделать 3 поездки.
Полученный маршрут представлен в табл. 17
Этап 7. Определяем новую исходную матрицу (табл. 16).
Таблица 16
Исходная матрица
| Пункт назначения | Расстояние до автоколонны, км | Расстояние до склада, км | Разность расстояния, км | Количество необходимых поездок |
| С3 | -4 | |||
| С4 |
Наибольшую оценку разности расстояния имеет Склад 4, а наименьшую Склад 3.
Маршрут номер 5 для одного автомобиля: Автоколонна – Склад – Склад 4 – Склад – Склад 3 – Автоколонна.
Полученный маршрут представлен в табл. 17
Таблица 17
Сводная маршрутная ведомость
| № | Маршрут | Показатели маршрута | ||||
| Количество поездок | Объем перевозок, т | Количество автомобилей, шт. | Время работы, мин | |||
| Склад – Склад 2 - Склад | 5,0 | |||||
| Склад – Склад 3 - Автоколонна | 1,5 | |||||
| Итого | 6,5 | |||||
| Склад – Склад 1 - Склад | 6,0 | |||||
| Склад – Склад 3 - Автоколонна | 1,5 | |||||
| Итого | 7,5 | |||||
| Склад – Склад 5 - Склад | 3,0 | |||||
| Склад – Склад 4 – Склад | 1,5 | |||||
| Склад – Склад 3 - Автоколонна | 1,5 | |||||
| Итого | 6,0 | |||||
| Склад – Склад 4 – Склад | 4,5 | |||||
| Склад – Склад 3 - Автоколонна | 1,5 | |||||
| Итого | 6,0 | |||||
| Склад – Склад 4 – Склад | 1,0 | |||||
| Склад – Склад 3 – Склад | 4,5 | |||||
| Склад – Склад 3 – Автоколонна | 1,5 | |||||
| Итого | 7,0 | |||||
| Итого |
3. 3. Распределение потребителей по складской сети
В ходе работы над курсовым проектом грузы были распределены между складами (табл. 8). Далее необходимо прикрепить выбранные вами магазины к складам, для организации дальнейших поставок. Всего в течение месяца будет необходимо развести по магазинам 12 т. грузов (табл.18).
Объем поставки в каждый магазин определяется самостоятельно.
Таблица 18
Адреса магазинов Старого Оскола
| Наименование | Адрес | Объем поставки, т | |
| Данные о магазинах берутся из табл. 5 | |||
Прикрепление потребителей (магазинов) к складам осуществляется с применением методов линейного программирования.
Рассмотрим пример решения задачи. Имеется 5 поставщиков (склады логистической сети), располагающих определенным количеством продукции (табл. 8), и 5 потребителей (магазины), у которых есть потребность в данной продукции 57 т.
Необходимо определить транспортные затраты на доставку груза от любого поставщика до любого потребителя и прикрепить потребителей так, чтобы суммарные транспортные расходы по доставке продукции поставщикам были минимальными.
Этап 1. Определяем транспортные затраты. Затраты на транспортировку зависят от расстояния от склада до потребителя. Стоимость перевозки одной тонны груза на один километр составляет 50 руб/т. Предположим, что расстояние от Склада 1 до Магазина 1 составляет 24 км, тогда стоимость доставки одной тонны груза составит 1200 руб.
Информацию о расстояниях необходимо определить самостоятельно, используя ресурс http://maps.google.ru/. Результаты расчета стоимости доставки груза представить в виде табл. 19.
Для построения экономико-математической модели введем обозначения: i – номер поставщика (i = 1,…, m), m – количество поставщиков (в курсовом – 5); j - номер потребителя (j = 1,…, n), n – количество поставщиков (в курсовом – 5); Ai – ресурсы i -го поставщика, т.е. количество груза, которое поставщик может поставить потребителям (табл.9), т; Вj – потребность в продукции j -го потребителя (табл. 19), т; Cij – транспортные расходы по доставке одной тонны груза от i -го поставщика j -му потребителю, руб./т.; Xij – количество продукции, поставляемой от i -го поставщика j -му потребителю, т. Эта величина неизвестна и подлежит определению.
Таблица 19
Транспортные расходы по доставке одной тонны груза от i -го поставщика j -му потребителю
| Потребитель Поставщик | Магазин 1 | Магазин 2 | Магазин 3 | Магазин 4 | Магазин 5 |
| Склад 1 | |||||
| Склад 2 | |||||
| Склад 3 | |||||
| Склад 4 | |||||
| Склад 5 |
Экономико-математическая модель должна содержать целевую функцию, системы ограничений и условия неотрицательности переменных. В рассматриваемой задаче необходимо свести к минимуму транспортные расходы

где Cij – транспортные расходы по доставке одной тонны груза от i -го поставщика j -му потребителю, руб./т.; Xij – количество продукции, поставляемой от i -го поставщика j -му потребителю, т.
Достижение минимального значения целевой функции происходит при определенных условиях (ограничениях). Первое из них состоит в том, что по оптимальному варианту от каждого поставщика планировалось то количество продукции, которым он располагает
 .
.
Второе заключается в том, что по оптимальному плану количество продукции каждому потребителю должно соответствовать его потребности
 .
.
Наконец, в модели указывается условие не отрицательности переменных
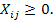
После построения модели решается задача прикрепления поставщиков потребителям. Расчеты могут выполняться методом потенциалов (табл. 20). В этой таблице кроме ресурсов поставщиков, потребностей потребителей и транспортных расходов, имеются столбец и строка для записи потенциалов Ui и Vj, которые дают возможность определить оптимальность плана закрепления поставщиков за потребителями. В правом верхнем углу ячеек указана стоимость доставки продукции (руб/т).
Этап 1. Составление исходного плана. Для составления исходного плана воспользуемся приемом, который называется «метод северо-западного угла». Согласно этому методу заполнение таблицы следует начинать с левого верхнего квадрата и с позиции этого квадрата сравнить ресурсы первого поставщика (15 т) и потребности первого потребителя (6 т), выбрать меньшее из них и записать в данный квадрат, которые теперь называется «загруженным» (табл. 22). Это означает, что потребности первого потребителя удовлетворены. Затем необходимо подвинуться вправо и сравнить оставшиеся у первого поставщика ресурсы (15 – 6 = 9) и потребность второго потребителя (16), записав меньшую цифру в ячейку первой строки второго столбца, передвинуться вниз, т.к. ресурсы первого поставщика закончились, а потребность второго потребителя еще не удовлетворена. Так, двигаясь шаг за шагом, получаем исходный план.
Таблица 20
Исходные данные
| Потребители | М1 | М2 | М3 | М4 | М5 | Ресурсы поставщиков Ai, т | ||||||
| Поставщик | Vj Ui | V1 | V2 | V3 | V4 | V5 | ||||||
| C1 | U1 | X11 | X12 | X13 | X14 | X15 | ||||||
| C2 | U2 | X21 | X22 | X23 | X24 | X25 | ||||||
| C3 | U3 | X31 | X32 | X33 | X34 | X35 | ||||||
| C4 | U4 | X41 | X42 | X43 | X44 | X45 | ||||||
| C5 | U5 | X51 | X52 | X53 | X54 | X55 | ||||||
| Потребность Bj, т |
Таблица 21
Исходный план прикрепления потребителей к поставщикам
| Потребители | М1 | М2 | М3 | М4 | М5 | Ресурсы поставщиков Ai, т | ||||||
| Поставщик | Vj Ui | |||||||||||
| C1 | ||||||||||||
| C2 | ||||||||||||
| C3 | ||||||||||||
| C4 | ||||||||||||
| C5 | ||||||||||||
| Потребность Bj, т |
Этап 2. Проверка исходного плана. Необходимо проверить исходный план на соответствие следующим условиям:
Число «загруженных» клеток в таблице должно быть на единицу меньше суммы чисел поставщиков и потребителей, в рассматриваемом примере 9 (5 + 5 – 1), т.е. условие соблюдено.
Не должно быть ни одного занятого квадрата, который оказался бы единственным в строке и столбце таблицы, т.е. условие соблюдено.
Этап 3. Проверка на оптимальность. Для осуществления проверки исходного плана на оптимальность необходимо рассчитать потенциалы Ui и Vj. Эти потенциалы определяются только для «загруженных» ячеек. Сумма индексов Ui и Vj должна быть равна транспортным издержкам соответствующих ячеек. В этом примере U1 + V1 = 1200; U1 + V2 = 1300; U2 + V2 = 1600; U3 + V2 = 900; U3 + V3 = 850; U4 + V3 = 1300; U4 + V4 = 1700; U5 + V4 = 2100; U5 + V5 = 2200.
Индексы определяем следующим образом:
1) принимаем U1 = 0 (так всегда);
2) из первого уравнения получаем V1 = 1200 – 0 = 1200;
3) из второго уравнения получаем V2 = 1300 – 0 = 1300;
4) точно также, решая все уравнения, определяем потенциалы для всех потребителей и поставщиков (табл. 22).
Далее для «незагруженных» ячеек рассчитывается  (в табл. 22 рассчитанные значения представлены курсивом).
(в табл. 22 рассчитанные значения представлены курсивом).
Полученные значения  , как правило, отличаются от значений Cij (транспортные расходы). Если во всех «незагруженных» ячейках соблюдается неравенство
, как правило, отличаются от значений Cij (транспортные расходы). Если во всех «незагруженных» ячейках соблюдается неравенство  , то план считается оптимальным. В рассматриваемом примере есть ячейки, в которых это неравенство не соблюдается, а значит, план не является оптимальным.
, то план считается оптимальным. В рассматриваемом примере есть ячейки, в которых это неравенство не соблюдается, а значит, план не является оптимальным.
Таблица 22
Исходный план прикрепления потребителей к поставщикам с рассчитанными значениями потенциалов
| Потребители | М1 | М2 | М3 | М4 | М5 | Ресурсы поставщиков Ai, т | ||||||
| Поставщик | Vj Ui | |||||||||||
| C1 | 1250 | 1650 | 1750 | |||||||||
| C2 | 1500 | 1550 | 1950 | 2050 | ||||||||
| C3 | - 400 | 800 | 1250 | 1350 | ||||||||
| C4 | 1250 | 1350 | 1700 | |||||||||
| C5 | 1650 | 1750 | 1700 | |||||||||
| Потребность Bj, т |
Этап 4. Улучшение исходного плана. Это происходит путем перемещения поставки в «незагруженную» ячейку, в которой  В нашем примере это квадрат С2-М3 (1550 – 500 = 1050). В случае если разность окажется одинаковой для нескольких ячеек, следует выбрать любую ячейку произвольно.
В нашем примере это квадрат С2-М3 (1550 – 500 = 1050). В случае если разность окажется одинаковой для нескольких ячеек, следует выбрать любую ячейку произвольно.
Итак, в рассматриваемом примере поставка должна быть перемещена в квадрат С2-М3. Перемещения производятся в определенном порядке с тем, чтобы не были нарушены условия, выраженные в приведенных выше уравнениях. Для этого образуем связку, т.е. замкнутую ломаную линию, состоящую из вертикальных и горизонтальных отрезков, таким образом, чтобы одной из вершин образованного многоугольника был квадрат, куда производится перемещение, а остальные вершины находились в «загруженных ячейках». В табл. 23 представлен такой многоугольник.
После образования связи свободному квадрату и связанным с ним «загруженным» ячейкам присваиваются поочередно знаки «+» и «–», начиная со свободного квадрата.
Таблица 23
Перемещение поставки в квадрат С2-М3
| Потребители | М1 | М2 | М3 | М4 | М5 | Ресурсы поставщиков Ai, т | ||||||
| Поставщик | Vj Ui | |||||||||||
| C1 | 1250 | 1650 | 1750 | |||||||||
| C2 | 1500 | 1550 | 1950 | 2050 | ||||||||
| C3 | - 400 | 800 | 1250 | 1350 | ||||||||
| C4 | 1250 | 1350 | 1700 | |||||||||
| C5 | 1650 | 1750 | 1700 | |||||||||
| Потребность Bj, т |
Среди тех квадратов, которые отмечены знаком «–», выбираем наименьший объем поставки (6 т.). Именно этот объем подлежит перемещению из квадратов со знаком «–» в квадраты со знаком «+». В результате получен новый план (табл. 24).
Таблица 24
Скорректированный план прикрепления потребителей к поставщикам
| Потребители | М1 | М2 | М3 | М4 | М5 | Ресурсы поставщиков, Ai, т | ||||||
| Поставщик | Vj Ui | |||||||||||
| C1 | ||||||||||||
| C2 | ||||||||||||
| C3 | ||||||||||||
| C4 | ||||||||||||
| C5 | ||||||||||||
| Потребность Bj, т |
Повторяем описанные выше шаги. Результат представлен в табл. 25
Таблица 25
План прикрепления потребителей к поставщикам с рассчитанными значениями потенциалов
| Потребители | М1 | М2 | М3 | М4 | М5 | Ресурсы поставщиков Ai, т | ||||||
| Поставщик | Vj Ui | |||||||||||
      C1 C1
| 1250 | 1200 | 1300 | |||||||||
| C2 | - 750 | 450 | 550 | 450 | 550 | |||||||
     C3 C3
| - 400 | 800 | 800 | 900 | ||||||||
     C4 C4
| 1250 | 1350 | 1350 | |||||||||
    C5 C5
| 2100 | 2200 | 2250 | |||||||||
| Потребность Bj, т |
Это решение также не является оптимальным, следовательно, необходимо его улучшить путем перенесения поставок в свободные ячейки (в ячейку С5-М1). Результат представлен в табл. 27
Таблица 27
Скорректированный исходный план прикрепления потребителей к поставщикам
| Потребители | М1 | М2 | М3 | М4 | М5 | Ресурсы поставщиков Ai, т | ||||||
| Поставщик | Vj Ui | |||||||||||
| C1 | ||||||||||||
| C2 | ||||||||||||
| C3 | ||||||||||||
| C4 | ||||||||||||
| C5 | ||||||||||||
| Потребность Bj, т |
Проверим его на оптимальность (табл. 28).
Таблица 28
План прикрепления потребителей к поставщикам с рассчитанными значениями потенциалов
| Потребители | М1 | М2 | М3 | М4 | М5 | Ресурсы поставщиков Ai, т | ||||||
| Поставщик | Vj Ui | |||||||||||
| C1 | 1250 | 1650 | 2750 | |||||||||
| C2 | -750 | 450 | 550 | 900 | 2000 | |||||||
| C3 | - 400 | 800 | 1250 | 2350 | ||||||||
| C4 | 1250 | 1350 | 2800 | |||||||||
| C5 | - 500 | 800 | 750 | 1150 | ||||||||
| Потребность Bj, т |
Полученное решение является оптимальным, так как для всех ячеек соблюдается неравенство  .
.
Не нашли, что искали? Воспользуйтесь поиском: