АНАЛИЗ УСТОЙЧИВОСТИ САУ ЧАСТОТНЫМИ МЕТОДАМИ

Цель работы

Изучение и приобретение практических навыков применения критерия Найквиста и метода ЛЧХ для анализа устойчивости САУ.

3.1. Основные сведения

Процессы управления в линейных разомкнутых САУ описываются уравнениями вида:

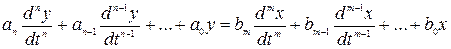, (3.1)

Общее решение однородного уравнения

имеет вид , , где 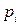являются корнями характеристического уравнения

(3.2)

и определяют устойчивость системы, т.е. способность возвращаться в установившееся состояние после прекращения действия, которое вывело её из этого состояния.

Система является устойчивой, если все корни располагаются в левой полуплоскости комплексной переменной, т.е. являются отрицательными или имеют отрицательные вещественные части. Для определения устойчивости используются различные критерии, позволяющие определять знаки корней без их вычисления.

Наибольшее применение нашли частотные критерии устойчивости, а среди них критерий Найквиста и метод ЛЧХ, основанные на принципе аргумента. При переходе в частотную область анализа заменой 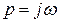, изменение аргумента каждого сомножителя в уравнении (3.2) при определяется в среднем следующим выражением:

,

где знак "+" соответствует корню 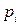левой, а "-" – правой полуплоскости (рис. 3.1).

Рис. 3.1. Изменение аргумента для корней

левой и правой полуплоскости

Если характеристическое уравнение имеет корней в правой и в левой полуплоскости, то

при .

Для устойчивой разомкнутой системы и принцип аргумента с учетом симметрии определяется выражением

при .

Анализ устойчивости замкнутых САУ основывается на применении принципа аргумента к выражению

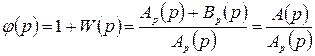, (3.3)

где - передаточная функция разомкнутой системы, - характеристический полином замкнутой системы.

Согласно данному принципу изменение аргумента определяется выражением

при .

При наличии корней в характеристическом уравнении замкнутой системы, расположенных в правой полуплоскости комплексной переменной, и при условии устойчивости разомкнутой системы справедливо равенство

при .

Отсюда очевидно, что для систем, устойчивых в разомкнутом и замкнутом состояниях, выполняется условие критерия Найквиста

при .

Графическая интерпретация этого условия для статической системы показана на рис. 3.2,а.

Переход к АФХ САУ, т.е. к её комплексному коэффициенту передачи, полученному из (3.3) по выражению

,

дает возможность сформулировать критерий Найквиста следующим образом.

САУ, устойчивая в разомкнутом состоянии, устойчива в замкнутом состоянии в том и только в том случае, если АФХ разомкнутой системы, построенная при , не охватывает критическую точку с координатами (рис. 3.2,б).

Рис 3.2. Критерий устойчивости Найквиста: а – в плоскости ; б – в плоскости ; 1 – устойчивая САУ; 2 – неустойчивая САУ

Следует отметить, что при АФХ астатических систем претерпевает разрыв. При этом 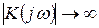, а фаза меняется на , где - порядок астатизма, за счет того, что нулевой корень относят к левой полуплоскости (рис. 3.3,а), т.е. производят замену , где , а меняется от до .

Следовательно, для интегратора справедливо выражение

,

объясняющее вид его АФХ, приведенный на рис. 3.3,б.

Критерий Найквиста, интерпретированный в область ЛЧХ, получил название метода ЛЧХ. Согласно этому методу САУ, устойчивая в разомкнутом состоянии в том и только в том случае, когда на частоте среза разомкнутой системы, т.е. частоте, при которой , , фазовый сдвиг не превосходит значения .

Рис. 3.3. АФХ интегратора: а – в плоскости ; б – в плоскости

Применение метода ЛЧХ к анализу устойчивости астатической системы первого порядка показано на рис. 3.4. На этом же рисунке показано определение запасов устойчивости по фазе и по модулю .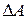

Рис. 3.4. Интерпретация критерия Найквиста в области ЛЧХ:

а – устойчивая астатическая система первого порядка; б – метод ЛЧХ

3.2. Порядок выполнения работы

Перед началом работы следует получить у преподавателя номер варианта параметров исследуемых САУ.

1. Анализ устойчивости статической системы

а) Определение устойчивости методом ЛЧХ

Создайте структуру замкнутой системы с единичной обратной связью, на вход которой подается единичное ступенчатое воздействие, а передаточная функция прямой цепи соответствует заданной передаточной функции разомкнутой системы. Задайте требуемые значения параметров.

Получите ЛЧХ исследуемой системы, подобрав диапазон изменения частоты таким образом, чтобы в него входили все сопрягающие частоты.

На полученной ЛАХ постройте асимптотическую ЛАХ, определите частоту среза и фазовый сдвиг на этой частоте.

Сделайте вывод об устойчивости исследуемой системы. Для устойчивой системы определите запасы устойчивости по фазе и модулю .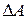

б) Определение устойчивости по критерию Найквиста

Получите качественный вид АФХ, исследуемой системы при изменении частоты от верхней границы выбранного диапазона частот до минимально необходимого значения.

Путем изменения нижней границы частоты найдите критическую точку на мнимой оси и напечатайте АФХ исследуемой системы вблизи этой точки.

По полученной АФХ определите фазовый сдвиг на частоте среза.

Сделайте вывод об устойчивости исследуемой системы. Для устойчивой системы определите запасы устойчивости по фазе и по модулю. Сравните результаты с п. 1,а.

в) Проверка устойчивости методом моделирования

Проведите имитационное моделирование. Получите график переходной функции, подобрав экспериментально время моделирования, исходя из возможности вывода об устойчивости исследуемой системы. Напечатайте график.

2. Анализ устойчивости астатической системы первого порядка

Выполните операции п. 1.

3. Анализ устойчивости астатической системы второго порядка

Выполните операции п. 1.

3.3. Варианты заданий

В данной работе применяются критерий Найквиста и метод ЛЧХ для анализа устойчивости статических и астатических систем первого и второго порядка.

Передаточные функции исследуемых систем в общем виде определяются следующим образом:

.

Исходные данные для моделирования указанных систем приведены в табл. 3.1.

Таблица 3.1

3.4. Содержание отчета по работе

1. Цель работы.

2. Структурные динамические схемы исследованных систем, их передаточные функции с числовыми значениями параметров и экспериментально полученные графики АФХ, ЛЧХ и переходных функций.

3. Ответы на контрольные вопросы.

3.5. Контрольные вопросы

1. На каком принципе основан частотный критерий устойчивости Найквиста?

2. Как формулируется критерий устойчивости Найквиста?

3. Чему равны координаты критической точки?

4. В чем особенность построения АФХ для астатических систем?

5. Чему равен фазовый сдвиг вблизи нулевой частоты для статических и астатических систем?

6. К чему стремится АФХ статических и астатических систем при бесконечно большом увеличении частоты ?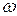

7. Как определяются запасы по фазе и модулю с помощью АФХ исследуемой системы?

8. Как определяются запасы по фазе и модулю с помощью ЛЧХ исследуемой системы?

9. В чем заключается связь между АФХ и ЛЧХ САУ?

Не нашли, что искали? Воспользуйтесь поиском: