
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ЛАБОРАТОРНАЯ РАБОТА № 6
ИССЛЕДОВАНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
С ЗАПАЗДЫВАНИЕМ
Цель работы
Определение влияния величины запаздывания на устойчивость систем управления на основе структурных преобразований исследуемой системы в зависимости от места нахождения звена с запаздыванием.
6.1. Основные сведения
Системы с запаздыванием отличаются от обычных линейных САУ отличием одного или нескольких звеньев, величина на выходе которых  начинает меняться при изменении величины на входе
начинает меняться при изменении величины на входе 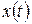 с некоторой постоянной временной задержкой
с некоторой постоянной временной задержкой  , т.е.
, т.е.  .
.
Подобные звенья с "чистым" запаздыванием имеют передаточную функцию вида
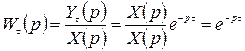 ,
,
которой соответствует комплексный коэффициент передачи
 ,
,
а частотные характеристик определяются выражениями
 ,
,  ,
,  .
.
 ,
,  .
.
Таким образом, АФХ звена с запаздыванием представляет собой круг единичного радиуса на комплексной плоскости  с центром в начале координат, ЛАХ имеет нулевое значение и инвариантна к изменениям частоты, а ЛФХ неограниченно убывает с увеличением частоты.
с центром в начале координат, ЛАХ имеет нулевое значение и инвариантна к изменениям частоты, а ЛФХ неограниченно убывает с увеличением частоты.
При последовательном включении звена с запаздыванием вместе с обычными динамическими звеньями передаточная функция и комплексный коэффициент передачи разомкнутой системы будут
 ,
, 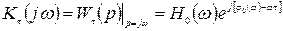 , (6.1)
, (6.1)
где  ,
,  ,
, 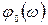 - соответственно передаточная функция, амплитудная и фазовая частотные характеристики разомкнутой системы без учета запаздывания.
- соответственно передаточная функция, амплитудная и фазовая частотные характеристики разомкнутой системы без учета запаздывания.
Следовательно, системы, отличающиеся друг от друга лишь величиной запаздывания, имеют одинаковые амплитудные и различные фазовые характеристики. При этом большей величине запаздывания  соответствует больший фазовый сдвиг на частоте среза системы, что приводит к ухудшению её устойчивости.
соответствует больший фазовый сдвиг на частоте среза системы, что приводит к ухудшению её устойчивости.
Устойчивость системы с запаздыванием определяется с помощью критерия Найквиста по передаточной функции и комплексному коэффициенту передачи исследуемой системы в виде (6.1). Это требует структурных преобразований исходной системы в зависимости от места нахождения звеньев с запаздыванием.
Так, если данное звено включено в прямую цепь, то при размыкании главной обратной связи (см. рис. 6.1,а)
 ,
,
где  - коэффициент передачи звена с запаздыванием.
- коэффициент передачи звена с запаздыванием.
Если же звено запаздывания включено в местную обратную связь, то (см. рис. 6.1,б)
 ,
,

Рис. 6.1. АФХ (а) и ЛЧХ (б) САУ: 1 -  ; 2 -
; 2 -  ; 3 -
; 3 - 
что соответствует размыканию местной обратной связи.
Формулировка критерия Найквиста для систем с запаздыванием меняется. Однако в рассматриваемых системах явления устойчивости и неустойчивости чередуются при непрерывном изменении  .
.
Для определения условий устойчивости вводится понятие критического времени запаздывания  , которое определяется из равенства фазовой частотной характеристики разомкнутой системы на частоте среза
, которое определяется из равенства фазовой частотной характеристики разомкнутой системы на частоте среза 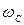 величине
величине  , т.е. (см. рис. 6.2)
, т.е. (см. рис. 6.2)
 .
.
Отсюда определяем
 , (6.2)
, (6.2)
где 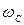 определяется из условия
определяется из условия 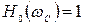 .
.

Рис. 6.2. Структурные преобразования исследуемой системы
с размыканием главной (а) и местной (б) обратной цепи
6.2. Порядок выполнения работы
Перед началом работы следует получить у преподавателя номер варианта параметров исследуемой САУ (табл. 6.1).
1. Определение критического времени запаздывания
а) В Simulink создайте структуру, соответствующую рис. 6.2,а при  , т.е. при отсутствии звена с запаздыванием. Задайте требуемые значения параметров.
, т.е. при отсутствии звена с запаздыванием. Задайте требуемые значения параметров.
б) Проведите имитационное моделирование, подобрав время решения исходя из полученного на экране графика переходного процесса. Напечатайте его.
в) Получите и напечатайте ЛЧХ и АФХ исследуемой разомкнутой структуры, по которой определите частоту среза и запас по фазе на этой частоте. При этом график АФХ напечатайте вблизи критической точки.
г) По выражению (6.2) рассчитайте критическое время запаздывания.
д) Определите критическое время запаздывания аналитическим путём, используя экспериментально полученное значение 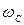 . Сравните результаты.
. Сравните результаты.
2. Определение временных и частотных характеристик исследуемой САУ при наличии звена с запаздыванием в прямой цепи
а) Введите звено с запаздыванием в исследуемую структуру в соответствии с рис. 6.2,а.
б) Изменяя значение  при
при  , подберите такое его значение, при котором визуально наблюдается заметное изменение переходной функции. Нанесите на полученный в п. 1,б график новые значения переходной функции в узловых точках. Постройте график.
, подберите такое его значение, при котором визуально наблюдается заметное изменение переходной функции. Нанесите на полученный в п. 1,б график новые значения переходной функции в узловых точках. Постройте график.
в) Нанесите на полученные в п. 1,в в характеристики новые значения частотных характеристик. Постройте графики.
г) Выполните п. "б" и "в" для  .
.
д) Выполните п. "б" и "в" для 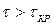 .
.
3. Определение временных и частотных характеристик исследуемой САУ при наличии звена с запаздыванием в цепи местной обратной связи
Выполните п. 1 и п. 2 для структуры, изображенной на рис. 6.2,б.
6.3. Варианты заданий
В данной работе исследуется влияние величины запаздывания на устойчивость системы управления при наличии в ней звена с запаздыванием как в прямой цепи, так и в цепи местной обратной связи.
При этом исходная разомкнутая система без запаздывания представляет собой последовательное соединение двух апериодических звеньев, т.е. имеет передаточную функцию
 .
.
Исходные данные для моделирования данной передаточной функции приведены в табл. 6.1.
Таблица 6.1

6.4. Содержание отчета по работе
1. Цель работы.
2. Схемы исследованных систем, их передаточные функции с числовыми значениями параметров, экспериментально полученные графики и результаты аналитических расчетов.
3. Ответы на контрольные вопросы.
6.5. Контрольные вопросы
1. Чем отличаются системы с запаздыванием от обычных линейных систем?
2. Какова зависимость выходной величины звена с "чистым" запаздыванием от его входной величины?
3. Как записывается передаточная функция звена с запаздыванием?
4. Какой вид имеют частотные характеристики звена с запаздыванием?
5. Каково влияние запаздывания на ЛЧХ исследуемой САУ?
6. Каково влияние запаздывания на АФХ исследуемой САУ?
7. С помощью какого критерия определяется устойчивость систем с запаздыванием?
8. Зависит ли устойчивость САУ от расположения звена запаздывания в исследуемой структуре?
9. Что называется критическим временем запаздывания?
10. Как определяется критическое время запаздывания?
СПИСОК ЛИТЕРАТУРЫ
1. Бесекерский В. А., Попов Е. П. Теория систем автоматического управления. – СПб.: Изд-во "Профессия", 2003. – 752 с.
2. Воронов А. А. Основы теории автоматического управления. – М.: Высшая школа. – Часть I. – 1986.
3. Дьяконов В. Simulink 4. Специальный справочник. – СПб: Питер, 2002.
4. Епишкин А. Е. Исследование динамических процессов в системе MATLAB – Simulink. Методические указания. СПб., 2004. – 32 с.
5. Первозванский А. А. Курс теории автоматического управления. – М.: Наука, 1986. – 616 с.
6. Цыпкин Я. З. Основы теории автоматических систем. – М.: Наука, 1977. – 559 с.
Не нашли, что искали? Воспользуйтесь поиском: