Закон Ома для участка цепи

Напряжение на участке цепи. Под напряжением на некотором участке электрической цепи по­нимают разность потенциалов между крайними точками этого участка.

На рис.2.1 изображен участок цепи, крайние точки которого обоз­начены буквами а и b. В соответствии с определением напряжения между точками а и b:

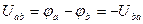(2.1)

Положительное направление напряжения на каком-либо участке цепи (направление отсчёта этого напряжения), указываемое на рисунках стрел­кой, совпадает с положительным направлением отсчёта тока, протекающего по данному участку цепи (рис.2.1).

Закон Ома для участка цепи, не содержащего э.д.с. Пусть ток (рис.2.1) I течет от точки а к точке b (от более высокого потенциала к более низкому). Следовательно, потенциал точки а выше потенциала точки b на величину, равную про­изведению тока I на сопротивление R:

или

(2.2)

, далее

или

,

откуда ток:

(2.3)

Для рис.2.2, б поменяется знак при э.д.с. Е:

. (2.3^/)

В общем виде можно записать:

. (2.4)

Уравнение (2.4) математически выражает закон Ома для участка цепи, содержащего э.д.с.; знак «плюс» перед Е соответствует согласованному её направлению с током (рис.2.2, а), знак «минус» — встречному (рис.2.2, б).

Законы Кирхгофа

Все электрические цепи подчиняются первому и второму законам Кирхгофа.

Первый закон Кирхгофа можно сформулировать двояко:

1) алгебраическая сумма токов, подтекающих к любому узлу схемы, равна нулю;

2) сумма подтекающих к любому узлу токов равна сумме утекаю­щих от узла токов.

На рис.2.3. показан узел схемы с входящими и выходящими из него токами. Будем считать выходящие токи со знаком «плюс», а входящие со знаком «минус» (возможно принять и наоборот). Тогда согласно первой формулировке:

,

согласно второй —

.

Очевидно, что эти два выражения не противоречат друг другу.

Ток в каждом из сопротивлений определяется по закону Ома:

Ток в источнике по первому закону Кирхгофа равен сумме всех токов:

или

.

Выражение в скобках представляет собой эквивалентную проводимость

. (2.5)

Второй закон Кирхгофа также можно сформулиро­вать двояко:

1) алгебраическая сумма падений напряжения в любом замкнутом контуре равняется алгебраической сумме э.д.с. вдоль того же контура:

.

В каждую из сумм соответствующие слагаемые входят со знаком «плюс», если они совпадают с направлением обхода контура, и со зна­ком «минус», если они не совпадают с ним. Для левого контура схемы рис.2.5:

.

2) алгебраическая сумма напряжений (не падений напряжения!) вдоль любого замкнутого контура равна нулю:

.

Так, для периферийного контура схемы рис.2.5:

.

Напряжение на каждом из сопротивлений определяется по закону Ома:

.

Напряжение на источнике по второму закону Кирхгофа равно сумме падений напряжения

или

.

Выражение в скобках представляет собой эквивалентное сопротивление

. (2.6)

Не нашли, что искали? Воспользуйтесь поиском: