Для оценки работоспособности объекта

Задание условий работоспособности в форме ограничений на перемещение полюсов и нулей передаточной функции позволяет упорядочить показатели, характеризующие состояние объекта по степени их влияния на положение полюсов и нулей передаточной функции на комплексной плоскости.

Пусть состояние объекта характеризуется n непосредственно измеримыми показателями

.

Представим характеристическое уравнение объекта, являющееся его диагностической моделью в виде

. (2.11)

Определим векторы относительных чувствительностей для случая простых корней и для случая кратных корней.

Для случая простых корней компоненты вектора чувствительностей могут быть рассчитаны по формуле:

; k = 1,2,...,n; p=0,1,2,...,n–1;(2.12)
а для случая кратных корней:

; q=1,...,k; p=0,...,n–1; (2.13)

Упорядочение показателей осуществляется по нормам векторов

или (2.14)

При этом считается, что l_p ³ l_m, если для случая простых корней и для случая кратных корней.

Проведя такое упорядочение показателей, можно выбрать такую минимальную совокупность показателей, которая обеспечивает наилучшую (при данном числе показателей) достоверность оценки действительного состояния объекта.

Рассмотрим следующий пример.

Пусть вектор параметров, характеризующих состояние объекта, представлен тремя параметрами

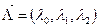, а характеристическое уравнение объекта приведено к виду

,

причём a₀(l₀) = 0.4 + l₀; a₁(l₁) = 1.7 + l₁; a₂(l₂) = 2.3 + l₂.

В исходном состоянии, т.е. при l₀ = l₁= l₂ = 0 , характеристическое уравнение примет вид

.

Получили действительное кубическое уравнение. Для нахождения его корней можно использовать метод Кар дано. Для этого вводится подстановка x=y–a₂/3, где a₂ – коэффициент при x², получаем

y³ + py + q = 0,

где , ,
где a₁ – коэффициент при x₁, а a₀ – свободный член. Подставляя значения a₂, a₁, a₀, получим

Подставляя значения коэффициентов p и q, получаем “неполное” кубическое уравнение:

y³ – 0.63y – 0.02 = 0

Его корни равны

y₁ = A+B, ,

где , , .

Проведём необходимые вычисления

Q=(–0.063/3)³ + (–0.02/2)² = –0.926×10^–5 + 10⁴ = 9×10^–5 = 0.9×10^–4

y₁ = 0.27 + 0.0794 = 0.306

y₃ = –0.153 – 0.165 = –0.138

x₁ = y₁ – 2.3/3 = 0.306 – 0.766 = –0.46

x₂ = 0.012 – 0.766 = –0.754

x₃ = –0.318 – 0.766 = –1.085

Теперь можно определить относительные чувствительности корней T_l = (t_1p, t_2p, t_3p), воспользовавшись формулой (2.12):

,

, ,

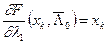Подставляя теперь вместо x_k значения корней, получаем:

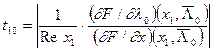
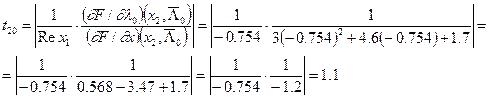
Теперь рассчитаем нормы векторов чувствительностей

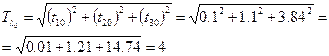
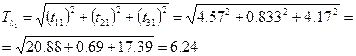
Таким образом, самым чувствительным является параметр l₁, затем идёт l₂, а потом l₀, хотя все они оказались близкими по чувствительности.

Следует учитывать, что при эксплуатации объекта соотношение между чувствительностями различных показателей может измениться. Например, вследствие временных изменений параметров могут измениться резонансные частоты объекта и, если в качестве контролируемых параметров были взяты выходные сигналы на определённых частотах при определённом входном воздействии, то соотношения чувствительностей этих параметров к состоянию объекта, выражающемуся условиями работоспособности, изменятся.

Не нашли, что искали? Воспользуйтесь поиском: