Методы определения работоспособности объекта

Работоспособность объекта определяется его состоянием. Для оценки же состояния объекта необходимо заставить его или выполнять свои рабочие функции, или подавать на его входы специальные “тестовые” воздействия. В первом случае будет осуществляться так называемая “проверка функционирования”, а во втором – оценка объекта по специально измеряемым параметрам или характеристикам.

При проверках на функционирование, как правило, отсутствует количественная оценка, т.е. результат такой проверки выражается дуальным суждением – “ да ” – “ нет ”.

Во втором случае в качестве контролируемых параметров объекта могут рассматриваться параметры его отдельных элементов, коэффициенты передаточной функции, параметры динамических звеньев объекта и т.д. В качестве контролируемых характеристик могут сопоставляться статические или динамические характеристики диагностируемого и эталонного объектов или их отдельные показатели, такие как передаточный коэффициент (коэффициент усиления), время нарастания или спада выходного сигнала в ответ на скачкообразное входное воздействие, время достижения заданного уровня, период и число колебаний и др. Частотные характеристики могут сравниваться по максимальной амплитуде в полосе пропускания, частотам среза, крутизне среза, ширине полосы пропускания и т.п.

Если в самом общем случае в качестве диагностической модели использовать передаточную функцию, которая в общем случае имеет вид

K(p) = (a_npⁿ + a_n-1p^n-1 + … + a₀)/ (b_mp^m + b_m-1p^m-1 + … + b₀), (2.17)

причём n<m

то её можно разложить в цепную дробь:

(2.18)

При этом частные передаточные функции: K₁(p), K₂(p), K₃(p) и т.д. определяются в результате деления полиномов знаменателя на полиномы числителя

(2.19)

Каждая частная модель K₁(p), K₂(p) и т.д. может рассматриваться как приближённая модель, а её погрешность из–за отбрасывания остатка в разложении (2.18) может быть оценена на каждом шаге разложения с помощью выражений:

;

; (2.20)

и т.д.

Рассмотрим пример. Пусть объект описывается передаточной функцией

.

Разложим передаточную функцию в цепную дробь, сделав три шага, и оценим погрешность разложения на каждом шаге.

Прежде всего преобразуем передаточную функцию к полиномиальному виду

Проведём операции деления полиномов в соответствии с (2.19)

Таким образом разложение имеет вид

Подставляя p=jw, определим погрешности:

1) на первом шаге

.

Для нахождения модуля этой погрешности умножим и разделим это выражение на (16–8jw–w²)

, откуда

и по фазе

2) на втором шаге

.

Соответственно, её модуль будет

,

а погрешность по фазе

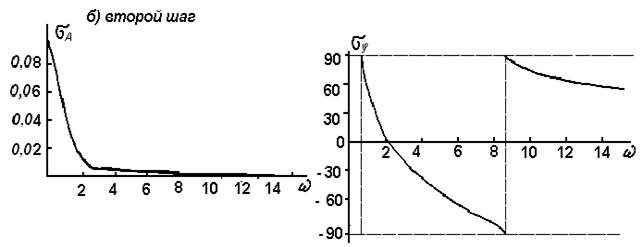
На третьем шаге выражения для погрешностей получаются ещё более громоздкими, поэтому мы их приводить не будем, а для сопоставления величин погрешностей на первом, втором и третьем шагах приведем графики их зависимостей от w (рис. 2.3).

Рис. 2.3. Зависимость погрешностей s_А и s_j от частоты при разложении передаточной функции в цепную дробь (s_А модуль погрешности, s_j - погрешность по фазе

Эквивалентная диагностическая модель объекта может быть получена не только из передаточной функции путем ее разложения в цепную дробь, но и по его динамическим характеристикам путем их аппроксимации аналитической функцией с заданной степенью точности.

Например, любую временную функцию на конечном отрезке времени от нуля до Т можно аппроксимировать конечным рядом вида

, 0£t£T (2.21)

где f_i(t) – аналитические функции, a_i – постоянные коэффициенты, которые подбираются с использованием критерия минимума дисперсии методом наименьших квадратов.

Можно строить эквивалентные диагностические и по частотным характеристикам объекта. Причем для этого достаточно аппроксимировать аналитическими функциями только амплитудно-частотную характеристику объекта, т.к. эквивалентность АЧХ в большинстве случаях определяет и эквивалентность фазовых характеристик.

Если для получения диагностической модели использованы временные характеристики, то для оценки работоспособности объекта целесообразно использовать интегральные показатели. Для этого можно рекомендовать функции вида

(2.22)

где F_i(t) – координаты, характеризующие состояние объекта.

При выборе вида функционала для осуществления интегральной оценки должны соблюдаться требования зависимости J от всех величин, характеризующих состояние объекта.

В частности для получения линейных интегральных оценок можно использовать выражения вида

, i=0, 1, 2,..., n, j=0, 1, 2,..., m (2.23)

при этом y(t)=h(¥) – h(t),

где h(¥) и h(t) –значения контролируемой временной характеристики при t=¥ и текущем значении.

Эти оценки могут быть применены только при апериодичности аппроксимируемых временных характеристиках.

При колебательном характере временной характеристики используются квадратичные интегральные оценки вида

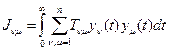(2.24)
где T_nm – заданные коэффициенты.

Если объект характеризуется одной величиной y(t) и ее производными, то интегральная квадратичная оценка будет иметь вид

(2.25)
где k=0, 1, 2,..., n, i=0 при j=0, i=1 при j=1, 2,..., n k=1, 2,..., n представляют собой сумму интегралов от квадрата производных функции y(t):

(2.26)
причем каждое из слагаемых можно использовать как самостоятельную интегральную оценку. Однако для практики достаточно ограничиться первыми тремя слагаемыми J₀, и , поскольку все следующие слагаемые оказываются очень малыми.

При выборе тех или иных интегральных оценок для определения работоспособности конкретных объектов следует учитывать их чувствительность к изменению величин, характеризующих состояние объекта.

В качестве примера рассмотрим объект, структурная схема которого представлена на рис. 2.4.

x(t)

К_у К₁/p y(t)

К_ос(Т_осp+1)

Рис. 2.4. Структурная схема объекта

В качестве интегральной оценки его работоспособности примем

(2.27)
где y_ном(t), y(t) – временные зависимости выходной величины y эталонного и диагностируемого объекта. Из структурной схемы следует, что состояние объекта характеризуется тремя величинами: К_у, К_ос и Т_ос.

Экспериментально полученные зависимости указанной интегральной оценки при отклонениях каждого из параметров К_у, К_ос и Т_ос от номинальных значений в диапазоне от 0 до ±100% представлены на рис. 2.5. А на рис. 2.6. и 2.7. показаны временные зависимости эталонного и диагностируемого объекта при фиксированных отклонениях только одного параметра К_у (в одном случае К_у=0.2К_{у ном} в другом К_у=2К_{у ном}). Из рис. 2.5. видно, что чувствительность интегральной оценки к изменениям параметров К_у и К_ос почти одинаковая, но сильно отличается к изменению параметра Т_ос

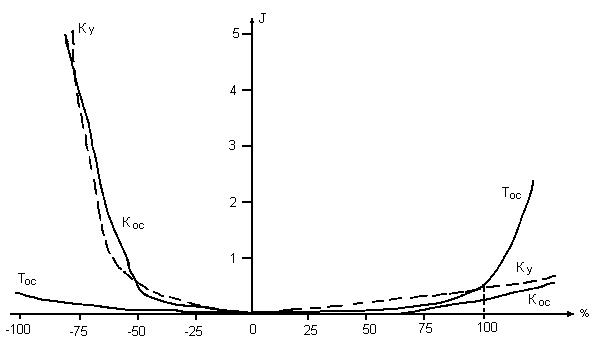
Рис. 2.5. Зависимость интегральной оценки работоспособности объекта от отклонений параметров объекта К_у, К_ос и Т_ос от номинальных значений

Не нашли, что искали? Воспользуйтесь поиском: