
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Статистические модели накопления повреждений
При построении статистических моделей накопления повреждений рассматривается следующая физическая ситуация [ ]: изделие функционирует циклически во внешней среде; во время циклов происходят необратимые изменения; они аккумулируются до тех пор, пока это изделие уже не может удовлетворительно функционировать, то есть наступает отказ изделия. Момент времени, при котором происходит отказ - время до отказа или время жизни изделия. Процесс накопления необратимых изменений называют процессом кумулятивных повреждений, к которому могут быть отнесены: усталостный износ, рост усталостных трещин, ползучесть и т.п.
Для построения модели кумулятивных повреждений используется теория цепей Маркова. Эти модели объединяют основные источники разброса, встречающиеся в физических процессах кумулятивных повреждений. Для введения цепей Маркова рассматривается последовательность исходов эксперимента {Е1,Е2,...,Ет}, где Еj (j=1,2,...,n) - взаимоисключающие исходы, образующие полную группу событий. Результат эксперимента (событие Еj) есть некоторое состояние процесса.
Данный подход может быть формализован в виде графа состояний, которому соответствует матрица переходов. Например, графам, представленным на рисунке 3.4, соответствуют матрицы переходов (ненулевой элемент отмечен знаком «+»):
 (4.15)
(4.15)
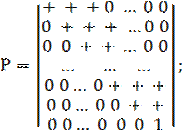 (4.16)
(4.16)
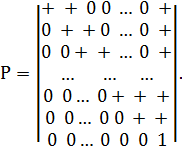 (4.17)
(4.17)
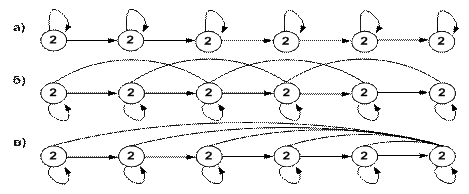
Рис. 4.4. Графы переходов, соответствующие: а-матрице
переходов (4.15); б - матрице переходов (4.16); в - матрице переходов (4.17)
Для построения физически интерпретируемых распределений для процессов кумулятивных повреждений было предложено использовать модель удара [ ]. В этих моделях и время, и состояния повреждения дискретны (в отличие от других, в которых может быть время непрерывно, а состояния процесса дискретны). Предполагается, что цикл нагружения - это повторяющийся период функционирования изделия, в течение которого могут накапливаться повреждения; время фиксируется в виде количества циклов нагружения (например, обороты вала, включение и отключение некоторого устройства, возвратно-поступательное движение ползуна и т.п.). Предполагается, что существует некоторое состояние b, достижение которого фиксируется как отказ. При х = 0 повреждение находится в состоянии 1, и в период цикла нагружения происходит удар. Если сила удара ниже некоторого критического уровня, то повреждение не возникает. В противном случае возникает единичное повреждение. Вероятность того, что сила удара ниже критического уровня р1 , a q1 = 1 - р1 - вероятность того, что сила удара выше критического уровня. Далее принимается, что до момента первого выхода удара за критический уровень реализуется последовательность независимых испытаний - схема Бернулли, для которой характерна независимость испытаний (q1 - вероятность успеха в одном испытании). Повреждение находится при х = 0 в состоянии 1 и остается в нем до момента первого выброса удара за критический уровень, после чего повреждение переходит в состояние 2. Вероятности р1 и q1 не зависят от х, но эта зависимость может возникнуть. Время до момента первого выброса подчиняется геометрическому распределению (следствие схемы Бернулли). Аналогично процесс повторяется в состоянии 2 и т.д. Таким путем процесс накопления повреждения «подрастает» на единицу до тех пор, пока не будет достигнуто состояние b (состояние отказа).
В случае, когда рj и qj =l - рj при j = 1,2,...,b-1 не зависят от х (времени), модель является стационарной; в противном случае - нестационарной. Если pj и qj зависят от j, тогда модель процесса зависит от состояний; в противном случае (pj = const, qj = const для j = 1,2,...,6-1) - не зависит. Предположение о том, развитие процесса (история) полностью определяется его настоящим состоянием, является свойством марковости.
В простейшем случае, когда цикл нагружения имеет постоянную жесткость, матрица переходных вероятностей имеет вид
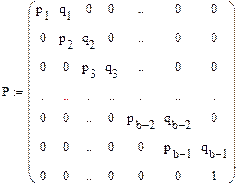
(4.18)
Вид матрицы говорит о том, что реально можно рассмотреть не слишком большое число шагов j, а также о том, что так называемое (формально введенное подобие физического процесса, например, возникновение повреждения при ударе) единичное накапливающееся повреждение физического смысла не имеет. Даже если рассматривать рост единичной трещины (наращивание ее длины после определенного случайного числа циклов нагружения), то от такой модели (трудоемкой с инженерной точки зрения) для решения практических задач помощи недостаточно.
По нашему мнению, процесс накопления повреждений необходимо строить статистически с самого начала, что будет продемонстрировано в следующих главах.
Предложены обобщения простейшей модели. Для этого вводится жесткость цикла нагружения, уменьшающаяся во времени, и в связи с этим принимается, что функция qj(k) имеет следующий вид:
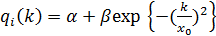 (4.19)
(4.19)
где k - номер цикла нагружения, то есть время, измеряемое числом циклов; параметр у может принимать значения  0 (
0 (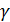 > 1 и
> 1 и 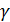 < 1).
< 1).
Если жесткость цикла нагружения увеличивается во времени, эта же функция принимается в виде
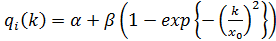 (4.20)
(4.20)
Выбор этих функций не обосновывается; это означает, что критерием вида этих функций, а также значений входящих в них параметров является совпадение с данными эксперимента.
Таким образом, теоретическая обоснованность предложенных и рассмотренных в [ ] моделей остается проблематичной. Это можно проиллюстрировать выводом распределения Вейбулла. Авторы [ ] получают формулы для нестационарного процесса Пуассона, следуя [ ], и называют процессом Вейбулла. Модификация процесса Пуассона строится следующим образом: исключается положение о том, что число событий на временном интервале зависит только от длины этого интервала, но не зависит от его положения на оси времени, откуда следует, что
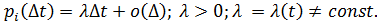 (4.21)
(4.21)
Затем интенсивность потока событий задается выражением
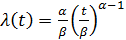 (4.22)
(4.22)
Однако следует заметить, что вид l(t) в выражении (4.22) есть следствие того, что функция распределения есть функция распределения Вейбулла, но никак не наоборот. Вейбулла же строил распределение, названное его именем, как эмпирическое. Поэтому, строго говоря, распределение, построенное подобным образом, следует так же, как и распределение Вейбулла, считать эмпирическим. Таким образом, результаты той обработки экспериментальных данных, которые представлены в [ ], есть не более чем иллюстрация того, что продемонстрировал Вейбулл [ ]: для механических систем и их отказов (в случае, например, усталостного разрушения) наиболее приемлемым является распределение, названное его именем, которое подробно рассматривается в следующих главах. Следует также отметить, что, в отличие от распределения, принимаемого в [ ], распределение Вейбулла предполагает наличие параметра сдвига, физический смысл которого в рамках эмпирических закономерностей не поддается объяснению (это отмечал и Вейбулл). Тем не менее этот параметр должен быть введен для адекватного представления данных эксперимента.
Не нашли, что искали? Воспользуйтесь поиском: