Логический контроль

Логические методы контроля состоят в проверке искусственно соз­данных контрольных соотношений, причем эти соотношения мало связаны с существом информации, которая подлежит пересылке, хранению или пе­реработке. Логический контроль находит широкое применение в различ­ных устройствах хранения и передачи данных, а также ЭВМ. Зачастую для реализации этого метода контроля в устройства вводятся дополнительные узлы: сумматоры, элементы сравнения и т. д.

Рассмотрим разновидности логического контроля, нашедшие приме­нение в практике.

Контрольное суммирование. Отдельным неизменяющимся масси­вам кодовых слов (программам, исходным данным, результатам и т. д.) ставятся в соответствие избыточные контрольные слова (эталонные слова), которые заблаговременно получают путем суммирования всех слов данно­го массива. Для осуществления контроля производится суммирование всех слов массива, и полученный результат поразрядно сравнивают с эталон­ным словом. Их совпадение с высокой вероятностью гарантирует, что в проверяемом массиве слов искажения отсутствуют.

Контрольное суммирование реализуется достаточно просто, эффек­тивно и широко используется на практике.

Чаще всего оно применяется в следующих случаях:

1) для контроля правильности хранения информации в различных
видах памяти. При этом производится периодическое суммирование слов
контролируемых массивов, и полученная контрольная сумма сравнивается
с эталонной;

2) для контроля правильности пересылки информации между различными устройствами. В этом случае по мере пересылки отдельных слов массива осуществляется их суммирование, в результате чего получается
контрольная сумма, которая поразрядно сравнивается с эталоном, пересы-лаемым в последнюю очередь;

3) при первоначальном вводе массивов слов в отдельные устройства В этом случае ввод информации производится дважды, каждый раз с контрольным суммированием. Если обе контрольные суммы совпали, то считают, что ввод произведен верно, а контрольная сумма принимается за эталонную.

Суммирование может производиться либо по программе, либо при помощи специального сумматора. Наиболее распространенными способа­ми контрольного суммирования являются следующие:

• поразрядное суммирование слов по модулю 2;

• арифметическое суммирование слов без кольцевого переноса в
младший разряд;

• арифметическое суммирование с кольцевым переносом из стар-шего в младший разряд (суммирование по модулю 2"', где т - длина слов).

Первый способ имеет наименьшую эффективность, последний -наибольшую. Второй способ занимает промежуточное положение.

При очень малых вероятностях искажений значений разрядов эффективность контроля при различных методах суммирования будет почти одинакова. В случае относительно больших значений вероятности q суммирование по модулю 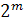обеспечивает большую вероятность обнаруже­ния ошибок.

Проверка переменной на появление запрещенных комбинаций. Суть проверки состоит в сравнении какой-либо переменной x с заранее из­вестными разрешенными или запрещенными значениями пе­ременных, причем X .

При нормальной работе x X, а при наличии ошибок x X У.

Контроль может проводиться следующими двумя способами.

Первый способ состоит в проверке попадания переменной x в мно­жество X разрешенных значений. При этом проверяются условия x = . Если для одного из г равенство соблюдается, то считают, что ошибка от­сутствует.

Второй способ состоит в проверке попадания переменной x в множе­ство Y запрещенных значений. При этом проверяются условия x = 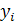. Если

для всех j неравенство соблюдается, то также считают, что ошибка отсут­ствует.

В каждом конкретном случае необходимо выбрать такой способ, ко­торый обеспечивал бы минимальное число проверок. Покажем на примере, как можно применить этот метод контроля для устройств, работающих с десятичными двоично-кодированными числами.

В таблице 6.1 представлены множества допустимых и запрещенных слов для одной тетрады. Поскольку запрещенных наборов меньше, то в данном случае целесообразно организовать контроль вторым способом, т. е. проверять условия x = (j=1,2, 3, 4, 5, 6). Практически контроль

реализуется при помощи циклического выполнения команды поразрядного сравнения, причем контролируемая переменная сравнивается со словами, в каждой тетраде которых записаны запрещенные слова.

Данный метод контроля не обладает высокой эффективностью и, как правило, требует введения большого числа дополнительных команд и за­трат времени для своего осуществления. Его целесообразно применять, ко­гда имеется острая потребность в контроле, а другие способы использовать нельзя. Можно, например, рекомендовать проверку запрещенных комби­наций для контроля передачи типовых сообщений по линиям связи от або­нентов в вычислительную машину. В сообщении, как правило, содержится слово-признак, определяющее смысловой состав переданного сообщения.

Слова-признаки имеют малое число допустимых значений, их иска­жения приводят к очень грубым нарушениям работы программ, а контроль правильности приема этих слов другими способами осуществить трудно.

Таблица 6.1

Допустимые слова	Запрещенные слова

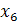
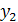
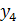
Многократное хранение информации. Один и тот же массив ин­формации (программы, исходные данные, константы и т. д.) дублируется и записывается в нескольких местах оперативной или внешней памяти.

Контроль состоит в том, что периодически либо непосредственно перед использованием дублированные массивы сличаются между собой. Этот метод контроля практически обнаруживает все искажения, возникшие по­сле размножения массива. Недостаток метода состоит в существенном увеличении объема памяти и большом времени осуществления контроля.

Приведем примеры использования многократного хранения инфор­мации. Программа устранения последствий сбоя может быть дублирована и дважды записана в оперативной памяти. Перед исправлением ошибки, возникшей в результате появления сбоя, целесообразно сличить обе про­граммы и лишь затем включить одну из них в работу.

В качестве другого примера можно привести многократное хранение программы-диспетчера (супервизора). Известно, что эта программа организует вычислительный процесс в многопрограммных и многопроцессорных вычислительных машинах. Ее разрушение приводит к полной потере работоспособности машины. Поэтому программа-диспетчер хранится в не­скольких экземплярах а оперативной и внешней памяти (дискетах, дисках). Периодически эти программы сличаются между собой. При искажениях программа-диспетчер должна быстро автоматически восстанавливаться, поэтому ее размножают в количестве не менее трех экземпляров.

Для повышения достоверности хранения информации во внешних запоминающих устройствах с движущимся носителем используют парал­лельную запись одних и тех же данных на нескольких дорожках. Это по­зволяет с высокой вероятностью обнаруживать ошибки в процессе считы­вания, а применение мажоритарных способов дает возможность осущест­вить также восстановление искаженной информации.

Контроль переменных на соответствие физическому смыслу. Этот вид контроля может быть использован, если переменные имеют оп­ределенный физический смысл. Сущность контроля заключается в выяв­лении особенностей данной переменной и проверке выполнения этих осо­бенностей.

Эффективность данного контроля существенно зависит от физиче­ского смысла переменной и может быть оценена только применительно к каждому конкретному случаю. Как правило, контроль на соответствие фи­зическому смыслу относительно прост, позволяет выявить грубые ошибки вычислений, и применение его не создает особых затруднений.

Приведем отдельные примеры, поясняющие существо контроля. Пусть имеется программа вычисления координат самолета по данным ра­диолокационной станции, и среди переменных в программе имеется высо­та H. Очевидно, в качестве контрольного соотношения можно использо­вать неравенство .

Другим примером может служить проверка величины давления воды на лопасти в программе, управляющей режимами работы гидрогенера­тора. Из физического существа задачи ясно, что давление не может быть

отрицательным и не может превышать некоторой максимальной величины . Контрольное соотношение в этом случае будет иметь вид

Одним из частных случаев рассмотренного метода контроля является контроль скорости изменения переменных. Он может быть применен для контроля переменных x_i имеющих некоторый физический смысл и яв­ляющихся непрерывными функциями времени (координаты движущегося объекта, температура и т. д.).

Существо контроля состоит в том, что находится скорость изменения переменной

и проверяется условие

Допустимые пределы изменения переменной и исходя из физических особенностей задачи.

Например, программа оперирует с величиной азимута движуще­гося объекта, имеющего максимально возможную скорость . При больших дальностях до объекта справедливо соотношение

где /) - дальность до объекта; 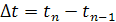-интервал времени измерения координат.

В качестве контрольного соотношения для скорости изменения ази­мута можно использовать соотношение

Могут быть найдены и другие более сложные соотношения. Логиче­ские методы контроля во многих случаях характеризуются высокой эф­фективностью. Они находят широкое применение на практике в цифровых вычислительных машинах, системах передачи данных и в различных видах памяти.

Не нашли, что искали? Воспользуйтесь поиском: