Алгоритмический контроль

Алгоритмические методы контроля, так же как и логические, преду­сматривают проверку контрольных соотношений. Однако сами контроль­ные соотношения непосредственно вытекают из математических особен­ностей решаемых задач. Алгоритмический контроль поэтому можно ис­пользовать только в устройствах, перерабатывающих информацию.

Каждая математическая задача имеет свои особенности, поэтому хо­тя бы относительно полное описание алгоритмических методов не пред­ставляется возможным.

Ниже будут рассмотрены отдельные наиболее типичные методы контроля. Каждый из них может быть использован для контроля правиль­ности решения определенного класса задач.

Проверка попадания в область ответа заключается в том, что для определенных этапов вычислений заблаговременно рассчитывается об­ласть возможных ответов при заданных ограничениях на значения исход­ных данных.

В программе после контролируемого участка необходимо преду­смотреть проверку попадания результата в область ответов. Если, напри­мер, область ответов результата у задана ( и ), то после вычисления необходимо осуществить проверку

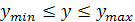
Приведем пример определения границ области ответа. Пусть требуется вычислить определенный интеграл

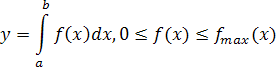
Область ответа в данном случае определяется соотношениями

В некоторых случаях границы области ответа не требуют вычисле­ний, так как они задаются самим существом получаемого результата. На­пример, если результатом вычислений является вероятность Р, то можно проверить удовлетворение условия

Если переменная у является синусом или косинусом, то можно про­верить условия

Проверка попадания в область ответа позволяет обнаружить грубые ошибки в реализации программ. Этот.метод контроля незначительно сни­жает коэффициент производительности и требует обычно небольшого числа дополнительных команд. Применение его целесообразно в тех слу­чаях, когда область ответа либо заранее известна, либо легко вычисляется.

Контроль методом обратного просчета состоит в том, что по полу­ченному результату находят исходные данные (аргументы) и сравнивают их с начальными исходными данными. Если они совпадают (с заданной точностью), то полученный результат считается верным. Для обратного просчета могут быть использованы обратные функции, например, и т. д.

Одним из примеров применения этого метода является контроль правильности вычисления кубического корня . Известно, что извле­чение кубического корня происходит по подпрограмме. Для контроля ра­боты этой подпрограммы можно возвести в куб результат и предусмотреть проверку условия 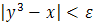Если указанное условие выполнено, то корень вычислен верно.

Обратный просчет позволяет с очень высокой вероятностью обнару­жения ошибок проконтролировать правильность выполнения программы. Преимущество его состоит еще и в том, что он одинаково эффективно об­наруживает ошибки, возникшие как в результате сбоев, так и в результате отказов.

Применение этого метода целесообразно в тех случаях, когда обрат­ный просчет не занимает много времени. В приведенном примере вычис­ление требует выполнения нескольких десятков команд, а проверка условия - всего пяти команд, следовательно, в данном случае метод обрат­ного просчета достаточно эффективен.

Проверка контрольных соотношений заключается в нахождении косвенных соотношений между переменными, участвующими в вычисле­ниях, и проверке соблюдения этих соотношений.

Например, если решается задача на вычисление углов А, В и С тре­угольника, то можно проверить соблюдение неравенств

Выполнение данного неравенства с высокой степенью вероятности гарантирует правильность выполнения программы.

Приведем еще один пример использования контрольных соотноше­ний.

Пусть имеется программа обращения матриц. Исходной матрицей является матрица . В результате выполнения программы получают обратную матрицу . Известно, что произведение прямой и обрат­ной матриц дает единичную матрицу. Следовательно, соотношени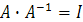е , где - единичная матрица, может быть использовано как кон­трольное. Его проверка обеспечивает выявление всех ошибок, вызванных как сбоями, так и отказами.

Недостатком данного соотношения является необходимость большо­го числа команд для его проверки. Можно получить более простые соот­ношения, требующие меньшего числа команд для своей реализации, но и обладающие меньшей эффективностью. Например, не производя полного умножения матриц А и , можно вычислить только отдельные элементы единичной матрицы и убедиться на выбор, что ее диагональные члены равны единице, а остальные - нулю.

Составим контрольные соотношения для проверки четырех элемен­тов единичной матрицы.

Обозначив , получаем

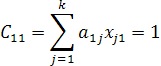
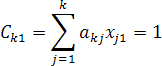
Отсюда находим контрольные соотношения

где е задается исходя из точности вычислений.

Проверка контрольных соотношений является эффективным мето­дом алгоритмического контроля. Рекомендуется применение этого метода во всех случаях, когда могут быть найдены относительно простые кон­трольные соотношения.

Проверка контрольных соотношений с использованием допол­нительных переменных состоит во введении искусственных переменных, которые либо связаны известными соотношениями основными переменными,

либо значения этих переменных при определенных условиях найде­ны заранее. По существу данный метод является одним из частных случаев метода проверки контрольных соотношений.

Можно выделить два случая введения дополнительных переменных. В первом случае вводятся математические переменные, не имеющие непо­средственного физического смысла, во втором - переменные, учитываю­щие физические особенности решаемой задачи. Дать какие-то общие ре­комендации по введению дополнительных переменных невозможно, так как здесь важна именно специфика задачи. Поэтому проиллюстрируем данный метод на примерах.

Пусть решается алгебраическое уравнение

Назовем это уравнение исходным, а корни его обозначим

Перейдем к новому уравнению

Корни этого вспомогательного уравнения обозначим . Первые п корней вспомогательного уравнения совпадают с корнями исходного, а последний n+1 корень равен а.

Теперь можно рекомендовать следующий способ контроля правиль­ности функционирования программы решения алгебраического уравнения:

перейти от исходного уравнения к решению вспомогатель­ного уравнения ;

найти все корни . вспомогательного уравнения;

для каждого полученного значения корня осуществить проверку

Если хотя бы для одного из корней неравенство выполняется, счита­ют, что уравнение решено верно. Здесь в качестве дополнительной пере­менной выступает заранее известное значение одного из корней.

Описанный метод может найти лишь ограниченное применение, так как в общем случае отыскиваются не все корни уравнения.

Покажем, как данный метод может быть применен для контроля ре­шения некоторых дифференциальных уравнений.

Допустим, что решается уравнение

при начальных условиях у(х_о)= у₀, у'(х_о)=у'₀.

Для контроля введем дополнительную переменную, продифферен­цировав дважды исходное уравнение:

Теперь, решая заданное уравнение, можно на каждом шаге (либо в выбранных точках) находить значения дополнительной переменной и про­верять условия

Выполнение этого неравенства будет свидетельствовать о правиль­ности вычислений. Два приведенных примера показывают, как можно ввести в про­грамму дополнительные переменные, непосредственно связанные с мате­матическими особенностями задачи.

Метод контроля за счет введения дополнительных переменных мож­но рекомендовать в тех случаях, когда для их реализации не требуется большого числа команд.

Контроль сравнением переменной с экстраполированным значе­нием используется, как правило, применительно к медленно меняющимся переменным. Состоит он в том, что на каждом шаге реализации програм­мы вычисляется два значения переменной. Одно значение вычисляется на основании вновь поступивших данных, другое (экстраполированное значение) находится исходя из значений переменных (), вы­численных на предыдущих шагах. В зависимости от обстоятельств могут применяться различные методы экстраполяции. На экстраполированное значение переменной накладывается так называемый строб Ах и находятся предельные возможные значения переменной и . Если значение попало внутрь строба, то считают, что ошибки вычислений отсутствуют, и программа продолжает выполняться обычным образом. Если же вычис­ленное значение переменной 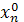вышло за пределы строба, то фиксируется факт наличия ошибки.

Приведем контрольные соотношения для линейного способа экстра­поляции:

Если величина постоянна, то строб называется фиксированным, если меняется в зависимости от некоторых условий, то строб носит на­звание динамического.

Программная реализация контроля с помощью фиксированного строба относительно проста, но обладает меньшей эффективностью, чем контроль с помощью динамического строба.

В простейшем случае для последующего определения величины ди­намического строба на каждом шаге реализации программы вычисляется

Величина 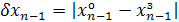. Величина строба для последующего шага нахо­дится из соотношения

где коэффициент к подбирается заблаговременно на основании тщательно­го изучения характера изменения переменной х.

Описанный метод контроля позволяет с высокой эффективностью проверять правильность вычисления медленно меняющихся переменных. Весьма положительным его качеством является то, что в определенной ме­ре он позволяет исключить влияние отдельных ошибок при работе про­граммы. Если, например, в результате ошибки значение вышло за пре­делы строба, то вместо можно взять величину и продолжать вычис­ления (в случае необходимости строб расширяют). Выход переменной за пределы строба на нескольких шагах подряд свидетельствует о грубых систематических ошибках в работе программы.

Подстановка результата применяется для контроля программ ре­шения линейных и нелинейных уравнений, а также систем уравнений.

Данный метод контроля состоит в том, что полученные результаты подставляются в исходное уравнение и проверяется, превратилось ли оно в тождество.

Пусть, например, программа предназначена для решения алгебраи­ческого уравнения вида

Получив в результате выполнения программы корни уравнения , можно подставить последовательно каждый из корней в уравнение и проверить выполнение неравенств

Величина г* при этом определяется заданной точностью вычислений. Если подстановка корня л:,- приводит к выполнению неравенства, то корень вычислен верно.

Данный метод обладает высокой эффективностью и его применение, как правило, бывает целесообразным.

Общих методов оценки эффективности алгоритмических методов контроля пока не существует. Поэтому в каждом конкретном случае необ­ходимо определять характеристики для выбранного метода, пользуясь приведенными выше соотношениями, и решать вопрос о целесообразности его применения.

Не нашли, что искали? Воспользуйтесь поиском: