Аныққан булар және сұйықтар 2 страница

7.52. Диаметірі d =1мм және d 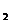=2мм өз ара қатынасқаг екі капиллярдың ішіндегі сынап деңгейлерінің айырмасын табу керек. Толық жұғады деп есептейміз.

7.53. Май шамның түбінен оның оттығына дейін (биіктігі h=10cм) керосин көтерілу үшін оның пілтесінің ұсақ тесігінің цилиндір сияқты түтік деп және толық жұғады деп есептейміз.

7.54. Ішкі диаметірі 2 мм капилляр сұиықтың ішінде батырылған. Капиллярдыңішімен көтерілген сұйықтың салмағы 9 10 кг-ға тең деп алып, сұйықтың беттік керілу коэффицентін табу керек.

7,55. Суы ыдыстың ішінде вертикаль етіп түсірілген капилляр түтікшенің ішкі радиусы r=0.16 мм, кең ыдыстың және капиллярдың ішіндегі судың деңгейі бірдей болу үшін, сұйықтың үстіндегі тұрған капиллярдың ішіндегі ауаның қысымы қандай болуы кереқ? Сыртқы қысым p =760 мм сын. бағ.-на тең. Сұйықты толық жұғады деп есептейміз.

7.56. Суы бар ыдыстың ішіне вертикаль етіп капилляр түтік түсірілген. Түтіктің жоғарғы жағы дәнекерленген. Түтіктің ішіндегі және кең ыдыстың ішіндегі судың деңгейі бірдей болуы үщін түтіктің ұзындығының 1,5 проценттей бөлігін судың ішіне батыруға тура келеді. Түтіктің ішкі радиусы неге тең? Сыртқы қысым 750 мм сын. бағ. тең. Сұйықты толық жұғады деп таламыз.

7.57. Сынаппен толтырылған барометірлік А түтікшенің ішкі d диаметірі: а) 5 мм б) 1,5 см-ге тең. Атмосфералық қысымды тікелей сынап бағанасының биіктігі бойынша табуға бола ма? Жоғарыдағы берілген әрбір жағдай үшін атмосфералық қысымды p =758 мм сын. бағ–на тең деп алып сынап бағынасының биіктігін табу керек. Сұйықты толық жұқпайды деп есептейміз.

7.58. Барометірлік түтіктің ішкі диаметірі 0,750см-ге тең. Атмосфералық қысымды чынап бағанасының биіктігі бойынша өлшей отырып қандай түзету енгізу керек. Сұйықты толық жұқпайды деп есептейміз.

7.59. Барометірлік түтіктің ішкі диаметірі 1)5 мм және 2) 10 мм-ге тең деп алып,сынап бағанасының биіктігі бойынша атмосфералық қысымды 760 мм сын. бағ-на деп есептегенде біздің жасайтын салыстырмалы қатеміз қандай болады.

7.60. Судың бетіне майланған (су толық жұқпаған жағдайда) болат ине тасталынған. Иненің әлш де батып кетпей судың бетіне тұруы үшін, оның ең үлкен диаметірі қандай болуы керек.

7.61. Диаметірі 1 мм майланған (су толық жұқпаған жағдайда) планита сымы бетіне жүзіп жүре ала ма?

7.62. Ішінде сынабы бар ыдыстың түбінде тесік бар. Сынап бағанасынығ биіктігі 3см-ге тең болғанда сынап ыдыстан ағып кетпеу үшін, тесіктің ең үлкен диаметірі қандай болуы керек.

7.63. Ауданы s=30см 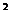шыны ыдыстың түбіне диаметірі d=0.5мм-ге тең тесіки бар. Ыдысқа сынап құйылған. Ыдыстың ішінде қалатын сынаптың мөлшері қанша.

7.64. Судың бетімен су инелігі деп алатын насеком жүгіріп жүреді. Инелектің алты табанының әрқайсысының астында радиусы 0,1 мм жарты сфера тәрізді шұңқыр пайда болады деп алып, су инелегінің салмағын табу керек.

7.65. Өлшемдері 9 х 12 см суланған екі фотопластинканы бір –бірінен (ығыстырмай) ажыратып алу үшін қандай күш жұмсау керек? Пластинкалардың арасындағы су қабатылың қалыңдығы 0,05 мм-ге тең. Толық жұғу деп аламыз.

7.66. Бір-бірінен 0,25 мм қашықтықта тұрған вертикал бағыттағы парпллель –жазық екі шыны пластинканың арасына су құйылған. Пластинканың арасындағы сұйықтың көтерілу биіктігі 3,1 см-ге ( һ30 дин/см) тең деп алып, сұйықтың тығыздығын табу керек. Толық жұқпайды деп аламыз.

7.67. Горизантал орналасқан параллел –жазық екі шыны пластинканың арасында 5г сынап орналасқан. Жоғарғы пластинканың үстіне 5кг жүк қойғанда, пластинкалардың ара қашықтығы 0,087 мм-ге тең болады. Жүктің салмағымен салыстырғанда, пластинканың салмағын есепке алмай, сынаптың беттік керілу коэффицентін табу керек. Толық жұқпайды депи есептейміз.

7.68. Ашық ткапиллярдың ішіне су тамшы бар. Капилярдың вертикаль қалыптағы жағдайында тамшы ұзындықтары: 1) 2 см 2) 4 см және 3) 2.98 см-ге тең су бағанасын жасайды. Капиллярдың ішкі диаметірі 1 мм–ге тең. Жоғарыда көрсетілген әрбір ұзындықтары үшін жоғарғы және төменгі менискілердің қисықтың радиусын табу керек. Толық жұғу деп есептейміз.

7.69.Ішкі диаметрі d=2 мм –ге тең горизанталь капиллярдың ішіне суды сорып кіргізгенде, ол су бағанасының ұзындығы h=10 см болады. Егер капиллярдың вертикаль қалыпта орналастырсақ,, онда қаншама су ағып шығады? Толық жұғу деп аламыз.

Нұсқау. Капиллярдың ішінде қалған су бағанасының шеткі ұзындығы, капиллярдың радиусына тең болатын төменгі менискінің қисықтың радиусына сәйкес болуы керектігін ескеру керек (алдынғы есептің шешуін қараңыздар)

7.70. Ішшкі радиусы r=0.6 мм-ге тең ашық вертикаль қалыптағы капиллярдың ішінде спирт бағанасы бар. Осы спирт бағанасының төменгі менискісі капилярдың төменгі ұшынан түсіп тұрады. Төменгі менискінің қисықтық радиусы: 1) 3r.2 2) 2r және 3) r-ге тең болатын спирт бағанасының h биіктігін табу керек. Толық жұғу деп аламыз.

7.71. 14-суретте көрсетілген түтіктің екі ұшы ашық болып келген де керосимен толтырылған. Түтікшенің ішкі радиусы және в сәикес r =0.5мм және r 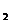=0,9 мм-ге тең. Түтіктің ішіндегі керосин деңгейінің қандай h айырымында, онің ұшындағы менискісі: 1)ойыс, қисықтық радиусы R = r 2) жазық 3) дөңес қисықтық радиусы R = r 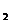4) дөңес және r-ге тең болады. Толық жұғу деп есептейміз.

7.72. Суы бар кең ыдыстың ішіне, жоғарғы ұшы ыдыстағы судың деңгеиінен h=2 см биіктікке тұратындай етіп капилляр батырылған. Капиллярдың ішкі радиусы r=0.5 см-ге тең. Капиллярдағы менискінің қисықтық радиусы R табу керек. Толық жұғу деп есептейміз.

7.73 Ареометр, оның қабырғасына толық жұғылатын судың ішінде жүзеді. Ареометірдіңвертикаль цилиндр түтігінің диаметірі d= 9 мм-ге тең. Егер судың бетіне спирттің бірнеше тамшысын құйсақ,онда ареометірдің судың ішіне бату тереңдігі қаншаға өзгереді?

7.74. Ареометр, тығыздығы p= 800 кг\м және беттік керілу коэффиценті =30 дин \ см сұйықтың ішінде жүзеді. Сұйық ареометрдің қабырғасына толық жұғады. Ареометірдің вертикаль майланудың салдарынан, осы сұйық толық жұқпайтын жағдайға айналды десек, ареометірдің суға бату тереңдігі қаншаға өзгереді?

7.75. 10 г қантты (C H O ) 0,5 л суға еріткен уақытта ерітіндінің осмыстық қысымы 1,52۬ · 10 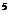н\м 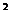-ге тең болады. Ерітінді қандай температурада болады? Қанттың малекулаларының диссоциациясы болған жоқ.

7. 76. 87 С температурада тұрған ерітіндінің осмыстық қысымы 1,65 · 10 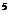н\м 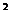-ге тең. Осы ерітіндідегі еріген заттың бір малекуласына судың қанша малекуласы тура келеді?Диссоциация болған жоқ.

7.77. 0,5 л суға 2 г ас тұзы ерітілген. Кесек тұздың молекулаларының диссоциациясының дәрежесі 75 процентке тең. 17 С температурадағы ерітіндінің осмыстық қысымын табу керек.

7.78. Суға еріткендегі ас тұзы малекулаларының дисоциация дәрежесі 40процентке тең. Бұл жағдайда 27 С температурада тұрған ерітіндінің осмыстық қысымы 1,210кг\см 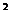-ге тең. 1 л суда ерітілген ас тұзының мөлшері қандй?

7. 79. 18 С температурадаи 1л суға 2,5 г ас тұзы ерітілген. Ерітіндінің осмыстық қысымы 1,6 · 10 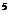н\м 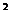-гетең. 1)Осы жағдайда ас тұзы малекулаларының дисоциациялануыдәрежесі қандай. 2) 1см ерітіндінің ішінде еріген заттың қанша бөлшегі болады?

7.80. 40г қант (C H O ) 0,5л суға ерітілген. Ерітіндінің температурасы 50 С –ге тең. Ертіндінің үстіндегі қаныққан су буының қысымы қандай болады?

СВ

7.81. 30 С температурадағы ерітіндінің үстіндегі қаныққан будың серпімділігі 31,5 мм сын. бағ-на тең. Осы ерітіндінің үстіндегі қаныққан будың серпімділігін 60 С температура үшін табу керек.

7,82. Ерітіндінің үстіндегі қаныққан будың серпімділігі 1,02 есе кіші. Ерітілген заттың бір молекуласына су молекулаларының қаншасы тура келеді?

7. 83. Өздігінен ұшып кетпейтін 10г зат 1л суда ерітілген. Ерітіндінің температурасы 90 С-ге тең, ал ерітіндінің үстіндегі қаныққан бу 515,9 мм сын. бағ. қысымында. Ерітілген заттың бір киламолінің массасын табу керек.

7.84. Бір киламольдің =60 кг\кмоль массасы бар өздігінен ұшып кетпейтін зат суды ерітілген. Ерітіндінің температурасы 80 С, ал ерітіндінің үстіндегі қаныққан будың қысымы 353 мм сын. бағ. Ерітіндінің осмыстық табу керек.

Атты денелер

Қысым dp өзгергендегі dT балқу температурасының өзгерісі Қлаузиус — Қлапейрон теңдеуі арқылы беріледі

dT=T

мұндағы qo — балқудың молекулалық жылуы, V_c — сү-йықтың бір киломолінің көлемі, Ғ_қ — қатты дененің бір киломолінің көлемі, Т — балқу температурасы.

Температура аса төмендемеген кезде қатты денелер үшін Дюлонға және Пти заңы тура келеді. Бұл заң бо-йынша барлық химиялық жабайы қатты денелердің атомдық жылу сыйымдылығы шамамен алғанда Зі? = 25«• 10³ дж/кг-атом • град = 6 кал/г-атом • град-қа тең.

Жылу өткізгіштіктің салдарынан Д/ уақыттың ішінде ауысатын жылудың мөлшері мынадай формуламен анық-талынады:

Q=-Y

мұндағы ауданға перпендикуляр болып бағыт-

талған температура градиенті. % — жылу еткізгіштік коэффициенті.

Температураны жоғарылатқанда қатты денелердің ұзындығы бірінші жуықтықта температурамен бірге сызықтық ұлғаяды, яғни

l

мұндағы l_t — t температурадағы дененің ұзындығы, /₀ — оның 0°С температурадағы ұзындығы, ал а— жылу-лық сызықтык ұлғаю коэффициенті.

Изотропты қатты денелер үшін болады, мұн-

дағы b — жылулық көлемдік ұлғаю коэффициенті.

Стерженьді бойлық созу (бір бетті сығылу) деформа-циясы жағдайында стерженьнің ұзындығының салыстыр-малы өзгерісі Гук заңы бойынша мынадай болады,

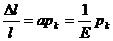
мұндағы р_к — меншікті күш, яғни болады, мүн-

дағы Ғ — созу (сығу) күші, S — кәлденең қиманың ауда-

• ны, ал a—серпімділік коэффициенті. шаманы

серпімділік модулі (Юнга модулі) деп атайды.

Бойлық созылу кезінде стерженьнің қалыңдығының салыстырмалы өзгерісі

мүндағы pt — көлденең сығылу коэффициенті. Мына ша-маны

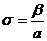
Пуассонның коэффициенті деп атайды.

Стерженьді (сымды) белгілі бір бұрышқа бұру үшін міндетті түрде қос күш моментін түсіру керек:

M=

мұндағы /—сымның үзындығы, г — оның радиусы, ал Л^ — сым материалының ығысу модулі.

8.1. 1 кмоль мүзды еріткендегі энтропияның өзге-рісі 22,2 кдж/град-қа тең. Сыртқы қысымды 1 • 10⁵я/ж²-ге өзгерген кезде мұздың балқу температурасының қаншаға өзгеретінін табу керек.

8.2. 10⁵ н/м² қысымдағы қалайының балқу температу-расы 231,9°С-ге тең, ал 10⁷ н/м² қысымда оның балқу тем-пературасы 232,2°С-ге тең болды. Сұйық күйдегі қалайы-ның тығыздығы 7,0 г\см^ъ. 1 кмоль қалайыны балкыт-қандағы энтропияның есуін табу керек.

8.3. Қысымды 1 кГІсм²-те өзгерткенде, темірдің балқу температурасы 0,012°-қа езгереді. Балқыған кезде бір киломоль темірдің көлемінің каншама өзгеретіндігін табу керек.

8.4. Дюлонга мен Птидің заңын пайдаланып: 1) мыс-тың, 2) темірдіқ, 3) алюминийдің меншікті жылу сыйым-дылығын табу керек.

8.5. Дюлонга мен Птидіқ заңын пайдаланып, ауырлы-ғы 0,025 кГ металл шариктің қандай материалдан жасал-ғандығын табу керек. Осы шарикті 10°С-ден 30°С-ге дейіьгқыздыру үшін 117 дж жылу жүмсалынған.

8.6. Дюлонга мен Птидің заңын пайдаланып алюми-нийдің меншікті жылу сыйымдылығы платинаның жылу сыйымдылығына қарағанда неше есе үлкен болатынды-ғын табу керек.

8.7. 400 м/сек жылдамдықпен үшып келе жатқан қор-ғасын оқ қабырғаға соғылады да, оның ішіне кіріп кете-ді. Оқтың кинетикалық энергиясының 10 процентін оның өзін қыздыруға кетеді деп, оқтың қанша градусқа кыз-ғанын табу керек. Қорғасынның меншікті жылу сыйым-дылығын Дюлонга мен Птидің заңы бойынша табу керек.

8.8. Мыстан (қалыңдығы d\ = 9 mm) және темірден (қалыңдығы (І2=3 мм) жасалынған пластинкалар бірік-тіріліп салынған. Мыс пластинканың сыртқы бетін ^і = 50°С температурада түрақты үстап, ал темір пластинканың сыртқы бетін І2 = 0°С температурада ұстап тұрып олардың бір-біріне тиіскен беттерінің температурасын t_x табу керек. Пластинкалардың беттерінің ауданы олар-дың қалыңдығымен салыстырғанда анағұрлым үлкен. 8.9. Үйдің қабырғасының сыртқы бетінің температу-расы /і = — 20°С, ал ішкі бетінің температурасы /₂ = 20°С. Қабырғаның қалыңдығы 40 см. Қабырғаның әрбір 1 м² бетінен бір сағаттың ішінде 11Q ккал жылу өтеді деп

Гып, оның жылу өткізгіштік коэффициентін табу керек. 8.10. Еденінің ауданы 4X5 м, биіктігі 3 м, қабырғасы төрт кірпіштен каланған бөлме бір минут ішінде қанша жылу мөлшерін жоғалтады? Бөлменің ішіндегі темпера-_Тура /₁ = 15°С, сырттағы температура t₂=— 20°С. Кірпіш-тің жылу өткізгіштік коэффициенті 0,002 кал/град • см • • сек, қабырғаның қалыңдығы 50 см. Белменің едені мен төбесі арқылы кететін жылу шығынын ескермейміз.

8.11. Темір стерженьнің бір ұшы 100°С температурада ұсталып тұрады да, екінші ұшы мұзға тіреледі. Стержень-нің ұзындығы 14 см, келденең қимасының ауданы 2 см². Стерженьді жылу жоғалтпайтындай етіп изоляция-лағаны сондайлық, оның қабырғасы арқылы шыққан жылуды ескермесе де болады. Мыналарды: 1) стержень-нің бойымен өткен жылудың жылдамдығын, 2) 40 мин ішінде еритін мұздың мөлшерін табу керек.

8.12. Егер мыс стерженьнің ұштарындағы температу-ралар айырмасы 15°С болса, онда көлденең қимасының ауданы 10 см², ұзындығы 50 см, стержень арқылы 1 сек ішінде қанша жылудың мөлшері өтеді? Жылу шығында-рын ескермейміз.

8.13. Плитаның үстінде диаметрі 15 см ішіне су тол-тырылған алюминий кастрюль тұр. Су қайнаған уақытта әрбір минут сайын 300 г су буы пайда болып отырады. Кастрюльдің түбінің сыртқы бетінің температурасын та-бу керек. Кастрюльдің түбінің калыңдығы 2 мм-те тең. Жылу шығындарын ескермейміз.

8.14. Радиусы 9 см металл цилиндр ыдыс 0°С темпе-ратурада мүзбен толтырылған. Ыдыс жылу өткізбейтін-дей етіп қалыңдығы 1 см пробкамен жабылған. Егер сырттағы ауаның температурасы 25°С-ге тең болса, онда ыдыстың ішіндегі мүз қанша уақыттан кейін түгелімен

ериді? Жылудың ауысуы тек қана радиусы 9,5 см-те тең ыдыстыц бүйір беті арқылы өтеді деп есептейміз.

8.15. Көлденеқ қимасының ауданы S=10 см² болат стерженьді /і = 0°С-ден /₂ = 30°С-ге дейін қыздырғанда үлғаюыпа мүмкіндік бермеу үшін, оның үштарына түсірі-летін күштер қандай болу керек?

8.16. Радиусы 1 мм болат сымға жүк ілінген. Осы жүктің әсерінен сым, оны 20°С қыздырғандағыдай қо-сымша үзындық алады. Жүктің шамасын табу керек?

8.17. І50°С температурадағы мыс сымы ыстық күйінде қозғалмайтын берік екі кабырғаның арасына керіп қо-йылған. Сым суи келе, қандай температурада үзіліп ке-теді? Гуктың заңыи сым үзіліп кеткенге дейін қолдануға болады деп есептейміз.

8.18. Кейбір металды 0-ден 500°С-ге дейін қыздырған-да, опың тығыздығы 1,027 есе кемиді. Осы металл үшін жылулық сызықтық үлғаю коэффициентін табу керек. Оны берілген температура интервалында тұрақты деп ал4^иыз.

^ 8.19. Қез келген температурада болат стерженьнің үзындығы мыс стерженьнің ұзындығынан 5 см үзын болу үшін осы болат және мыс стерженьдерінін, 0°С-де үзын-дықтары қаыдай болу керек?

8.20. Салмағы 1 кГ 0°С температурадағы мыс собықты (болванканы) қыздыру үшін 33 ккал жылу жүмсалынды. Осы уақытта оның көлемі неше есе үлкейеді? Мыстың жылу сыйымдылығын Дюлонға және Пти заңы бойынша табыңдар.

8.21. Қөлденең қимасы 1,5 мм²-ге тең мыс сымын соз-ғанда қалдық деформацияның басталуы 4,5 кГ күш түсіргенде байқалды. Сым материалының серпімділігі-нің шегі қандай болады?

8.22. 1 Т күш түскенде үзіліп кетпей төтеп беретін бо-лат тростың шекті диаметрі қандай болу керек?

8.23. Вертикаль қалпында ілгенде өзінің меншікхі сал-мағының әсерінен үзіліп кететін мыс сымының ұзындығын табу керек?

8.24. Осыныд алдындағы есепті қорғасын сым үшін шешіңіздер.

8.25. Теңіздің тереңдігін өлшеу үшін пароходтан болат арқанмен (трос) гир түсірілген. Арқанның салмағына қарағанда гирдің салмағын есепке алмай, осы тәсілмен ең тереңдікті қалай өлшеуге болатындығын табу керек. Теңіз суының тығыздығын 1 г/см³-те тең деп аламыз.

8.26. Үйдің шатырынан үзындығы 40 м, ал диаметрі 2 мм болат сым түсірілген. 1) Осы сым үзілмес үшін оған салмағы қандай жүк ілу керек? 2) Егер осы сымға сал-мағы 70 кГ адам асылып тұрса, онда сым қаншаға үзара-ды? 3) Адам сымды босатып жіберген уақытта калдық деформация байқала ма? Болаттың серпімділік шегін 2,94 • 10⁸ н/м²-те тең деп аламыз.

8.27. Радиусы 1 мм болат сымға 981 н жүк ілінген. Осы тепе-теңдік қалыптан өткен уақытта үзіліп кетпеу үшін сымды жүгімен бірге қандай ең үлкен бұрышқа бұру керек? /

8.2ЙУ Үзындығы 50 см, диаметрі '1 мм темір сымға салмағы 1 кГ гир ілінген. Осы жүгі бар сымды вертикаль жазықтықта бір қалыпты айналдырғанда ол үзіліп кет-пеу үшін бір секунд ішіндегі ең көп айналым саны қандай болу керек?

Не нашли, что искали? Воспользуйтесь поиском: