Преломление на сферической поверхности

Рассмотрим теперь преломление на сферической поверхности радиуса R с центром в точке O. Рассмотрим несколько случаев.

Случай 1 (рис. 12)

Пусть точечный источник света находится на расстоянии d от поверхности стекла (показатель преломления которого n >1). Докажем, что различные лучи, выходящие от источника S под малыми углами к прямой SO, пересекаются в одной точке. Для этого рассмотрим преломление произвольного луча SB, составляющего с осью малый угол a. Перпендикуляром к поверхности в точке В служит радиус ОВ, составляющий с осью угол g. Обозначим через i угол падения, а через r – угол преломления. Преломленный луч пересекает ось в точке S'. Преломленный луч BS' составляет с осью угол a'.

Найдем соотношение между расстояниями SP = d, S'P = f и ОР = R. Учтем, что при малом угле a отрезок PD также мал и им можно пренебречь по сравнению с расстояниями SP, S'P и ОР. Тогда d» SD, f» S'P, R» OD. Из треугольников SBD, S'BD и OBD можно получить следующие равенства

tg a» h / d, tg a'» h / f и tg g» h / R.

Если угол a мал, то малы и углы g и a', и их тангенсы можно заменить значениями самих углов в радианах:

a» h / d, a'» h / f; g» h / R.

Чтобы выяснить, как связаны между собой d, f и R, найдем, как связаны между собой углы a, a' и g. Угол i является внешним углом треугольника SBO. Поэтому

i = a + g.

Угол g – внешний угол треугольника OBS'. Следовательно,

g = r + a' Þ r = g – a'.

Т.к. углы малы, то в законе преломления синусы углов можно заменить самими углами: n = sin i /sin r» i / r. Отсюда

i» r × n.

Выразим i и r в уравнении через приосевые углы:

a + g = (g – a') n, a + a'n = g (n – 1).

Подставляя в выражения и сделав преобразования, получим:

.

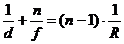В это соотношение не входит h; существенно лишь, чтобы h было мало. Это означает, что все приосевые лучи пересекаются в одной точке S', которая является изображением S. Выражение называют нулевым инвариантом Аббе.

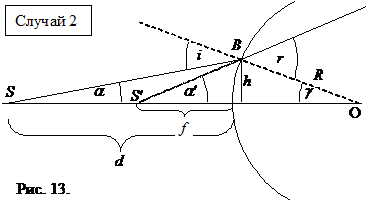
Случай 2 (рис. 13)

Пусть теперь показатель преломления слева от сферической поверхности больше, чем показатель преломления справа от нее.

Рассмотрим, как на поверхности преломляется луч SB, идущий из точки S, которая сама находится в среде с показателем преломления n >1 (луч, таким образом, выходит из этой среды в точке B). Если продолжить преломленный луч влево от точки B, то точка его пересечения с прямой SO дает мнимое изображение S ¢. Мнимое потому, что реального пересечения лучей там нет. Наблюдателю же справа видимое расстояние f до источника будет казаться меньше, чем реальное d. Найдем, как связаны f и d.

Во-первых, формулы имеют место и в этом случае. Далее, т.к. угол i – внешний по отношению к треугольнику SBO, то

i = a + g» h / d + h / R.

Аналогично, для треугольника S ¢ BO

r = g + a ¢.

Вычитаем r из i:

i – r = a – a ¢» h / d – h / f.

Но r» ni, поэтому i – r = (1 – n) i, что с учетом и дает

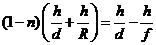, или .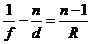

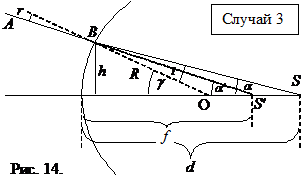Случай 3 (рис. 14)

Рассмотрим ту же ситуацию, что и в предыдущем случае, только с источником света S, находящимся справа от поверхности. Продлевая преломленный луч AB вправо, мы снова получаем мнимое изображение S ¢ на расстоянии f от поверхности. При этом снова остаются справедливыми выражения.

Угол g является внешним по отношению к треугольникам OBS и OBS ¢. Значит,

g = i + a и g = r + a ¢,

откуда следует, что

i = g – a = h / R – h / d,

i – r = a ¢– a = h / f – h / d.

По закону преломления r» i / n, т.е. i – r = (1 – 1/ n) i. Приравнивая это к и подставляя i из, получим

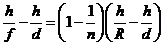, или .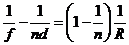

Не нашли, что искали? Воспользуйтесь поиском: