ЛАБОРАТОРНАЯ РАБОТА №3. Дифракция Фраунгофера

Дифракция Фраунгофера

Краткая теория. Вблизи краев отверстий или экранов фронт волны искажается, вследствие чего изменяется направление волнового вектора. Отклонение световых лучей от прямолинейного пути при прохождении света вблизи краев экрана, отверстий (или других неоднородностей) называется дифракцией. Если дифрагированные волны являются когерентными, то дифракция сопровождается интерференционными явлениями.

Различают два вида дифракции: дифракция Френеля (когда Q/(в l)~1, Q - площадь волнового фронта, который пропускается отверстием или перекрывается диском, в - расстояние до точки наблюдения от препятствия, l - длина волны) и дифракция Фраунгофера (когда Q/(в l)<<1).

	Если источник света и точка наблюдения находятся от препятствия достаточно далеко, так что можно считать падающие и дифрагированные волны плоскими, то в этом случае имеет место дифракция Фраунгофера. Все остальные случаи дифракции относятся к дифракции Френеля.
рис. 1

В данной работе изучается дифракция Фраунгофера на одной и двух щелях и на дифракционной решетке.

Дифракция на щели. Если на щель шириной а перпендикулярно падает параллельный пучок света (рис.1), то от элементарного участка щели шириной dx в направлении ВА, которое определяется углом j, распространяется волна напряженностью электрического поля dЕ _j; амплитуда этой волны равна Cdx, фаза -(w t - kx sinj):

dE _j= Cdx cos( w t-kx sinj), (1)

где С - постоянная, k - волновое число.

После интегрирования по ширине щели получим уравнение волны, распространяющейся по направлению j:

(2)

амплитуда ее:

(3)

где Е ₀ - амплитуда волны, распространяющейся в направлении j =0.

рис. 2

Направления, в которых интенсивность дифрагированных волн равна нулю вследствие их интерференции, определяются согласно (3)

условием:

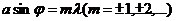(4)

Между минимумами расположены максимумы, которые определяются из условия¶ E _j0/¶ j=0.

	Из этого условия следует, что максимумы при дифракции плоских волн на одной щели определяются соотношением: (5) Графически зависимость 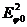от sinj представлена на рис.2 утолщенной линией.
рис. 3

Дифракция на параллельных щелях. Система одинаковых параллельных щелей, которые расположены в одной плоскости на одинаковом расстоянии друг от друга, называется дифракционной решеткой. Рассмотрим дифракцию плоских волн, которые падают нормально к плоскости решетки (рис.3 ). Разность фаз результирующих волн (например, 1 и 2), проходящих через две ближайшие щели:

(6)

где a - ширина щели, в - промежуток между щелями.

Результирующая напряженность, которая создается волнами, распространяющимися в направлении j от всех щелей, равна:

, (7)

где N - число щелей, напряженности дифрагированных волн, проходящих через отдельные щели; их амплитуды определяются выражением (3). Векторную сумму (7) можно заменить арифметической, если направления колебания векторов одинаковы. Для одинаковых щелей амплитуды напряженностей будут равны Е _j0. Тогда:

(8)

	Сумму, входящую в (8), можно рассчитать методом фазовых диаграмм, Согласно этого метода модули векторов изображаются отрезками, как показано на рис.4. Направления соседних отрезков отличаются друг от друга на угол g; таким образом учитывается различие в начальных фазах. Амплитуда результирующей волны будет равна отрезку AN; рассчитаем его значение. Угол АОЕ 1=g; угол АON=N g, АО = R.   (9)
рис. 4

После замены E_j0 из соотношения (3) получается выражение для амплитуды напряженности результирующей волны, распространяющейся после дифракции на решетке в направлении j:

. (10)

Из анализа выражения (10) можно сделать следующие выводы.

1.Интенсивность дифрагированных на решетке волн определяется произведением двух функций:

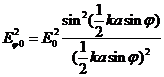, (11)

. (12)

2.Главные минимумы определяются соотношением:

a sinj =ml (m= ±1, ±2,...); (13)

оно справедливо для любого числа щелей.

3.Главные максимумы определяются соотношением:

sin(g/2)= 0, т.е. (a+в) sinj =ml (m= 0, ±1,...). (14)

4.Дополнительные минимумы определяются соотношениями:

sin(Ng /2)= 0, sin(g /2)¹ 0, т.е. (a+в) sinj =m’ , (15)

(m’ - целые числа, не кратные N).

Число дополнительных минимумов между двумя ближайшими главными максимумами равно (N -1). В результате интерференции дифрагированных волн поток распределяется, в основном вблизи направлений, соответствующих главным максимумам.

Распределение интенсивности электромагнитных волн для трех щелей графически показано на рис.2. По оси абсцисс отложены значения sinj, по оси ординат отложены значения функций относительно их максимальных значений; функция 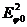представлена утолщенной линией, функция Ф ² показана штриховой линией (только слева от оси ординат).

Распределение потока соответствует дифракции на трех щелях (N =3) при условии в = 3 a.

Не нашли, что искали? Воспользуйтесь поиском: