Преломление на сферической границе.

ходу луча— со знаком плюс; отрезки, которые откладываются по перпендикуляру к оптической оси вверх, записываются со знаком плюс, вниз — со знаком минус; углы отсчитываются от оптической оси S₁S₂, углы падения и преломления — от нормали; если отсчёт идёт по часовой стрелке, то угол записывается со знаком плюс, против часовой стрелки — со знаком минус. Из чертежа видно, что: , g= -r₁+u₂, , , На основании закона преломления для параксиальных лучей: n₁i₁=n₂r₁, n₁(u₁-g)=n₂(u₂-g) или

(1)

Tочки S₁ и S₂, являющиеся центрами гомоцентрических пучков, которые преобразуются этой системой, называются сопряжёнными точками. Соотношение (1) называется уравнением сопряжённых точек. Величина называется оптической силой сферической поверхности.

материала, которое ограничено двумя сферическими поверхностями. Такие линзы имеют ось симметрии, которая называется главной оптической осью. Линзу будем рассматривать как идеальную оптическую систему. Идеальная оптическая система дает изображение точечного источника в виде точки. Достаточно хорошим приближением идеальной оптической системы может быть центрированная система, если на неё падают параксиальные пучки.

рис.2

Оптическая сила линзы. Линзой называется тело из прозрачного

В дальнейшем рассматриваются только идеальные оптические системы.

Построим ход луча, который направлен параллельно главной оптической оси О₁О₁ (рис.2). Среда по обе стороны линзы одинакова (показатель преломления n₁). Толщина линзы d, показатель преломления стекла линзы n₂. Точка F₂, в которой лучи, падающие параллельно главной оптической оси, пересекают оптическую ось, называется фокусом. Применим уравнение (1) к сферическим поверхностям I, II, а затем к линзе в целом. Обозначим оптические силы соответственно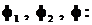

-n₁u₁+n₂u₂= f₁ h_1, (2)

-n₂u₂+n₁u₃= f ₂h_2, (3)

-n₁u₁+n₁u₃= f h₁ (4)

Учитывая, что:

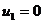и (5)

получим:

(6)

Для тонкой линзы (d << R),

f=f₁+f₂. (7)

Кардинальные точки и плоскости оптической системы. Направим луч 1 параллельно оптической оси (рис. 3). Продолжим его до пересечения с продолжением луча, проходящего через фокус F₂, получим точку К₂. Навстречу лучу 1 направим луч 2. Получим точку К₁. Проведём через эти точки плоскости перпендикулярно главной оптической оси.

	Такие плоскости называются главными плоскостями, а точки H1 и H2 — главными точками. Главные плоскости являются геометрическим местом сопряжённых точек, которые расположены на одинаковых расстояниях от оптической оси и находятся по одну сторону от неё. Эта пара плоскостей и точек относится к основным
рис.3

(кардинальным) элементам любой идеальной оптической системы.

Расположение главных точек относительно оптических центров сферических поверхностей линзы определяется отрезками x₁ и x₂.

Из рис.3 следует:

.

Учитывая (2), (4), (5), получим:

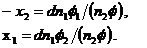(8), (9)

Второй парой кардинальных элементов являются фокусы F₁ и F₂ и фокальные плоскости, которые проходят через фокусы перпендикулярно оптической оси. Фокус F₂, расположенный в пространстве изображений, называется задним фокусом, фокус F₁, расположенный в пространстве предметов, называется передним фокусом. Фокус является сопряжённой точкой для бесконечно удалённой точки. Расстояние от главной точки до фокуса называется фокусным расстоянием (f).

Фокусное расстояние связано простым соотношением с оптической силой. Из рис. 3 следует:

h₁/f₂=u₃ (10)

Учитывая (4) (при условии u₁=0), получим:

ff₂ = n₁ (11)

ff₁ = -n₁. (12)

Если фокусное расстояние выражается в метрах, то оптическая сила выражается в диоптриях. Оптическая система имеет положительную оптическую силу, если передний фокус её F₁ лежит левее точки Н₁, а задний фокус F₂ — правее точки Н₂ (предполагается, что свет распространяется слева направо).

Третьей парой кардинальных элементов являются узловые точки, которые обладают тем свойством, что луч (или его продолжение), входящий в линзу через одну узловую точку, при выходе из неё пройдёт через другую узловую точку под таким же углом (по значению и знаку) к главной оптической оси. Плоскости, проходящие через узловые точки перпендикулярно главной оптической оси, называются узловыми.

Если среда по обе стороны линзы одинакова, узловые и главные плоскости совпадают.

Уравнение линзы. Построим изображение в линзе (рис. 4). Расположение фокусов и главных точек указано на чертеже. Отсчёт расстояний производится от соответствующих главных плоскостей с учётом правила знаков. Из подобия треугольников А₂В₂С₂ и F₂Н₂С₂ следует:

; (13)

из подобия треугольников А₁В₁С₁ и F₁Н₁С₁:

. (14)

Из (13) и (14) следует:

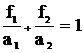. (15)

Это уравнение сопряжённых точек линзы. Когда среда по обе стороны линзы одинакова, то -f₁=f₂=f, тогда уравнение (15) можно записать в виде:

. (16)

При расчёте по (16) значение f подставляется со знаком плюс, если линза имеет положительную оптическую силу; в противном случае f подставляется со знаком минус.

рис. 4

Для тонкой линзы обе главные плоскости совпадают и проходят через её оптический центр; поэтому a₁, a₂, f₁, f₂ отсчитываются от оптического центра линзы.

Экспериментальная установка и измерения. Для определения фокусных расстояний используется оптическая скамья, на которой с помощью рейтеров устанавливаются освещённое матовое стекло с прямоугольной сеткой, белый экран и соответствующие линзы.

Работа 4а

Не нашли, что искали? Воспользуйтесь поиском: