ЛАБОРАТОРНАЯ РАБОТА №7. Краткая теория. Дисперсией называется зависимость показателя преломления (или фазовой скорости распространения волн) от длины волны l

Дисперсия призмы

Краткая теория. Дисперсией называется зависимость показателя преломления (или фазовой скорости распространения волн) от длины волны l. Мерой дисперсии является производная ¶ n /¶l, равная изменению показателя преломления при изменении длины волны на единичный интервал. Если ¶ n /¶l<0, то дисперсия называется нормальной; если ¶ n /¶l>0, то дисперсия называется аномальной.

В области нормальной дисперсии зависимость показателя преломления n от длины волны может быть представлена формулой Коши с эмпирическими коэффициентами A, В, С:

n = A + B / l ²+ C / l ⁴+… (1)

где l - длина волны в вакууме; или формулой Лоренц-Лоренца:

A’r =(n ²-1)/(n ²+2), (2)

где A’ - константа, r - плотность.

Дисперсия объясняется электронной теорией как результат взаимодействия проходящей через вещество электромагнитной волны с электронами.

Под действием проходящих электромагнитных волн электроны совершают вынужденные колебания, вследствие чего излучаются вторичные электромагнитные волны с той же частотой. Амплитуда и фаза вторичных волн зависит от соотношения между частотой первичных волн w и частотой собственных колебаний электронов w₀.

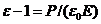Вынуждающая сила при распространении гармонической волны: (q - заряд электрона); действие магнитного поля будет мало: q V m ₀ H /(qE)=V/ c <<1. В результате смещения электронов среда будет поляризоваться; вектор смещения ( - вектор поляризации); , следовательно . Если электрон смещается на , то электрический момент ; если все электроны смещаются в одном направлении и на одинаковую величину , то модуль вектора поляризации P=Nqr (N - число сместившихся электронов в единичном объеме).

Уравнение движения электрона массой m под действием вынуждающей силы с учетом действия на него квазиупругой силы и силы трения , пропорциональной скорости смещения :

. (3)

В этом выражении гармоническая функция соs (wt - kx) представлена множителем e^iwt (при x =0).

Решение находится в виде r = r ₀ e^iwt; после подстановки его в (3) получим: .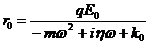

Введем обозначения w²₀= k ₀/ m, g=h/ m, ; модуль

,

. (4)

рис. 1

График этой функции приведен на рис. 1. На участке АВ n увеличивается с увеличением частоты; это область нормальной дисперсии. Участок ВС соответствует аномальной дисперсии. Участок СD соответствует (как и участок АВ) области нормальной дисперсии, но на этом участке n <1. Это наблюдается в области высоких частот, когда w>w₀ (w₀ - собственная частота колебаний электронов).

Если r ₀ величина комплексная, то e*, n *, k * также будут комплексные. Пусть k *= k - i a, тогда e^{i( w t-k*x)} = e^{i (w t - kx ).} e ^{-a x}, т.е. электромагнитная волна затухает (коэффициент поглощения a).

При малых поглощениях (когда gw/ m <<w₀²-w²) показатель преломления определяется выражением:

. (5)

В общем случае может быть несколько резонансных частот и соответствующих им полос аномальной дисперсии.

Если w<<w₀, то из (3) получается выражение, аналогичное формуле Коши (1):

, (6)

где , , с - скорость света.

Расчет по соотношению (6), строго говоря, применим лишь для разреженных газов или для веществ, в которых концентрация диполей мала, поэтому полученные для стекла значения A ₀ и B ₀ следует рассматривать как ориентировочные.

Квантовой теорией дисперсия объясняется на основе учета переходов электронов между дискретными энергетическими уровнями энергии под действием падающего света. Собственные частоты колебаний электронов представляют частоты квантовых переходов атомов или молекул с самых низких уровней. Запаздывание по фазе вторичного излучения в квантовой теории эквивалентно увеличению продолжительности жизни атома в возбужденном состоянии.

Не нашли, что искали? Воспользуйтесь поиском: