
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Математическая модель
Пусть Xij тип судна производительность на линиях (i=1…3,j=1…3)

Зная, заданный оббьем перевозок 300, 5400, 3300 (млн. т. миль), то можно записать систему ограничений.

Z=8  +14
+14  +11
+11 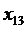 +6
+6 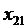 +15
+15  +13
+13  +12
+12  +12
+12  +4
+4 
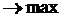
Решение задачи сводится к нахождению отрицательных значений неизвестных xij выражающих, чтобы обеспечить максимальную загрузку судов с учетом возможного времени их эксплуатации.
В данной задачи сумма заданного объема перевозок равна с суммой с общим временем эксплуатации:
300+5400+3300=300+300+300+10800  следовательно, это транспортная задача с закрытой моделью.
следовательно, это транспортная задача с закрытой моделью.
1. Поиск допустимого решения.
Первый опорный план для решения задачи составим методом северо-западного угла (Табл.1). Особенность этого метода в том, что распределение начинается с левой верхней клетки, так, как сумма значений по строкам равна сумме значений по строкам
| Магазины Склады | Запасы в пунктах отправления | ||||
| Vj Ui | |||||
  X11 X11
|
 X12 X12
| X13 | |||
| -2 | - 6 X21 | +15 X22 | X23 | ||
| X31 | X32 | X33 | |||
| -8 | + 0
 2100
X41 2100
X41
| -0 X42 | X43 | ||
| Заданный объем перевозок (млн. т.миль) |
Таблица 1.
l12= 14-8 =6
l13= 11-8 =-32
l22=15-(8-2) =9
l23= 13-(8-2) =7
l32= 12-(8+4) =0
l33= 4-(8+4) =-8
Таким образом, общее время распределено и весь заданный обьем удовлетворен. Получен первый допустимый план при следующих значениях неизвестных
X11 =300; X21=300; X31=5400; X41=2100; X42=5400; X43=330.
Значения остальных неизвестных равно нулю. Значение целевой функции при этом равно:
Z1 =300*8+300*6+300*12=7800
Для проверки правильности распределения ресурсов и удовлетворения потребностей необходимо суммировать объем перевозок, как по строкам, так и по столбцам. После этого план проверяется на оптимальность.
Условимся называть клетки матрицы, соответствующие положительным компонентам плана, занятыми (базисными), а остальные – свободными (небазисными). Число занятых клеток в опорном плане должно быть m+n+1. В случае, когда их оказывается меньше, одну из свободных клеток условно считают занятой и проставляют в ней перевозки xij =0. При этом надо следить за тем, чтобы условно занятая не образовывала с другими клетками замкнутых контуров.
Не нашли, что искали? Воспользуйтесь поиском: