
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Решение систем уравнений матричным методом. Система уравнений может быть записана в виде
Система уравнений 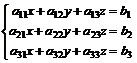 может быть записана в виде
может быть записана в виде
АХ = В, где А = 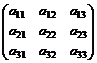 , Х =
, Х = 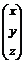 , В =
, В = 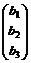 .
.
Решение этой системы имеет вид: Х =А-1 В (если 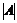 ¹ 0).
¹ 0).
Пример. Решить систему  , представив ее в виде матричного уравнения.
, представив ее в виде матричного уравнения.
Решение: Перепишем систему в виде АХ = В.
А = 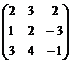 , Х =
, Х = 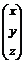 , В =
, В = 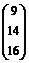 .
.
Решение матричного уравнения имеет вид: Х =А-1 В. Найдем А-1:
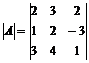 = -6.
= -6.
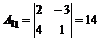 ;
; 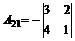 = 5;
= 5; 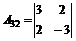 = -13
= -13
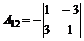 = -10;
= -10; 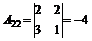 ;
; 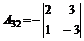 = 8
= 8
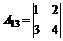 = -2;
= -2; 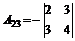 = 1;
= 1; 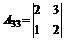 = 1
= 1
Откуда
Х =  ,
,
следовательно, х = 2, y = 3, z = -2.
Ранг матрицы.
Дана прямоугольная матрица
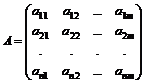
Выделим в этой матрице k произвольных строк и k произвольных столбцов (k 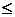 т,
т,
k 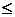 n). Определитель k- го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называем минором k-го порядка матрицы А. Рассмотрим всевозможные миноры матрицы А. Рангом матрицы А называется наибольший порядок минора этой матрицы, отличный от нуля. Если все элементы матрицы равны нулю, то ранг этой принимают равным нулю.
n). Определитель k- го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называем минором k-го порядка матрицы А. Рассмотрим всевозможные миноры матрицы А. Рангом матрицы А называется наибольший порядок минора этой матрицы, отличный от нуля. Если все элементы матрицы равны нулю, то ранг этой принимают равным нулю.
Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы.
Ранг матрицы А будем обозначать через Dk (А). Если Dk (А)=Dk (В), то матрицы А и В называются эквивалентными. Ранг матрицы не изменяется от элементарных преобразований. Под элементарными преобразованиями понимают:
1) замену строк столбцами, а столбцов - соответствующими строками;
2) перестановку строк матрицы;
3) вычерчивание строки, все элементы которой равны нулю;
4) умножение какой-либо строки на число, отличное от нуля;
5) прибавление к элементам одной строки соответствующих элементов другой строки.
Пример. Определить ранг матрицы:  .
.
Решение: Все миноры второго и третьего порядков данной матрицы равны нулю, т.к. элементы строк этих миноров пропорциональны. Миноры же первого порядка (сами элементы матриц) отличен от нуля. Следовательно, ранг матрицы равен 1.
Практически удобно пользоваться следующим приемом: если найден минор k - го порядка Dk, то остается вычислить только те миноры (k +1)го порядка, которые представляют собой «окаймление» Dk.
Пример. Определить ранг матрицы: А = 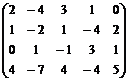 .
.
D2 = 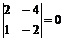 ; D2 =
; D2 = 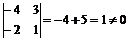 .
.
Не нашли, что искали? Воспользуйтесь поиском: