I. ЛИНЕЙНАЯ АЛГЕБРА. Прямоугольная таблица чисел

Матрицы

Прямоугольная таблица чисел

состоящая из т строк и п столбцов, называется матрицей размера n×m. Числа а₁₁, а₁₂,..., а_mn называются ее элементами. Таблицу, обозначающую матрицу, записывают в круглых скобках и обозначают А = (а_ij).

Если число строк матрицы равно числу ее столбцов, то матрица называется квадратной, а число ее строк, равное числу столбцов, - порядком квадратной матрицы.

Множество всех элементов квадратной матрицы, кото­рые лежат на отрезке, соединяющем левый верхний угол с правым нижним, называется главной диагональю, а на отрезке, соединяющем правый верхний угол с левым нижним - побочной диагональю.

Квадратная матрица называется диагональной, если все ее элементы, не лежащие на главной диагонали, равны нулю. Квадратная матрица, у которой элементы, стоящие по главной диагонали равны единице, а остальные – нули, называется единичной и обозначается Е.

Две матрицы и называются равными, если число их строк и столбцов равны и если равны элементы, стоящие на соответственных местах этих мат­риц.

Матрица, все элементы которой равны нулю, назы­вается нулевой и обозначается через Н.

По определению, чтобы умножить матрицу А на число r, нужно каждый элемент матрицы А умножить на r.

Пример. Дана матрица А = , найти матрицу 3 А.

Решение:

3 А = 3 =

Суммой матриц А и В называется матрица С, элементы которой равны суммам соответственных элементов матриц А и В. Складывать можно только матрицы с одинаковым числом строк и столбцов.

Пример. Даны матрицы А = 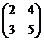и В = . Найти матрицу С = А + В.

Решение:

С =

Свойства сложения матриц:

1) А+В=В+А

2) (А+ В) + С = А+ (В + С)

3) А + Н = А

Произведение матрицы А на матрицу В определено только в том случае, когда число столбцов матрицы А равно числу строк матрицы В. В результате умножения получится матрица АВ, у которой столько же строк, сколько их в матрице А, и столько же столбцов, сколько их в матрице В.

Произведением двух матриц А (m×p) и В (p×n) называется матрица С (m×n), элементы которой определены по правилу

С_ij =

Замечание. Для того, чтобы перемножить две матрицы нужно элементы i -ой строки первой матрицы умножить на элементы j -ого столбца второй матрицы и сложить полученные произведения. Получим элемент новой матрицы с индексом ij.

Не нашли, что искали? Воспользуйтесь поиском: