Прямоугольные координаты. Если в пространстве задана прямоугольная система координат Оxyz, то точка М пространства, имеющая координаты x (абсцисса)

Если в пространстве задана прямоугольная система координат Оxyz, то точка М пространства, имеющая координаты x (абсцисса), y (ордината), z (аппликата), обозначается М (x, y, z).

Расстояние между двумя точками А (х₁, у_1, z₁) и В (х₂ , у_2, z₂) определяется по формуле . В частности, расстояние от точки М (x, y, z) от начала координат О определяется по формуле

Если х₁, у_1, z₁ -координаты точки А, а х_2, у_2, z₂ - коорди­наты точки В, то координаты х и у точки С, делящей отрезок АВ в отношении определяются по формулам

; ;

Если λ == 1, то точка С(х, у,z) делит отрезок АВ пополам, и тогда координаты х и у средины отрезка А В определятся по формулам

; ;

Площадь треугольника на плоскости по известным координатам его вер­шин А (х₁, у₁), В(х₂, y₂), С (х₃, у₃) вычисляется по формуле . Полученное с помощью этой формулы число следует взять по абсолютной величине. Если S = 0, то значит три точки лежат на одной прямой.

Пример. Найти координаты точки С—средины отрезка, соединяющего точки

А (—2, 4) и В (—4, 10).

Решение. В формулах и возьмем х ₁ = - 2; х ₂ = - 4;

у ₁= 4; = 10. Тогда абсцисса средины отрезка АВ х =- 3; ордината - у= 7.

Пример. Найти площадь треугольника, вершины которого находятся в точках А (2, - 3), В (1, 1), С(- 6, 5).

Решение: Задачу решим, воспользовавшись формулой площади треугольника

= 12

Ответ. S = 12 кв. ед.

Скалярное произведение.

Скалярным произведением двух векторов 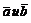называет­ся число, равное произведению их модулей на косинус угла φ между ними. Скалярное произведение векторов обозначается сим­волом .

= cosφ.

Свойства скалярного произведения:

1. = (переместительный закон)

2. = 0, если (скалярное произведение двух перпендикулярных векторов равно нулю) или какой-либо из перемножаемых векторов является нулевым.

3.

4. (распределительный закон)

Скалярное произведение ортов осей координат:

Если векторы заданы своими координатами: , то их скалярное произведение вычисляется по формуле = x₁x₂ +y₁y₂+z₁z₂.

Векторное произведение.

Векторным произведением векторов 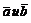называется век­тор , который определяется следующими условиями:

1) Его модуль равен sinφ, где φ - угол между вектора­ми .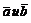

Модуль вектора равен площади параллелограмма, построенного на векторах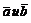

3) ^

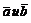
Основные свойства векторного произведения:

1) Векторное произведение равно нулю, если векторы 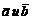коллинеарны или какой-либо из перемножаемых векторов является нулевым.

2) При перестановке местами векторов сомножителей вектор­ное произведение меняет знак на противоположный = ;

3)()´ = (распределительное свойство)

Если векторы 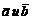заданы своими координатами: , то векторное произведение находим по формуле:

=

Площадь параллелограмма и треугольника, построенного на векторах 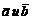, соответственно равны ,

Смешанное произведение

Векторно-скалярное произведение трех векторов или смешанное их произведение вычисляется по формуле

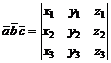, если векторы заданы своими координатами: .

Абсолютная величина смешанного произведения равна объему параллелепипеда, построенного на векторах .

Объем пирамиды, построенной на векторах , получим по формуле причем знак перед определителем должен быть выбран так, чтобы объем V был положительным.

Три вектора называются компланарными, если они лежат в одной плоскости или параллельны одной и той же плоскости. Для того, чтобы три вектора были компланарны, не­обходимо и достаточно, чтобы их смешанное произведение было равно нулю.

Пример. Начти объем пирамиды, если координаты ее вершин А (х₁, у_1, z₁) и В (х₂ , у_2, z₂)

Решение: Рассмотрим векторы , на ко­торых построена пирамида.

Зная координаты начала и конца каждого вектора, найдем проекции этих векторов на оси прямоугольной системы коорди­нат:

, , для объема пирамиды получаем на основании формулы

Не нашли, что искали? Воспользуйтесь поиском: